如果已经学过高数,但是并不是很清楚到底学了什么
我觉得这篇文章可能会有帮助
有一辆公交车,可能会在一点到两点之间到达站点,且在其中每一时刻到达的概率都是相同的。那么在1点30分这一时刻,公交车到达的概率是多少?
假设这个概率不是零,那么在一点到两点之间会有无穷个这样的时刻,这些时刻加起来的概率之和将趋于无穷大,矛盾。但如果这个概率是零,这件事又明明是可能发生的,与常识相悖。
为了解决这个问题,可以创造一个概念:无穷小。即公交车到达的概率是无穷小的。无穷小是0,又不是0。当我们站在时段的角度去观察,它是零,当我们站在时刻的角度去观察,它不是零。
“无穷”的产生,源于观察世界的尺度
微积分是研究这种尺度问题的工具,是处理“无穷”的工具
在讲解积分的时候,经常会提到一个例子:求解曲边梯形的面积
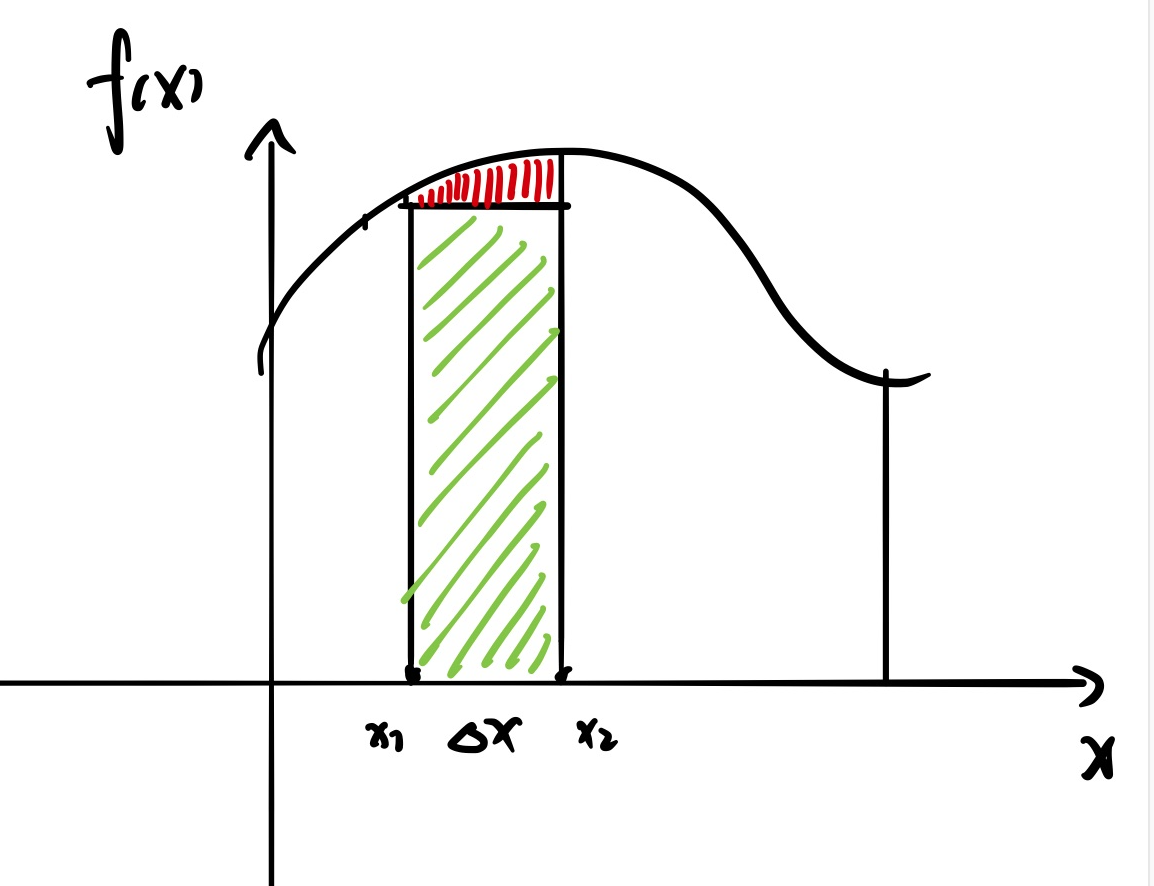
思路是将曲边梯形细分成若干小的曲边梯形,然后用矩形来代替每一个小曲边梯形的面积。如果分的足够细,那么这些矩形面积之和就是曲边梯形面积
这里有一个问题:凭什么矩形的面积可以替代小曲边梯形的面积?
如上图,将每个小曲边梯形分成绿色(矩形部分)和红色(除矩形外的其他部分)两个部分
如果矩形的面积可以替代这个小曲边梯形的面积,说明红色部分的面积S可以忽略
显然红色部分面积满足:
在整个积分区域中,这样的小曲边梯形有$\frac{a-b}{\Delta x}$ 个,所以小曲边梯形的红色面积之和满足: $$ {algin} 0 \le \sum S \le max(|f(x_1)-f(x_2)|) \Delta x *\frac{a-b}{\Delta x} $$ 如果$$\Delta x$$无限趋向于0的过程中,$$f(x_1)$$ 趋向于$$f(x_2)$$,即$$f(x)$$是连续的,则所有小曲边梯形的红色面积之和为零
可以看到,虽然在$$\Delta x$$趋于零的过程中,绿色面积和红色面积都趋于零,但是红色面积趋于零的速度更快。相对于绿色面积来说,红色面积微不足道。红色面积和绿色面积并不在同一尺度上,用微积分语言来说,红色面积是绿色面积的无穷小
假设一个函数F,满足$$F'(x)= f(x)$$,即F是f的不定积分
则F在某个区间[a,b]里的增量,可以由f的定积分$$\int_a^b f(x)dx$$来表示
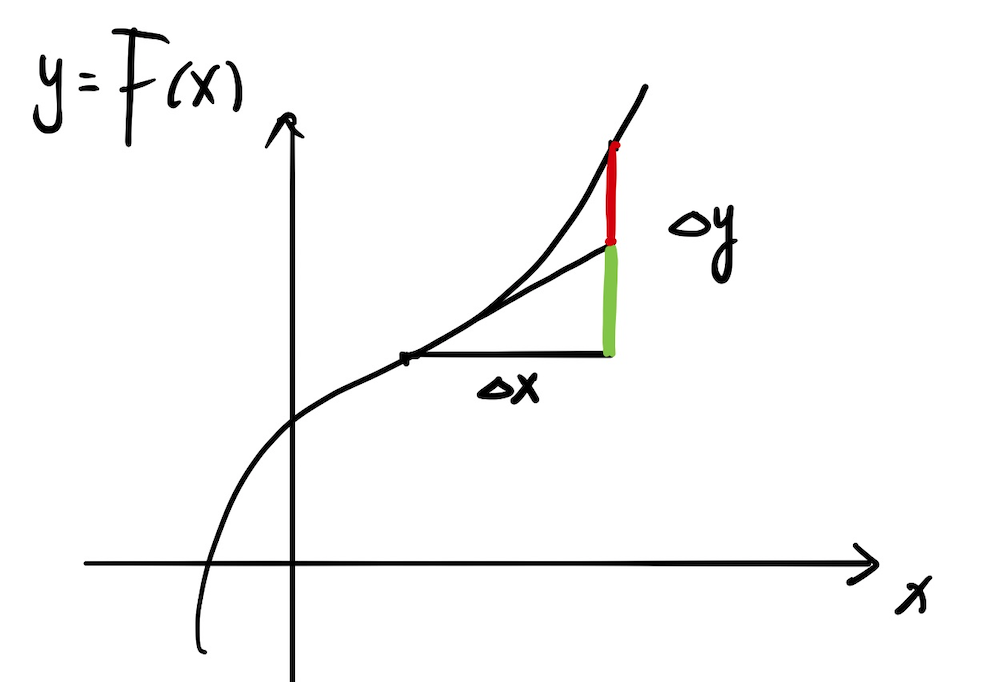
这里理解和曲边梯形的例子一样:F的增量,可以表示为无数个小增量$$f(x)dx$$的和
同样,也有一个问题:凭什么$f(x)dx$可以代替F实际的增量
将实际的增量
显然对于红色部分e有: $$ e = \Delta y - f(x) \Delta x $$ 那么在整个积分区间内,所有红色部分的和为:(注意下面这个式子为了方便理解作了一些简化) $$ \sum e = (\Delta y - f(x) \Delta x)\frac{a-b}{\Delta x} $$ 积分公式成立的等价条件是,当$\Delta x$趋向于零时,红色部分的面积之和取向于零,即: $$ {align} \lim_{\Delta x \to 0}{ (\Delta y - f(x) \Delta x)\frac{a-b}{\Delta x}} = 0 \ \lim_{\Delta x \to 0}{\frac{\Delta y}{\Delta x}}= f(x) $$ {end} 可以看到成立的条件就是微分的定义
从狭义上来理解,微积分就是积分和微分,积分是无穷求和,而微分可以看作无穷求和的工具
广泛一点理解,微积分是一套处理“无穷”之间关系的工具,理解”无穷“也就理解了微积分
”无穷“是一个数学上的抽象概念,源于观察世界的尺度问题,而且是在高尺度观察低尺度产生的问题
在实际中,应用微积分的地方都是一些比较宏观的地方
比如计算一个杯子的质量,已知杯子的密度分布和杯子的形状,我们需要做的就是:密度乘以体积微元,然后再积分。但是这里隐含一个假设就是,密度是可微的,体积是无限可分的。这在宏观世界中好像并不是大问题。但是在分子原子的这个尺度下,还能用密度乘以体积的方法计算杯子的质量么?
回到最开始的公交车的例子,我们的假设是,时间是可以无限细分的,即时刻是存在的。但是时刻在微观尺度下真的存在么?
所以数学总是和哲学,或者说和神学有着密切的联系。是笑谈,也有道理。世界是连续的么?无穷存在么?这样的问题总像是在跟结界的边缘试探。