Data Dimension reduction
PCA是一种无监督的数据降维方法,用数据中最主要的方面代替原始数据。
当小姐姐的备胎们都有183-186身高的时候,即使不考虑具体的人如何,也可以推断出身高特征对分类的结果影响不大,可以省略。
然而,大部分时候数据不是按照特征坐标系来降维的,而是在新的坐标系下。我们所说的特征是对人拥有具象意义的,但是并不一定是数据的特征。PCA的主要问题在于如何找到合适的投影方法确定合适的数据特征坐标系(找到主元principal component)。
由此二维的面积-房价数据就可以简化为一个一维主元
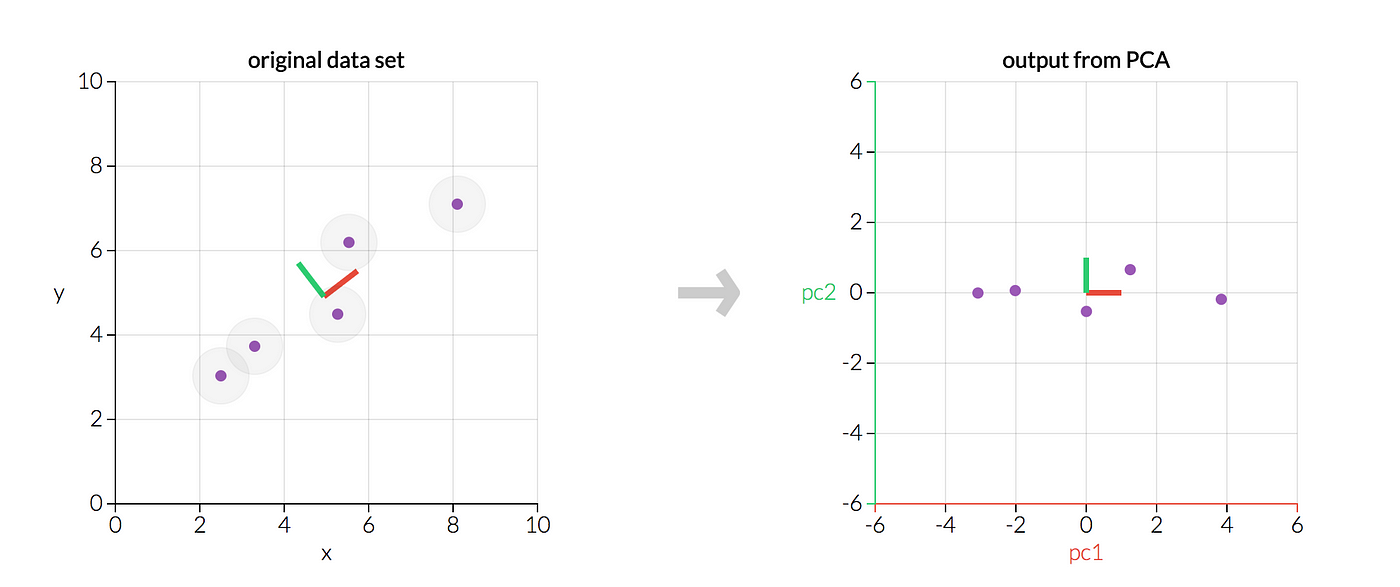
第一个新坐标轴选择是原始数据中方差最大的方向(即数据特征最突出的方向),第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴。我们只保留前k维,这就意味着数据特征明显的维度被保留下来,不明显的被忽略。由此,n维数据就被降维到k维。
- 对所有的样本进行中心化:$x^{(i)}=x^{(i)}-\frac{1}{m}\sum^m_{j=1}x^{(j)}$
- 计算样本的协方差矩阵
$XX^T$ -
- 对矩阵$XX^T$进行特征值分解,
- 对矩阵$XX^T$进行奇异值分解
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前 k 行组成矩阵 P;
-
$Y=PX$ 即为降维到 k 维后的数据。
方差只是对一维来说的,对于高维数据我们能需要使用协方差矩阵来表示特征的分散程度。
至此,我们得到了降维问题的优化目标:将一组 M 维向量降为 K 维,其目标是选择 K 个单位正交基,使得原始数据变换到这组基上后,各变量两两间协方差为 0,而变量方差则尽可能大(在正交的约束下,取最大的 K 个方差)。
我们如果可以把协方差矩阵对角化,然后将对角化后的矩阵按元素的大小排列,那么这个矩阵的前K行就是要寻找的新坐标系的基。用其前K行特征值对应的特征向量组成的矩阵P乘以原数据X即可得到降维后的K维数据Y。
- 特征值与特征向量
如果一个向量v是矩阵A的特征向量,将一定可以表示成下面的形式:
其中,λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。
- 特征值分解矩阵
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式:
其中,Q是矩阵A的特征向量组成的矩阵,$\Sigma$则是一个对角阵,对角线上的元素就是特征值。
奇异值分解是一个能适用于任意矩阵的一种分解的方法,对于任意矩阵A总是存在一个奇异值分解:
假设A是一个$mn$的矩阵,那么得到的U是一个$mm$的方阵,U里面的正交向量被称为左奇异向量。Σ是一个$mn$的矩阵,Σ除了对角线其它元素都为0,对角线上的元素称为奇异值。 $V^T$ 是 $V$ 的转置矩阵,是一个$nn$的矩阵,它里面的正交向量被称为右奇异值向量。而且一般来讲,我们会将Σ上的值按从大到小的顺序排列。
SVD分解矩阵A的步骤:
(1) 求
(2) 求
(3) 将
(4)
优势: 奇异矩阵V将数据用于对行数的压缩。右奇异矩阵U可以用于对列(即特征维度)的压缩。 $$X'{m\times k}=X{m\times n}V_{n\times k}^T$$