diff --git a/docs/AI/CS231n/CS231n_notes.md b/docs/AI/CS231n/CS231n_notes.md
new file mode 100644
index 00000000..e773b78a
--- /dev/null
+++ b/docs/AI/CS231n/CS231n_notes.md
@@ -0,0 +1,1952 @@
+# Computer Vision
+
+This note is based on [GitHub - DaizeDong/Stanford-CS231n-2021-and-2022: Notes and slides for Stanford CS231n 2021 & 2022 in English. I merged the contents together to get a better version. Assignments are not included. 斯坦福cs231n的课程笔记(英文版本,不含实验代码),将2021与2022两年的课程进行了合并,分享以供交流。](https://github.com/DaizeDong/Stanford-CS231n-2021-and-2022/)
+And I will add some blogs, articles and other understanding.
+
+| Topic | Chapter |
+| ---------------------------------------------------- | ------- |
+| Deep Learning Basics | 2 - 4 |
+| Perceiving and Understanding the Visual World | 5 - 12 |
+| Reconstructing and Interacting with the Visual World | 13 - 16 |
+| Human-Centered Applications and Implications | 17 - 18 |
+
+## 1 - Introduction
+
+A brief history of computer vision & deep learning...
+
+## 2 - Image Classification
+
+**Image Classification:** A core task in Computer Vision. The main drive to the progress of CV.
+
+**Challenges:** Viewpoint variation, background clutter, illumination, occlusion, deformation, intra-class variation...
+
+### K Nearest Neighbor
+
+**Hyperparameters:** Distance metric ($p$ norm), $k$ number.
+
+Choose hyperparameters using validation set.
+
+Never use k-Nearest Neighbor with pixel distance.
+
+
+
+### Linear Classifier
+
+Pass...
+
+## 3 - Loss Functions and Optimization
+
+### Loss Functions
+
+| Dataset | $\big\{(x_i,y_i)\big\}_{i=1}^N\\$ |
+| --------------------------------- | ------------------------------------------------------------ |
+| Loss Function | $L=\frac{1}{N}\sum_{i=1}^NL_i\big(f(x_i,W),y_i\big)\\$ |
+| Loss Function with Regularization | $L=\frac{1}{N}\sum_{i=1}^NL_i\big(f(x_i,W),y_i\big)+\lambda R(W)\\$ |
+
+**Motivation:** Want to interpret raw classifier scores as probabilities.
+
+| Softmax Classifier | $p_i=Softmax(y_i)=\frac{\exp(y_i)}{\sum_{j=1}^N\exp(y_j)}\\$ |
+| -------------------------------------- | ------------------------------------------------------------ |
+| Cross Entropy Loss | $L_i=-y_i\log p_i\\$ |
+| Cross Entropy Loss with Regularization | $L=-\frac{1}{N}\sum_{i=1}^Ny_i\log p_i+\lambda R(W)\\$ |
+
+
+
+### Optimization
+
+#### SGD with Momentum
+
+**Problems that SGD can't handle:**
+
+1. Inequality of gradient in different directions.
+2. Local minima and saddle point (much more common in high dimension).
+3. Noise of gradient from mini-batch.
+
+**Momentum:** Build up “velocity” $v_t$ as a running mean of gradients.
+
+| SGD | SGD + Momentum |
+| --------------------------------- | ------------------------------------------------------------ |
+| $x_{t+1}=x_t-\alpha\nabla f(x_t)$ | $\begin{align}&v_{t+1}=\rho v_t+\nabla f(x_t)\\&x_{t+1}=x_t-\alpha v_{t+1}\end{align}$ |
+| Naive gradient descent. | $\rho$ gives "friction", typically $\rho=0.9,0.99,0.999,...$ |
+
+**Nesterov Momentum:** Use the derivative on point $x_t+\rho v_t$ as gradient instead point $x_t$.
+
+| Momentum | Nesterov Momentum |
+| ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $\begin{align}&v_{t+1}=\rho v_t+\nabla f(x_t)\\&x_{t+1}=x_t-\alpha v_{t+1}\end{align}$ | $\begin{align}&v_{t+1}=\rho v_t+\nabla f(x_t+\rho v_t)\\&x_{t+1}=x_t-\alpha v_{t+1}\end{align}$ |
+| Use gradient at current point. | Look ahead for the gradient in velocity direction. |
+
+
+
+#### AdaGrad and RMSProp
+
+**AdaGrad:** Accumulate squared gradient, and gradually decrease the step size.
+
+**RMSProp:** Accumulate squared gradient while decaying former ones, and gradually decrease the step size. ("Leaky AdaGrad")
+
+| AdaGrad | RMSProp |
+| ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $\begin{align}\text{Initialize:}&\\&r:=0\\\text{Update:}&\\&r:=r+\Big[\nabla f(x_t)\Big]^2\\&x_{t+1}=x_t-\alpha\frac{\nabla f(x_t)}{\sqrt{r}}\end{align}$ | $\begin{align}\text{Initialize:}&\\&r:=0\\\text{Update:}&\\&r:=\rho r+(1-\rho)\Big[\nabla f(x_t)\Big]^2\\&x_{t+1}=x_t-\alpha\frac{\nabla f(x_t)}{\sqrt{r}}\end{align}$ |
+| Continually accumulate squared gradients. | $\rho$ gives "decay rate", typically $\rho=0.9,0.99,0.999,...$ |
+
+#### Adam
+
+Sort of like "RMSProp + Momentum".
+
+| Adam (simple version) | Adam (full version) |
+| ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $\begin{align}\text{Initialize:}&\\&r_1:=0\\&r_2:=0\\\text{Update:}&\\&r_1:=\beta_1r_1+(1-\beta_1)\nabla f(x_t)\\&r_2:=\beta_2r_2+(1-\beta_2)\Big[\nabla f(x_t)\Big]^2\\&x_{t+1}=x_t-\alpha\frac{r_1}{\sqrt{r_2}}\end{align}$ | $\begin{align}\text{Initialize:}\\&r_1:=0\\&r_2:=0\\\text{For }i\text{:}\\&r_1:=\beta_1r_1+(1-\beta_1)\nabla f(x_t)\\&r_2:=\beta_2r_2+(1-\beta_2)\Big[\nabla f(x_t)\Big]^2\\&r_1'=\frac{r_1}{1-\beta_1^i}\\&r_2'=\frac{r_2}{1-\beta_2^i}\\&x_{t+1}=x_t-\alpha\frac{r_1'}{\sqrt{r_2'}}\end{align}$ |
+| Build up “velocity” for both gradient and squared gradient. | Correct the "bias" that $r_1=r_2=0$ for the first few iterations. |
+
+#### Overview
+
+|  |  |
+| :----------------------------------------------------------: | :----------------------------------------------------------: |
+
+#### Learning Rate Decay
+
+Reduce learning rate at a few fixed points to get a better convergence over time.
+
+$\alpha_0$ : Initial learning rate.
+
+$\alpha_t$ : Learning rate in epoch $t$.
+
+$T$ : Total number of epochs.
+
+| Method | Equation | Picture |
+| ------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
+| Step | Reduce $\alpha_t$ constantly in a fixed step. | 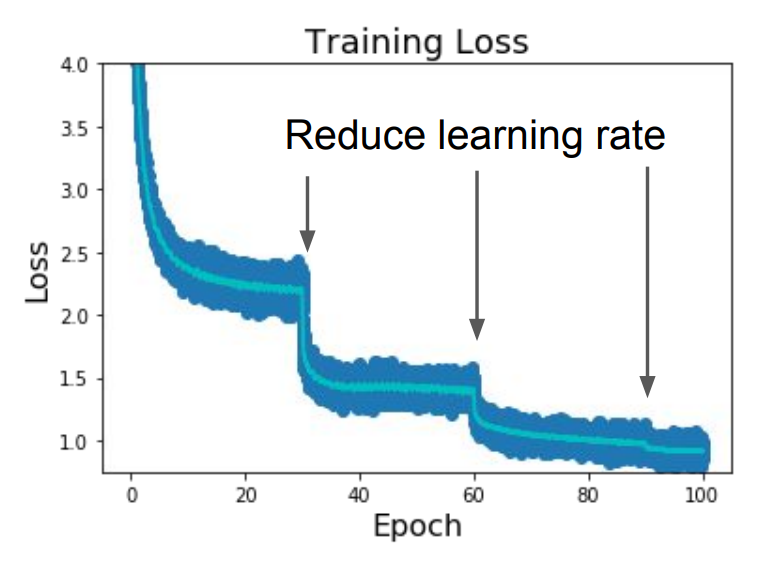 |
+| Cosine | $\begin{align}\alpha_t=\frac{1}{2}\alpha_0\Bigg[1+\cos(\frac{t\pi}{T})\Bigg]\end{align}$ |  |
+| Linear | $\begin{align}\alpha_t=\alpha_0\Big(1-\frac{t}{T}\Big)\end{align}$ |  |
+| Inverse Sqrt | $\begin{align}\alpha_t=\frac{\alpha_0}{\sqrt{t}}\end{align}$ |  |
+
+High initial learning rates can make loss explode, linearly increasing learning rate in the first few iterations can prevent this.
+
+**Learning rate warm up:**
+
+
+
+**Empirical rule of thumb:** If you increase the batch size by $N$, also scale the initial learning rate by $N$ .
+
+#### Second-Order Optimization
+
+| | Picture | Time Complexity | Space Complexity |
+| ------------ | ------------------------------------------------------- | ----------------------------------- | ----------------------------------- |
+| First Order |  | $O(n)$ | $O(n)$ |
+| Second Order |  | $O(n^2)$ with **BGFS** optimization | $O(n)$ with **L-BGFS** optimization |
+
+**L-BGFS :** Limited memory BGFS.
+
+1. Works very well in full batch, deterministic $f(x)$.
+2. Does not transfer very well to mini-batch setting.
+
+#### Summary
+
+| Method | Performance |
+| -------------- | ------------------------------------------------------------ |
+| Adam | Often chosen as default method.
Work ok even with constant learning rate. |
+| SGD + Momentum | Can outperform Adam.
Require more tuning of learning rate and schedule. |
+| L-BGFS | If can afford to do full batch updates then try out. |
+
+- An article about gradient descent: [Anoverview of gradient descent optimization algorithms](https://arxiv.org/pdf/1609.04747)
+- A blog: [An updated overview of recent gradient descent algorithms – John Chen – ML at Rice University](https://johnchenresearch.github.io/demon/)
+
+## 4 - Neural Networks and Backpropagation
+
+### Neural Networks
+
+**Motivation:** Inducted bias can appear to be high when using human-designed features.
+
+**Activation:** Sigmoid, tanh, ReLU, LeakyReLU...
+
+**Architecture:** Input layer, hidden layer, output layer.
+
+**Do not use the size of a neural network as the regularizer. Use regularization instead!**
+
+**Gradient Calculation:** Computational Graph + Backpropagation.
+
+### Backpropagation
+
+Using Jacobian matrix to calculate the gradient of each node in a computation graph.
+
+Suppose that we have a computation flow like this:
+
+
+
+| Input X | Input W | Output Y |
+| ----------------------------------------------------- | ------------------------------------------------------------ | ----------------------------------------------------- |
+| $X=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}$ | $W=\begin{bmatrix}w_{11}&w_{12}&\cdots&w_{1n}\\w_{21}&w_{22}&\cdots&w_{2n}\\\vdots&\vdots&\ddots&\vdots\\w_{m1}&w_{m2}&\cdots&w_{mn}\end{bmatrix}$ | $Y=\begin{bmatrix}y_1\\y_2\\\vdots\\y_m\end{bmatrix}$ |
+| $n\times 1$ | $m\times n$ | $m\times 1$ |
+
+After applying feed forward, we can calculate gradients like this:
+
+
+
+| Derivative Matrix of X | Jacobian Matrix of X | Derivative Matrix of Y |
+| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $D_X=\begin{bmatrix}\frac{\partial L}{\partial x_1}\\\frac{\partial L}{\partial x_2}\\\vdots\\\frac{\partial L}{\partial x_n}\end{bmatrix}$ | $J_X=\begin{bmatrix}\frac{\partial y_1}{\partial x_1}&\frac{\partial y_1}{\partial x_2}&\cdots&\frac{\partial y_1}{\partial x_n}\\\frac{\partial y_2}{\partial x_1}&\frac{\partial y_2}{\partial x_2}&\cdots&\frac{\partial y_2}{\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial y_m}{\partial x_1}&\frac{\partial y_m}{\partial x_2}&\cdots&\frac{\partial y_m}{\partial x_n}\end{bmatrix}$ | $D_Y=\begin{bmatrix}\frac{\partial L}{\partial y_1}\\\frac{\partial L}{\partial y_2}\\\vdots\\\frac{\partial L}{\partial y_m}\end{bmatrix}$ |
+| $n\times 1$ | $m\times n$ | $m\times 1$ |
+
+| Derivative Matrix of W | Jacobian Matrix of W | Derivative Matrix of Y |
+| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $W=\begin{bmatrix}\frac{\partial L}{\partial w_{11}}&\frac{\partial L}{\partial w_{12}}&\cdots&\frac{\partial L}{\partial w_{1n}}\\\frac{\partial L}{\partial w_{21}}&\frac{\partial L}{\partial w_{22}}&\cdots&\frac{\partial L}{\partial w_{2n}}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial L}{\partial w_{m1}}&\frac{\partial L}{\partial w_{m2}}&\cdots&\frac{\partial L}{\partial w_{mn}}\end{bmatrix}$ | $J_W^{(k)}=\begin{bmatrix}\frac{\partial y_k}{\partial w_{11}}&\frac{\partial y_k}{\partial w_{12}}&\cdots&\frac{\partial y_k}{\partial w_{1n}}\\\frac{\partial y_k}{\partial w_{21}}&\frac{\partial y_k}{\partial w_{22}}&\cdots&\frac{\partial y_k}{\partial w_{2n}}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial y_k}{\partial w_{m1}}&\frac{\partial y_k}{\partial w_{m2}}&\cdots&\frac{\partial y_k}{\partial w_{mn}}\end{bmatrix}$
$J_W=\begin{bmatrix}J_W^{(1)}&J_W^{(2)}&\cdots&J_W^{(m)}\end{bmatrix}$ | $D_Y=\begin{bmatrix}\frac{\partial L}{\partial y_1}\\\frac{\partial L}{\partial y_2}\\\vdots\\\frac{\partial L}{\partial y_m}\end{bmatrix}$ |
+| $m\times n$ | $m\times m\times n$ | $ m\times 1$ |
+
+For each element in $D_X$ , we have:
+
+$D_{Xi}=\frac{\partial L}{\partial x_i}=\sum_{j=1}^m\frac{\partial L}{\partial y_j}\frac{\partial y_j}{\partial x_i}\\$
+
+## 5 - Convolutional Neural Networks
+
+### Convolution Layer
+
+#### Introduction
+
+**Convolve a filter with an image:** Slide the filter spatially within the image, computing dot products in each region.
+
+Giving a $32\times32\times3$ image and a $5\times5\times3$ filter, a convolution looks like:
+
+
+
+Convolve six $5\times5\times3$ filters to a $32\times32\times3$ image with step size $1$, we can get a $28\times28\times6$ feature:
+
+
+
+With an activation function after each convolution layer, we can build the ConvNet with a sequence of convolution layers:
+
+
+
+By **changing the step size** between each move for filters, or **adding zero-padding** around the image, we can modify the size of the output:
+
+
+
+#### $1\times1$ Convolution Layer
+
+This kind of layer makes perfect sense. It is usually used to change the dimension (channel) of features.
+
+A $1\times1$ convolution layer can also be treated as a full-connected linear layer.
+
+
+
+#### Summary
+
+| **Input** | |
+| ------------------------- | ---------------------------- |
+| image size | $W_1\times H_1\times C$ |
+| filter size | $F\times F\times C$ |
+| filter number | $K$ |
+| stride | $S$ |
+| zero padding | $P$ |
+| **Output** | |
+| output size | $W_2\times H_2\times K$ |
+| output width | $W_2=\frac{W_1-F+2P}{S}+1\\$ |
+| output height | $H_2=\frac{H_1-F+2P}{S}+1\\$ |
+| **Parameters** | |
+| parameter number (weight) | $F^2CK$ |
+| parameter number (bias) | $K$ |
+
+### Pooling layer
+
+Make the representations smaller and more manageable.
+
+**An example of max pooling:**
+
+
+
+| **Input** | |
+| -------------- | ------------------------- |
+| image size | $W_1\times H_1\times C$ |
+| spatial extent | $F\times F$ |
+| stride | $S$ |
+| **Output** | |
+| output size | $W_2\times H_2\times C$ |
+| output width | $W_2=\frac{W_1-F}{S}+1\\$ |
+| output height | $H_2=\frac{H_1-F}{S}+1\\$ |
+
+### Convolutional Neural Networks (CNN)
+
+CNN stack CONV, POOL, FC layers.
+
+**CNN Trends:**
+
+1. Smaller filters and deeper architectures.
+2. Getting rid of POOL/FC layers (just CONV).
+
+**Historically architectures of CNN looked like:**
+
+
+
+where usually $m$ is large, $0\le n\le5$, $0\le k\le2$.
+
+Recent advances such as **ResNet** / **GoogLeNet** have challenged this paradigm.
+
+## 6 - CNN Architectures
+
+Best model in ImageNet competition:
+
+
+
+### AlexNet
+
+8 layers.
+
+First use of ConvNet in image classification problem.
+
+Filter size decreases in deeper layer.
+
+Channel number increases in deeper layer.
+
+
+
+
+
+### VGG
+
+19 layers. (also provide 16 layers edition)
+
+Static filter size ($3\times3$) in all layers:
+
+1. The effective receptive field expands with the layer gets deeper.
+2. Deeper architecture gets more non-linearities and few parameters.
+
+
+
+Most memory is in early convolution layers.
+
+Most parameter is in late FC layers.
+
+
+
+
+
+### GoogLeNet
+
+22 layers.
+
+No FC layers, only 5M parameters. ( $8.3\%$ of AlexNet, $3.7\%$ of VGG )
+
+Devise efficient "inception module".
+
+#### Inception Module
+
+Design a good local network topology (network within a network) and then stack these modules on top of each other.
+
+**Naive Inception Module:**
+
+1. Apply parallel filter operations on the input from previous layer.
+2. Concatenate all filter outputs together channel-wise.
+3. **Problem:** The depth (channel number) increases too fast, costing expensive computation.
+
+
+
+**Inception Module with Dimension Reduction:**
+
+1. Add "bottle neck" layers to reduce the dimension.
+2. Also get fewer computation cost.
+
+
+
+#### Architecture
+
+
+
+
+
+### ResNet
+
+152 layers for ImageNet.
+
+Devise "residual connections".
+
+Use BN in place of dropout.
+
+#### Residual Connections
+
+**Hypothesis:** Deeper models have more representation power than shallow ones. But they are harder to optimize.
+
+**Solution:** Use network layers to fit a residual mapping instead of directly trying to fit a desired underlying mapping.
+
+
+
+It is necessary to use ReLU as activation function, in order to apply identity mapping when $F(x)=0$ .
+
+#### Architecture
+
+
+
+
+
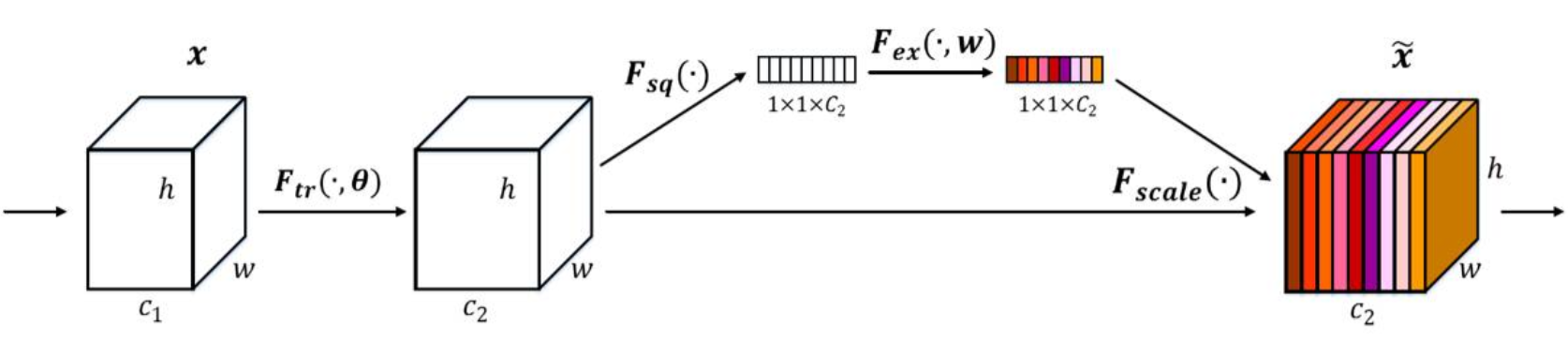
+### SENet
+
+Using ResNeXt-152 as a base architecture.
+
+Add a “feature recalibration” module. **(adjust weights of each channel)**
+
+Using the **global avg-pooling layer** + **FC layers** to determine feature map weights.
+
+
+
+
+
+### Improvements of ResNet
+
+Wide Residual Networks, ResNeXt, DenseNet, MobileNets...
+
+### Other Interesting Networks
+
+**NASNet:** Neural Architecture Search with Reinforcement Learning.
+
+**EfficientNet:** Smart Compound Scaling.
+
+## 7 - Training Neural Networks
+
+### Activation Functions
+
+| Activation | Usage |
+| ----------------------------- | ------------------------------------------------ |
+| Sigmoid, tanh | Do not use. |
+| ReLU | Use as default. |
+| Leaky ReLU, Maxout, ELU, SELU | Replace ReLU to squeeze out some marginal gains. |
+| Swish | No clear usage. |
+
+### Data Processing
+
+Apply centralization and normalization before training.
+
+In practice for pictures, usually we apply channel-wise centralization only.
+
+### Weight Initialization
+
+Assume that we have 6 layers in a network.
+
+$D_i$ : input size of layer $i$
+
+$W_i$ : weights in layer $i$
+
+$X_i$ : output after activation of layer $i$, we have $X_i=g(Z_i)=g(W_iX_{i-1}+B_i)$
+
+**We initialize each parameter in $W_i$ randomly in $[-k_i,k_i]$ .**
+
+| Tanh Activation | Output Distribution |
+| :----------------------------------------------------: | :------------------------------------------------------: |
+| $k_i=0.01$ |  |
+| $k_i=0.05$ |  |
+| **Xavier Initialization** $k_i=\frac{1}{\sqrt{D_i}\\}$ |  |
+
+When $k_i=0.01$, the variance keeps decreasing as the layer gets deeper. As a result, the output of each neuron in deep layer will all be 0. The partial derivative $\frac{\partial Z_i}{\partial W_i}=X_{i-1}=0\\$. (no gradient)
+
+When $k_i=0.05$, most neurons is saturated. The partial derivative $\frac{\partial X_i}{\partial Z_i}=g'(Z_i)=0\\$. (no gradient)
+
+**To solve this problem, We need to keep the variance same in each layer.**
+
+Assuming that $Var\big(X_{i-1}^{(1)}\big)=Var\big(X_{i-1}^{(2)}\big)=\dots=Var\big(X_{i-1}^{(D_i)}\big)$
+
+We have $Z_i=X_{i-1}^{(1)}W_i^{(:,1)}+X_{i-1}^{(2)}W_i^{(:,2)}+\dots+X_{i-1}^{(D_i)}W_i^{(:,D_i)}=\sum_{n=1}^{D_i}X_{i-1}^{(n)}W_i^{(:,n)}\\$
+
+We want $Var\big(Z_i\big)=Var\big(X_{i-1}^{(n)}\big)$
+
+**Let's do some conduction:**
+
+$\begin{aligned}Var\big(Z_i\big)&=Var\Bigg(\sum_{n=1}^{D_i}X_{i-1}^{(n)}W_i^{(:,n)}\Bigg)\\&=D_i\ Var\Big(X_{i-1}^{(n)}W_i^{(:,n)}\Big)\\&=D_i\ Var\Big(X_{i-1}^{(n)}\Big)\ Var\Big(W_i^{(:,n)}\Big)\end{aligned}$
+
+So $Var\big(Z_i\big)=Var\big(X_{i-1}^{(n)}\big)$ only when $Var\Big(W_i^{(:,n)}\Big)=\frac{1}{D_i}\\$, that is to say $k_i=\frac{1}{\sqrt{D_i}}\\$
+
+| ReLU Activation | Output Distribution |
+| :----------------------------------------------------: | :----------------------------------------------------: |
+| **Xavier Initialization** $k_i=\frac{1}{\sqrt{D_i}\\}$ |  |
+| **Kaiming Initialization** $k_i=\sqrt{2D_i}$ |  |
+
+For ReLU activation, when using xavier initialization, there still exist "variance decreasing" problem.
+
+We can use kaiming initialization instead to fix this.
+
+### Batch Normalization
+
+Force the inputs to be "nicely scaled" at each layer.
+
+$N$ : batch size
+
+$D$ : feature size
+
+$x$ : input with shape $N\times D$
+
+$\gamma$ : learnable scale and shift parameter with shape $D$
+
+$\beta$ : learnable scale and shift parameter with shape $D$
+
+**The procedure of batch normalization:**
+
+1. Calculate channel-wise mean $\mu_j=\frac{1}{N}\sum_{i=1}^Nx_{i,j}\\$ . The result $\mu$ with shape $D$ .
+2. Calculate channel-wise variance $\sigma_j^2=\frac{1}{N}\sum_{i=1}^N(x_{i,j}-\mu_j)^2\\$ . The result $\sigma^2$ with shape $D$ .
+3. Calculate normalized $\hat{x}_{i,j}=\frac{x_{i,j}-\mu_j}{\sqrt{\sigma_j^2+\epsilon}}\\$ . The result $\hat{x}$ with shape $N\times D$ .
+4. Scale normalized input to get output $y_{i,j}=\gamma_j\hat{x}_{i,j}+\beta_j$ . The result $y$ with shape $N\times D$ .
+
+ **Why scale:** The constraint "zero-mean, unit variance" may be too hard.
+
+
+
+**Pros:**
+
+1. Makes deep networks much easier to train!
+2. Improves gradient flow.
+3. Allows higher learning rates, faster convergence.
+4. Networks become more robust to initialization.
+5. Acts as regularization during training.
+6. Zero overhead at test-time: can be fused with conv!
+
+**Cons:**
+
+ Behaves differently during training and testing: this is a very common source of bugs!
+
+
+
+### Transfer Learning
+
+Train on a pre-trained model with other datasets.
+
+**An empirical suggestion:**
+
+| | **very similar dataset** | **very different dataset** |
+| ----------------------- | ----------------------------------- | ------------------------------------------------------------ |
+| **very little data** | Use Linear Classifier on top layer. | You’re in trouble… Try linear classifier from different stages. |
+| **quite a lot of data** | Finetune a few layers. | Finetune a larger number of layers. |
+
+### Regularization
+
+#### Common Pattern of Regularization
+
+Training: Add some kind of randomness. $y=f(x,z)$
+
+Testing: Average out randomness (sometimes approximate). $y=f(x)=E_z\big[f(x,z)\big]=\int p(z)f(x,z)dz\\$
+
+#### Regularization Term
+
+L2 regularization: $R(W)=\sum_k\sum_lW_{k,l}^2$ (weight decay)
+
+L1 regularization: $R(W)=\sum_k\sum_l|W_{k,l}|$
+
+Elastic net : $R(W)=\sum_k\sum_l\big(\beta W_{k,l}^2+|W_{k,l}|\big)$ (L1+L2)
+
+#### Dropout
+
+Training: Randomly set some neurons to 0 with a probability $p$ .
+
+Testing: Each neuron multiplies by dropout probability $p$ . (scale the output back)
+
+**More common:** Scale the output with $\frac{1}{p}$ when training, keep the original output when testing.
+
+
+
+**Why dropout works:**
+
+1. Forces the network to have a redundant representation. Prevents co-adaptation of features.
+2. **Another interpretation:** Dropout is training a large ensemble of models (that share parameters).
+
+
+
+#### Batch Normalization
+
+See above.
+
+#### Data Augmentation
+
+1. Horizontal Flips
+2. Random Crops and Scales
+3. Color Jitter
+4. Rotation
+5. Stretching
+6. Shearing
+7. Lens Distortions
+8. ...
+
+There also exists automatic data augmentation method using neural networks.
+
+#### Other Methods and Summary
+
+**DropConnect**: Drop connections between neurons.
+
+**Fractional Max Pooling:** Use randomized pooling regions.
+
+**Stochastic Depth**: Skip some layers in the network.
+
+**Cutout:** Set random image regions to zero.
+
+**Mixup:** Train on random blends of images.
+
+| Regularization Method | Usage |
+| --------------------------------------- | ---------------------------------- |
+| Dropout | For large fully-connected layers. |
+| Batch Normalization & Data Augmentation | Almost always a good idea. |
+| Cutout & Mixup | For small classification datasets. |
+
+### Hyperparameter Tuning
+
+| Most Common Hyperparameters | Less Sensitive Hyperparameters |
+| ------------------------------------------------------------ | ------------------------------ |
+| learning rate
learning rate decay schedule
weight decay | setting of momentum
... |
+
+**Tips on hyperparameter tuning:**
+
+1. Prefer one validation fold to cross-validation.
+2. Search for hyperparameters on log scale. (e.g. multiply the hyperparameter by a fixed number $k$ at each search)
+3. Prefer **random search** to grid search.
+4. Careful with best values on border.
+5. Stage your search from coarse to fine.
+
+
+
+#### Implementation
+
+Have a **worker** that continuously samples random hyperparameters and performs the optimization. During the training, the worker will keep track of the validation performance after every epoch, and writes a model checkpoint to a file.
+
+Have a **master** that launches or kills workers across a computing cluster, and may additionally inspect the checkpoints written by workers and plot their training statistics.
+
+#### Common Procedures
+
+1. **Check initial loss.**
+
+ Turn off weight decay, sanity check loss at initialization $\log(C)$ for softmax with $C$ classes.
+
+2. **Overfit a small sample. (important)**
+
+ Try to train to 100% training accuracy on a small sample of training data.
+
+ Fiddle with architecture, learning rate, weight initialization.
+
+3. **Find learning rate that makes loss go down.**
+
+ Use the architecture from the previous step, use all training data, turn on small weight decay, find a learning rate that makes the loss drop significantly within 100 iterations.
+
+ Good learning rates to try: $0.1,0.01,0.001,0.0001,\dots$
+
+4. **Coarse grid, train for 1-5 epochs.**
+
+ Choose a few values of learning rate and weight decay around what worked from Step 3, train a few models for 1-5 epochs.\
+
+ Good weight decay to try: $0.0001,0.00001,0$
+
+5. **Refine grid, train longer.**
+
+ Pick best models from Step 4, train them for longer (10-20 epochs) without learning rate decay.
+
+6. **Look at loss and accuracy curves.**
+7. **GOTO step 5.**
+
+### Gradient Checks
+
+[CS231n Convolutional Neural Networks for Visual Recognition](https://cs231n.github.io/neural-networks-3/#gradcheck)
+
+Compute analytical gradient manually using $f_a'=\frac{\partial f(x)}{\partial x}=\frac{f(x-h)-f(x+h)}{2h}\\$
+
+Get relative error between numerical gradient $f_n'$ and analytical gradient $f_a'$ using $E=\frac{|f_n'-f_a'|}{\max{|f_n'|,|f_a'|}}\\$
+
+| Relative Error | Result |
+| ------------------- | ------------------------------------------------------------ |
+| $E>10^{-2}$ | Probably $f_n'$ is wrong. |
+| $10^{-2}>E>10^{-4}$ | Not good, should check the gradient. |
+| $10^{-4}>E>10^{-6}$ | Okay for objectives with kinks. (e.g. ReLU)
Not good for objectives with no kink. (e.g. softmax, tanh) |
+| $10^{-7}>E$ | Good. |
+
+**Tips on gradient checks:**
+
+1. Use double precision.
+2. Use only few data points.
+3. Careful about kinks in the objective. (e.g. $x=0$ for ReLU activation)
+4. Careful with the step size $h$.
+5. Use gradient check after the loss starts to go down.
+6. Remember to turn off anything that may affect the gradient. (e.g. **regularization / dropout / augmentations**)
+7. Check only few dimensions for **every parameter**. (reduce time cost)
+
+## 8 - Visualizing and Understanding
+
+### Feature Visualization and Inversion
+
+#### Visualizing what models have learned
+
+| Visualize Areas | |
+| -------------------- | ------------------------------------------------------------ |
+| Filters | Visualize the raw weights of each convolution kernel. (better in the first layer) |
+| Final Layer Features | Run dimensionality reduction for features in the last FC layer. (PCA, t-SNE...) |
+| Activations | Visualize activated areas. ([Understanding Neural Networks Through Deep Visualization](https://arxiv.org/abs/1506.06579)) |
+
+#### Understanding input pixels
+
+##### Maximally Activating Patches
+
+1. Pick a layer and a channel.
+2. Run many images through the network, record values of the chosen channel.
+3. Visualize image patches that correspond to maximal activation features.
+
+For example, we have a layer with shape $128\times13\times13$. We pick the 17th channel from all 128 channels. Then we run many pictures through the network. During each run we can find a maximal activation feature among all the $13\times13$ features in channel 17. We then record the corresponding picture patch for each maximal activation feature. At last, we visualize all picture patches for each feature.
+
+This will help us find the relationship between each maximal activation feature and its corresponding picture patches.
+
+(each row of the following picture represents a feature)
+
+
+
+##### Saliency via Occlusion
+
+Mask part of the image before feeding to CNN, check how much predicted probabilities change.
+
+
+
+##### Saliency via Backprop
+
+1. Compute gradient of (unnormalized) class score with respect to image pixels.
+2. Take absolute value and max over RGB channels to get **saliency maps**.
+
+
+
+
+
+##### Intermediate Features via Guided Backprop
+
+1. Pick a single intermediate neuron. (e.g. one feature in a $128\times13\times13$ feature map)
+2. Compute gradient of neuron value with respect to image pixels.
+
+[Striving for Simplicity: The All Convolutional Net](https://arxiv.org/abs/1412.6806)
+
+Just like "Maximally Activating Patches", this could find the part of an image that a neuron responds to.
+
+
+
+
+
+##### Gradient Ascent
+
+Generate a synthetic image that maximally activates a neuron.
+
+1. Initialize image $I$ to zeros.
+2. Forward image to compute current scores $S_c(I)$ (for class $c$ before softmax).
+3. Backprop to get gradient of neuron value with respect to image pixels.
+4. Make a small update to the image.
+
+Objective: $\max S_c(I)-\lambda\lVert I\lVert^2$
+
+[Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps](https://arxiv.org/abs/1312.6034)
+
+
+
+
+
+### Adversarial Examples
+
+Find an fooling image that can make the network misclassify correctly-classified images when it is added to the image.
+
+1. Start from an arbitrary image.
+2. Pick an arbitrary class.
+3. Modify the image to maximize the class.
+4. Repeat until network is fooled.
+
+
+
+### DeepDream and Style Transfer
+
+#### Feature Inversion
+
+Given a CNN feature vector $\Phi_0$ for an image, find a new image $x$ that:
+
+1. Features of new image $\Phi(x)$ matches the given feature vector $\Phi_0$.
+2. "looks natural”. (image prior regularization)
+
+Objective: $\min \lVert\Phi(x)-\Phi_0\lVert+\lambda R(x)$
+
+[Understanding Deep Image Representations by Inverting Them](https://arxiv.org/abs/1412.0035)
+
+
+
+#### DeepDream: Amplify Existing Features
+
+Given an image, amplify the neuron activations at a layer to generate a new one.
+
+1. Forward: compute activations at chosen layer.
+2. Set gradient of chosen layer equal to its activation.
+3. Backward: Compute gradient on image.
+4. Update image.
+
+
+
+#### Texture Synthesis
+
+##### Nearest Neighbor
+
+1. Generate pixels one at a time in scanline order
+2. Form neighborhood of already generated pixels, copy the nearest neighbor from input.
+
+
+
+##### Neural Texture Synthesis
+
+Gram Matrix: [格拉姆矩阵(Gram matrix)详细解读](https://zhuanlan.zhihu.com/p/187345192)
+
+1. Pretrain a CNN on ImageNet.
+2. Run input texture forward through CNN, record activations on every layer.
+
+ Layer $i$ gives feature map of shape $C_i\times H_i\times W_i$.
+
+3. At each layer compute the **Gram matrix** $G_i$ giving outer product of features.
+
+ - Reshape feature map at layer $i$ to $C_i\times H_iW_i$.
+ - Compute the **Gram matrix** $G_i$ with shape $C_i\times C_i$.
+
+4. Initialize generated image from random noise.
+5. Pass generated image through CNN, compute **Gram matrix** $\hat{G}_l$ on each layer.
+6. Compute loss: Weighted sum of L2 distance between **Gram matrices**.
+
+ - $E_l=\frac{1}{aN_l^2M_l^2}\sum_{i,j}\Big(G_i^{(i,j)}-\hat{G}_i^{(i,j)}\Big)^2\\$
+ - $\mathcal{L}(\vec{x},\hat{\vec{x}})=\sum_{l=0}^L\omega_lE_l\\$
+
+7. Backprop to get gradient on image.
+8. Make gradient step on image.
+9. GOTO 5.
+
+[Texture Synthesis Using Convolutional Neural Networks](https://arxiv.org/abs/1505.07376)
+
+
+
+
+
+#### Style Transfer
+
+##### Feature + Gram Reconstruction
+
+
+
+
+
+**Problem:** Style transfer requires many forward / backward passes. Very slow!
+
+##### Fast Style Transfer
+
+
+
+
+
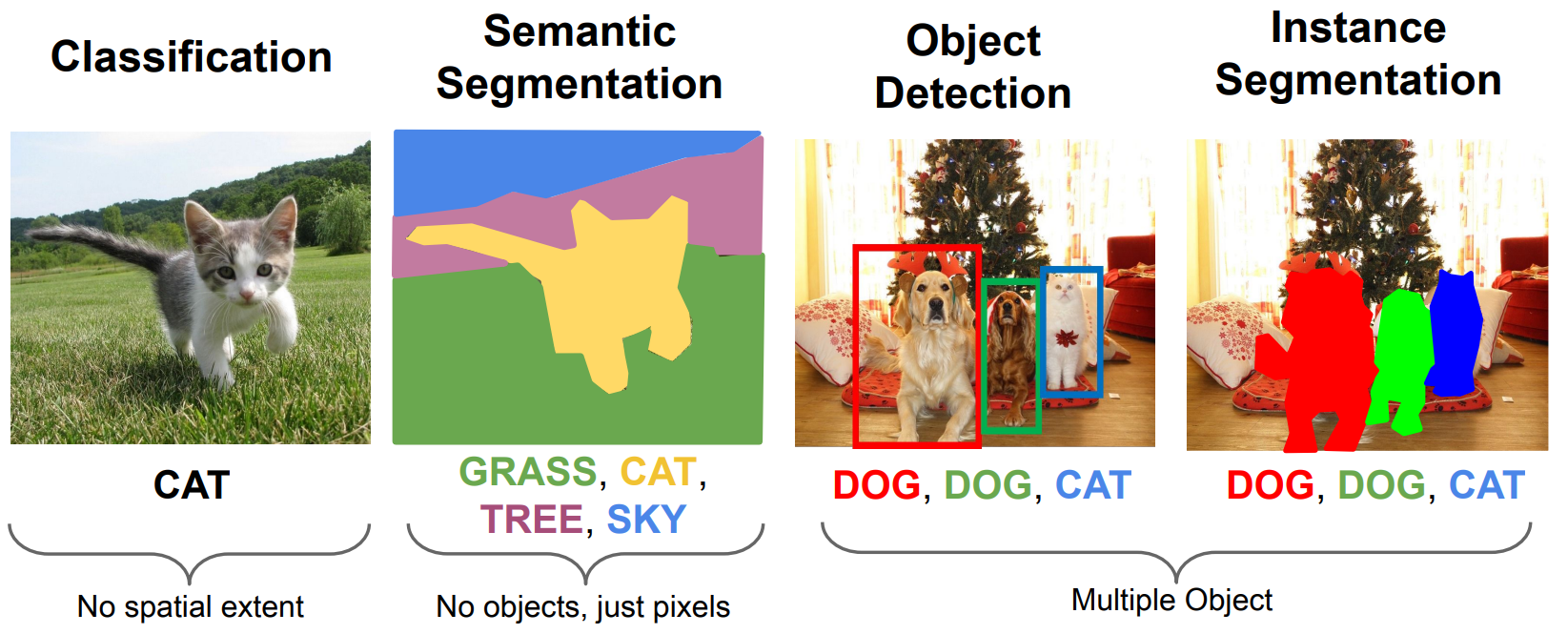
+## 9 - Object Detection and Image Segmentation
+
+
+
+### Semantic Segmentation
+
+**Paired Training Data:** For each training image, each pixel is labeled with a semantic category.
+
+
+
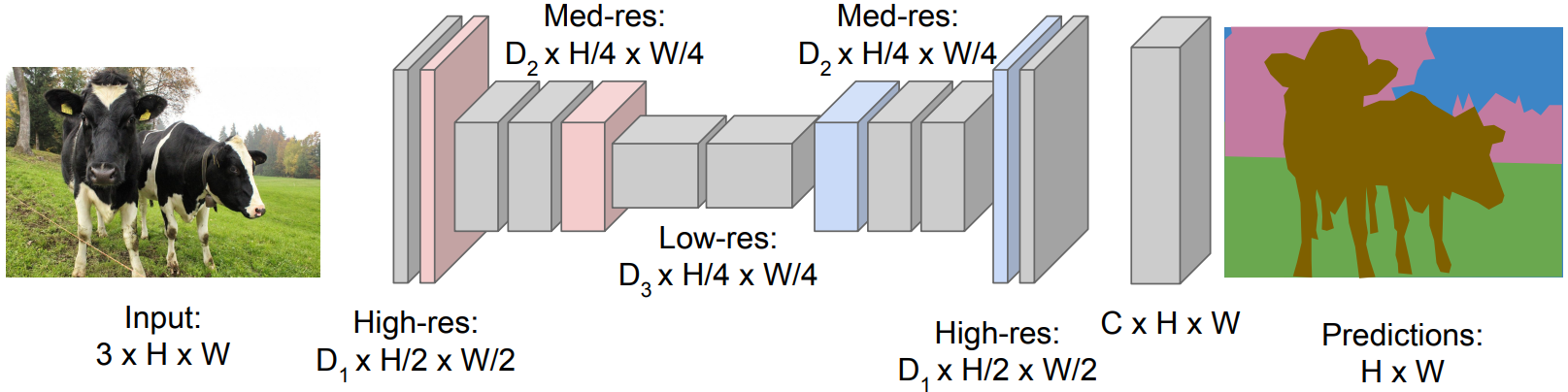
+**Fully Convolutional Network:** Design a network with only convolutional layers without downsampling operators to make predictions for pixels all at once!
+
+
+
+**Problem:** Convolutions at original image resolution will be very expensive...
+
+**Solution:** Design fully convolutional network with **downsampling** and **upsampling** inside it!
+
+- **Downsampling:** Pooling, strided convolution.
+- **Upsampling:** Unpooling, transposed convolution.
+
+**Unpooling:**
+
+| Nearest Neighbor | "Bed of Nails" | "Position Memory" |
+| :----------------------------------------------------: | :----------------------------------------------------------: | :--------------------------------------------------------: |
+|  |  |  |
+
+**Transposed Convolution:** (example size $3\times3$, stride $2$, pad $1$)
+
+| Normal Convolution | Transposed Convolution |
+| :----------------------------------------------------------: | :----------------------------------------------------------: |
+| 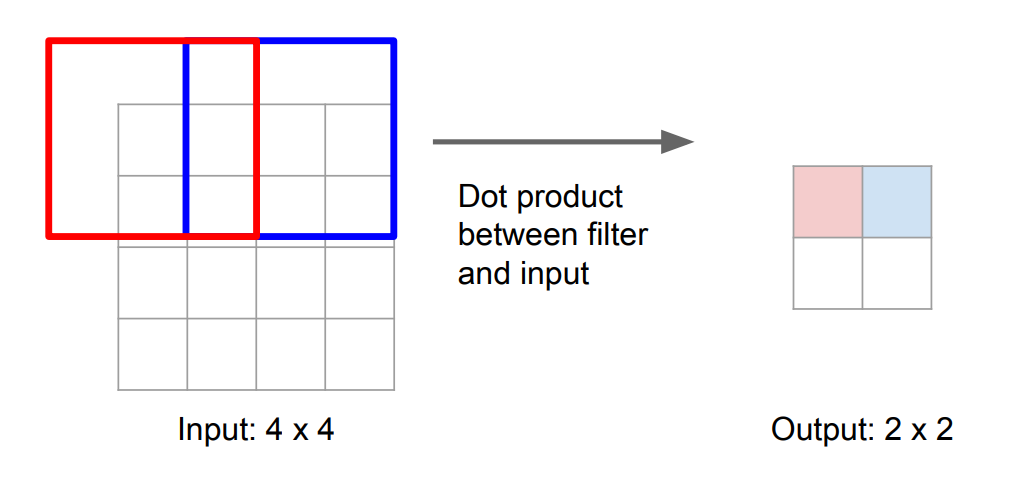 |  |
+|  | 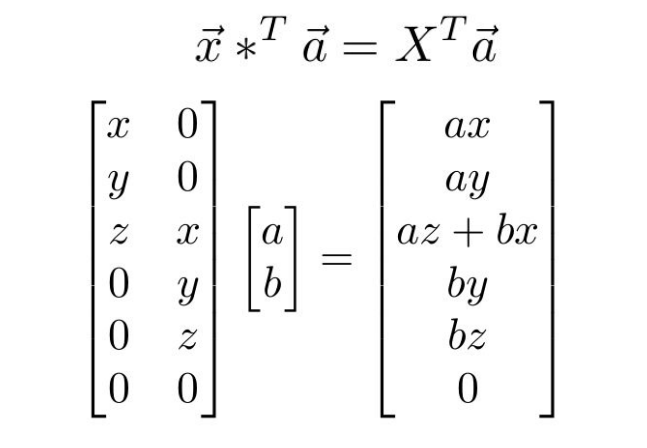 |
+
+
+
+### Object Detection
+
+#### Single Object
+
+Classification + Localization. (classification + regression problem)
+
+
+
+#### Multiple Object
+
+##### R-CNN
+
+Using selective search to find “blobby” image regions that are likely to contain objects.
+
+1. Find regions of interest (RoI) using selective search. (region proposal)
+2. Forward each region through ConvNet.
+3. Classify features with SVMs.
+
+**Problem:** Very slow. Need to do 2000 independent forward passes for each image!
+
+
+
+##### Fast R-CNN
+
+Pass the image through ConvNet before cropping. Crop the conv feature instead.
+
+1. Run whole image through ConvNet.
+2. Find regions of interest (RoI) from conv features using selective search. (**region proposal**)
+3. Classify RoIs using CNN.
+
+**Problem:** Runtime is dominated by region proposals. (about $90\%$ time cost)
+
+
+
+##### Faster R-CNN
+
+Insert Region Proposal Network (**RPN**) to predict proposals from features.
+
+Otherwise same as Fast R-CNN: Crop features for each proposal, classify each one.
+
+**Region Proposal Network (RPN) :** Slide many fixed windows over ConvNet features.
+
+1. Treat each point in the feature map as the **anchor**.
+
+ We have $k$ fixed windows (**anchor boxes**) of different size/scale centered with each anchor.
+
+2. For each anchor box, predict whether it contains an object.
+
+ For positive boxes, also predict a corrections to the ground-truth box.
+
+3. Slide anchor over the feature map, get the **“objectness” score** for each box at each point.
+4. Sort the “objectness” score, take top $300$ as the proposals.
+
+
+
+**Faster R-CNN is a Two-stage object detector:**
+
+1. First stage: Run once per image
+
+ Backbone network
+
+ Region proposal network
+
+2. Second stage: Run once per region
+
+ Crop features: RoI pool / align
+
+ Predict object class
+
+ Prediction bbox offset
+
+
+
+##### Single-Stage Object Detectors: YOLO
+
+[You Only Look Once: Unified, Real-Time Object Detection](https://arxiv.org/abs/1506.02640)
+
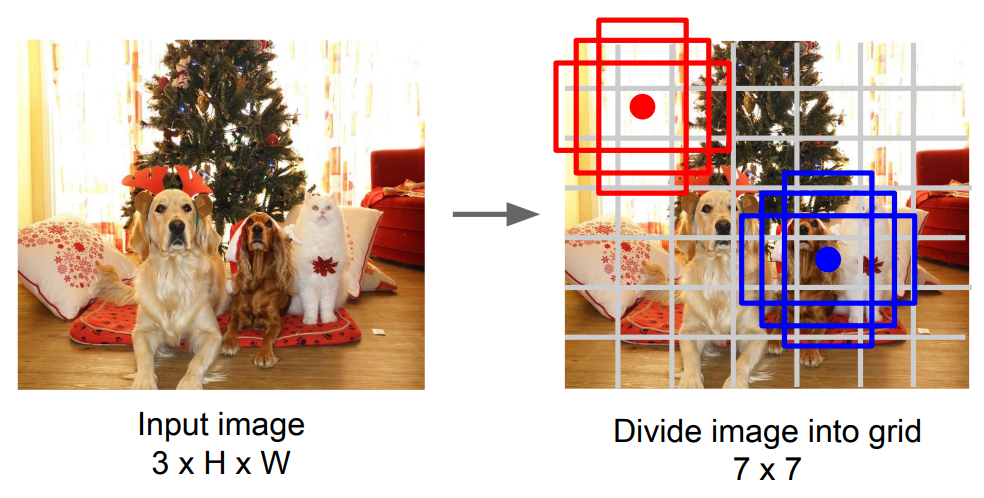
+1. Divide image into grids. (example image grids shape $7\times7$)
+2. Set anchors in the middle of each grid.
+3. For each grid:
+ - Using $B$ anchor boxes to regress $5$ numbers: $\text{dx, dy, dh, dw, confidence}$.
+ - Predict scores for each of $C$ classes.
+4. Finally the output is $7\times7\times(5B+C)$.
+
+
+
+### Instance Segmentation
+
+**Mask R-CNN:** Add a small mask network that operates on each RoI and predicts a $28\times28$ binary mask.
+
+
+
+Mask R-CNN performs very good results!
+
+
+
+## 10 - Recurrent Neural Networks
+
+Supplement content added according to [Deep Learning Book - RNN](https://www.deeplearningbook.org/contents/rnn.html).
+
+### Recurrent Neural Network (RNN)
+
+#### Motivation: Sequence Processing
+
+| One to One | One to Many | Many to One | Many to Many | Many to Many |
+| :--------------------------------------------------------: | :--------------------------------------------------------: | :--------------------------------------------------------: | :--------------------------------------------------------: | :----------------------------------------------------------: |
+|  |  |  |  |  |
+| Vanilla Neural Networks | Image Captioning | Action Prediction | Video Captioning | Video Classification on Frame Level |
+
+#### Vanilla RNN
+
+$x^{(t)}$ : Input at time $t$.
+
+$h^{(t)}$ : State at time $t$.
+
+$o^{(t)}$ : Output at time $t$.
+
+$y^{(t)}$ : Expected output at time $t$.
+
+##### Many to One
+
+
+
+| Calculation | |
+| ------------------ | ---------------------------------------------------- |
+| State Transition | $h^{(t)}=\tanh(Wh^{(t-1)}+Ux^{(t)}+b)$ |
+| Output Calculation | $o^{(\tau)}=\text{sigmoid}\ \big(Vh^{(\tau)}+c\big)$ |
+
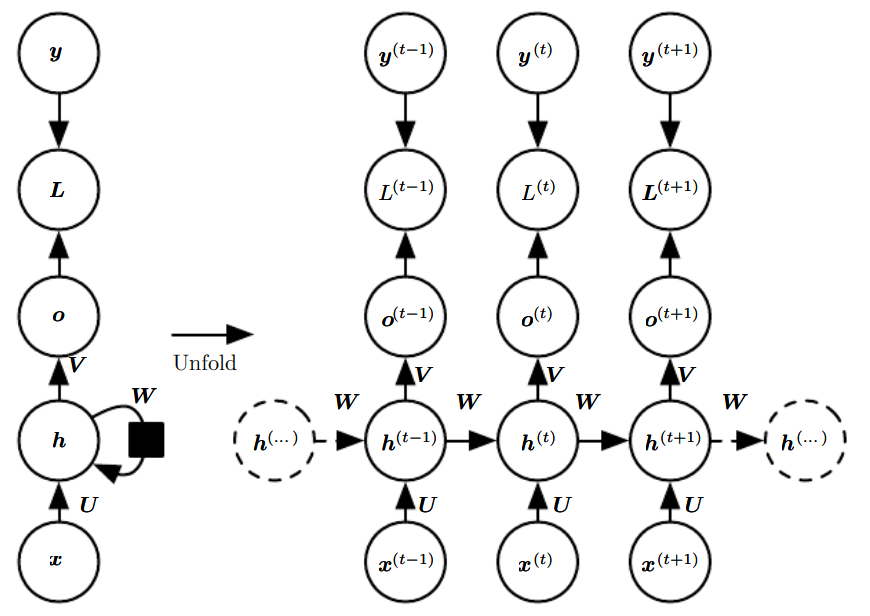
+##### Many to Many (type 2)
+
+
+
+| Calculation | |
+| ------------------ | ---------------------------------------------- |
+| State Transition | $h^{(t)}=\tanh(Wh^{(t-1)}+Ux^{(t)}+b)$ |
+| Output Calculation | $o^{(t)}=\text{sigmoid}\ \big(Vh^{(t)}+c\big)$ |
+
+#### RNN with Teacher Forcing
+
+Update current state according to last-time **output** instead of last-time **state**.
+
+
+
+| Calculation | |
+| ------------------ | ---------------------------------------------- |
+| State Transition | $h^{(t)}=\tanh(Wo^{(t-1)}+Ux^{(t)}+b)$ |
+| Output Calculation | $o^{(t)}=\text{sigmoid}\ \big(Vh^{(t)}+c\big)$ |
+
+#### RNN with "Output Forwarding"
+
+We can also combine last-state **output** with this-state **input** together.
+
+
+
+| Calculation | |
+| --------------------------- | ------------------------------------------------- |
+| State Transition (training) | $h^{(t)}=\tanh(Wh^{(t-1)}+Ux^{(t)}+Ry^{(t-1)}+b)$ |
+| State Transition (testing) | $h^{(t)}=\tanh(Wh^{(t-1)}+Ux^{(t)}+Ro^{(t-1)}+b)$ |
+| Output Calculation | $o^{(t)}=\text{sigmoid}\ \big(Vh^{(t)}+c\big)$ |
+
+Usually we use $o^{(t-1)}$ in place of $y^{(t-1)}$ at testing time.
+
+#### Bidirectional RNN
+
+When dealing with **a whole input sequence**, we can process features from two directions.
+
+
+
+| Calculation | |
+| --------------------------- | ------------------------------------------------------- |
+| State Transition (forward) | $h^{(t)}=\tanh(W_1h^{(t-1)}+U_1x^{(t)}+b_1)$ |
+| State Transition (backward) | $g^{(t)}=\tanh(W_2g^{(t+1)}+U_2x^{(t)}+b_2)$ |
+| Output Calculation | $o^{(t)}=\text{sigmoid}\ \big(Vh^{(t)}+Wg^{(t)}+c\big)$ |
+
+#### Encoder-Decoder Sequence to Sequence RNN
+
+This is a **many-to-many structure (type 1)**.
+
+First we encode information according to $x$ with no output.
+
+Later we decode information according to $y$ with no input.
+
+$C$ : Context vector, often $C=h^{(T)}$ (last state of encoder).
+
+
+
+| Calculation | |
+| ----------------------------------- | ----------------------------------------------- |
+| State Transition (encode) | $h^{(t)}=\tanh(W_1h^{(t-1)}+U_1x^{(t)}+b_1)$ |
+| State Transition (decode, training) | $s^{(t)}=\tanh(W_2s^{(t-1)}+U_2y^{(t)}+TC+b_2)$ |
+| State Transition (decode, testing) | $s^{(t)}=\tanh(W_2s^{(t-1)}+U_2o^{(t)}+TC+b_2)$ |
+| Output Calculation | $o^{(t)}=\text{sigmoid}\ \big(Vs^{(t)}+c\big)$ |
+
+#### Example: Image Captioning
+
+
+
+#### Summary
+
+**Advantages of RNN:**
+
+1. Can process any length input.
+2. Computation for step $t$ can (in theory) use information from many steps back.
+3. Model size doesn’t increase for longer input.
+4. Same weights applied on every timestep, so there is symmetry in how inputs are processed.
+
+**Disadvantages of RNN:**
+
+1. Recurrent computation is slow.
+2. In practice, difficult to access information from many steps back.
+3. Problems with gradient exploding and gradient vanishing. **(check [Deep Learning Book - RNN](https://www.deeplearningbook.org/contents/rnn.html) Page 396, Chap 10.7)**
+
+### Long Short Term Memory (LSTM)
+
+Add a "cell block" to store history weights.
+
+$c^{(t)}$ : Cell at time $t$.
+
+$f^{(t)}$ : **Forget gate** at time $t$. Deciding whether to erase the cell.
+
+$i^{(t)}$ : **Input gate** at time $t$. Deciding whether to write to the cell.
+
+$g^{(t)}$ : **External input gate** at time $t$. Deciding how much to write to the cell.
+
+$o^{(t)}$ : **Output gate** at time $t$. Deciding how much to reveal the cell.
+
+
+
+| Calculation (Gate) | |
+| ------------------- | ------------------------------------------------------------ |
+| Forget Gate | $f^{(t)}=\text{sigmoid}\ \big(W_fh^{(t-1)}+U_fx^{(t)}+b_f\big)$ |
+| Input Gate | $i^{(t)}=\text{sigmoid}\ \big(W_ih^{(t-1)}+U_ix^{(t)}+b_i\big)$ |
+| External Input Gate | $g^{(t)}=\tanh(W_gh^{(t-1)}+U_gx^{(t)}+b_g)$ |
+| Output Gate | $o^{(t)}=\text{sigmoid}\ \big(W_oh^{(t-1)}+U_ox^{(t)}+b_o\big)$ |
+
+| Calculation (Main) | |
+| ------------------ | ----------------------------------------------------- |
+| Cell Transition | $c^{(t)}=f^{(t)}\odot c^{(t-1)}+i^{(t)}\odot g^{(t)}$ |
+| State Transition | $h^{(t)}=o^{(t)}\odot\tanh(c^{(t)})$ |
+| Output Calculation | $O^{(t)}=\text{sigmoid}\ \big(Vh^{(t)}+c\big)$ |
+
+
+
+### Other RNN Variants
+
+GRU...
+
+## 11 - Attention and Transformers
+
+### RNN with Attention
+
+**Encoder-Decoder Sequence to Sequence RNN Problem:**
+
+Input sequence bottlenecked through a fixed-sized context vector $C$. (e.g. $T=1000$)
+
+
+
+**Intuitive Solution:**
+
+Generate new context vector $C_t$ at each step $t$ !
+
+$e_{t,i}$ : Alignment score for input $i$ at state $t$. **(scalar)**
+
+$a_{t,i}$ : Attention weight for input $i$ at state $t$.
+
+$C_t$ : Context vector at state $t$.
+
+
+
+
+
+| Calculation | |
+| ------------------------ | ------------------------------------------------------------ |
+| Alignment Score | $e_i^{(t)}=f(s^{(t-1)},h^{(i)})$.
Where $f$ is an MLP. |
+| Attention Weight | $a_i^{(t)}=\text{softmax}\ (e_i^{(t)})$.
Softmax includes all $e_i$ at state $t$. |
+| Context Vector | $C^{(t)}=\sum_i a_i^{(t)}h^{(i)}$ |
+| Decoder State Transition | $s^{(t)}=\tanh(Ws^{(t-1)}+Uy^{(t)}+TC^{(t)}+b)$ |
+
+**Example on Image Captioning:**
+
+
+
+
+
+### General Attention Layer
+
+Add linear transformations to the input vector before attention.
+
+
+
+**Notice:**
+
+1. Number of queries $q$ is variant. (can be **different** from the number of keys $k$)
+2. Number of outputs $y$ is equal to the number of queries $q$.
+
+ Each $y$ is a linear weighting of values $v$.
+
+3. Alignment $e$ is divided by $\sqrt{D}$ to avoid "explosion of softmax", where $D$ is the dimension of input feature.
+
+### Self-attention Layer
+
+The query vectors $q$ are also generated from the inputs.
+
+
+
+In this way, the shape of $y$ is equal to the shape of $x$.
+
+**Example with CNN:**
+
+
+
+### Positional Encoding
+
+Self-attention layer doesn’t care about the orders of the inputs!
+
+
+
+To encode ordered sequences like language or spatially ordered image features, we can add positional encoding to the inputs.
+
+
+
+We use a function $P:R\rightarrow R^d$ to process the **position** $i$ into a **d-dimensional vector** $p_i=P(i)$.
+
+| Constraint Condition of $P$ | |
+| --------------------------- | ---------------------------------------------------------- |
+| Uniqueness | $P(i)\ne P(j)$ |
+| Equidistance | $\lVert P(i+k)-P(i)\rVert^2=\lVert P(j+k)-P(j)\rVert^2$ |
+| Boundness | $P(i)\in[a,b]$ |
+| Determinacy | $P(i)$ is always a static value. (function is not dynamic) |
+
+We can either train a encoder model, or design a fixed function.
+
+**A Practical Positional Encoding Method:** Using $\sin$ and $\cos$ with different frequency $\omega$ at different dimension.
+
+$P(t)=\begin{bmatrix}\sin(\omega_1,t)\\\cos(\omega_1,t)\\\\\sin(\omega_2,t)\\\cos(\omega_2,t)\\\vdots\\\sin(\omega_{\frac{d}{2}},t)\\\cos(\omega_{\frac{d}{2}},t)\end{bmatrix}$, where frequency $\omega_k=\frac{1}{10000^{\frac{2k}{d}}}\\$. (wave length $\lambda=\frac{1}{\omega}=10000^{\frac{2k}{d}}\\$)
+
+$P(t)=\begin{bmatrix}\sin(1/10000^{\frac{2}{d}},t)\\\cos(1/10000^{\frac{2}{d}},t)\\\\\sin(1/10000^{\frac{4}{d}},t)\\\cos(1/10000^{\frac{4}{d}},t)\\\vdots\\\sin(1/10000^1,t)\\\cos(1/10000^1,t)\end{bmatrix}$, after we substitute $\omega_k$ into the equation.
+
+$P(t)$ is a vector with size $d$, where $d$ is a hyperparameter to choose according to the length of input sequence.
+
+An intuition of this method is the binary encoding of numbers.
+
+
+
+[[lecture 11d] 注意力和transformer (positional encoding 补充,代码实现,距离计算)](https://www.bilibili.com/video/BV1E3411B7Bz)
+
+**It is easy to prove that $P(t)$ satisfies "Equidistance":** (set $d=2$ for example)
+
+$\begin{aligned}\lVert P(i+k)-P(i)\rVert^2&=\big[\sin(\omega_1,i+k)-\sin(\omega_1,i)\big]^2+\big[\cos(\omega_1,i+k)-\cos(\omega_1,i)\big]^2\\&=2-2\sin(\omega_1,i+k)\sin(\omega_1,i)-2\cos(\omega_1,i+k)\cos(\omega_1,i)\\&=2-2\cos(\omega_1,k)\end{aligned}$
+
+So the distance is not associated with $i$, we have $\lVert P(i+k)-P(i)\rVert^2=\lVert P(j+k)-P(j)\rVert^2$.
+
+**Visualization of $P(t)$ features:** (set $d=32$, $x$ axis represents the position of sequence)
+
+
+
+### Masked Self-attention Layer
+
+To prevent vectors from looking at future vectors, we manually set alignment scores to $-\infty$.
+
+
+
+### Multi-head Self-attention Layer
+
+Multiple self-attention heads in parallel.
+
+
+
+### Transformer
+
+[Attention Is All You Need](https://arxiv.org/abs/1706.03762)
+
+#### Encoder Block
+
+**Inputs:** Set of vectors $z$. (in which $z_i$ can be a **word** in a sentence, or a **pixel** in a picture...)
+
+**Output:** Set of context vectors $c$. (encoded **features** of $z$)
+
+
+
+The number of blocks $N=6$ in original paper.
+
+**Notice:**
+
+1. Self-attention is the only interaction **between vectors** $x_0,x_1,\dots,x_n$.
+2. Layer norm and MLP operate independently **per vector**.
+3. Highly scalable, highly parallelizable, but high memory usage.
+
+#### Decoder Block
+
+**Inputs:** Set of vectors $y$. ($y_i$ can be a **word** in a sentence, or a **pixel** in a picture...)
+
+**Inputs:** Set of context vectors $c$.
+
+**Output:** Set of vectors $y'$. (decoded result, $y'_i=y_{i+1}$ for the first $n-1$ number of $y'$)
+
+
+
+The number of blocks $N=6$ in original paper.
+
+**Notice:**
+
+1. Masked self-attention only interacts with **past inputs**.
+2. Multi-head attention block is **NOT** self-attention. It attends over encoder outputs.
+3. Highly scalable, highly parallelizable, but high memory usage. (same as encoder)
+
+**Why we need mask in decoder:**
+
+1. Needs for the special formation of output $y'_i=y_{i+1}$.
+2. Needs for parallel computation.
+
+[举个例子讲下transformer的输入输出细节及其他](https://zhuanlan.zhihu.com/p/166608727)
+
+[在测试或者预测时,Transformer里decoder为什么还需要seq mask?](https://blog.csdn.net/season77us/article/details/104144613)
+
+#### Example on Image Captioning (Only with Transformers)
+
+
+
+### Comparing RNNs to Transformer
+
+| | RNNs | Transformer |
+| -------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
+| **Pros** | LSTMs work reasonably well for **long sequences**. | 1. Good at **long sequences**. Each attention calculation looks at all inputs.
2. Can operate over unordered sets or **ordered sequences** with positional encodings.
3. **Parallel computation:** All alignment and attention scores for all inputs can be done in parallel. |
+| **Cons** | 1. Expects an **ordered sequences** of inputs.
2. **Sequential computation:** Subsequent hidden states can only be computed after the previous ones are done. | **Requires a lot of memory:** $N\times M$ alignment and attention scalers need to be calculated and stored for a single self-attention head. |
+
+### Comparing ConvNets to Transformer
+
+ConvNets strike back!
+
+
+
+## 12 - Video Understanding
+
+### Video Classification
+
+Take video classification task for example.
+
+
+
+Input size: $C\times T\times H\times W$.
+
+The problem is, videos are quite big. We can't afford to train on raw videos, instead we train on video clips.
+
+| Raw Videos | Video Clips |
+| ------------------------------- | -------------------------------------- |
+| $1920\times1080,\ 30\text{fps}$ | $112\times112,\ 5\text{f}/3.2\text{s}$ |
+| $10\text{GB}/\text{min}$ | $588\text{KB}/\text{min}$ |
+
+
+
+### Plain CNN Structure
+
+#### Single Frame 2D-CNN
+
+Train a normal 2D-CNN model.
+
+Classify each frame independently.
+
+Average the result of each frame as the final result.
+
+
+
+#### Late Fusion
+
+Get high-level appearance of each frame, and combine them.
+
+Run 2D-CNN on each frame, pool features and feed to Linear Layers.
+
+
+
+**Problem:** Hard to compare low-level motion between frames.
+
+
+
+#### Early Fusion
+
+Compare frames with very first Conv Layer, after that normal 2D-CNN.
+
+
+
+**Problem:** One layer of temporal processing may not be enough!
+
+#### 3D-CNN
+
+**Convolve on 3 dimensions:** Height, Width, Time.
+
+**Input size:** $C_{in}\times T\times H\times W$.
+
+**Kernel size:** $C_{in}\times C_{out}\times 3\times 3\times 3$.
+
+**Output size:** $C_{out}\times T\times H\times W$. (with zero paddling)
+
+
+
+#### C3D (VGG of 3D-CNNs)
+
+The cost is quite expensive...
+
+| Network | Calculation |
+| ------- | -------------- |
+| AlexNet | 0.7 GFLOP |
+| VGG-16 | 13.6 GFLOP |
+| C3D | **39.5** GFLOP |
+
+#### Two-Stream Networks
+
+Separate motion and appearance.
+
+
+
+#### I3D (Inflating 2D Networks to 3D)
+
+Take a 2D-CNN architecture.
+
+Replace each 2D conv/pool layer with a 3D version.
+
+
+
+### Modeling Long-term Temporal Structure
+
+#### Recurrent Convolutional Network
+
+Similar to multi-layer RNN, we replace the **dot-product** operation with **convolution**.
+
+
+
+Feature size in layer $L$, time $t-1$: $W_h\times H\times W$.
+
+Feature size in layer $L-1$, time $t$: $W_x\times H\times W$.
+
+Feature size in layer $L$, time $t$: $(W_h+W_x)\times H\times W$.
+
+
+
+**Problem:** RNNs are slow for long sequences. (can’t be parallelized)
+
+#### Spatio-temporal Self-attention
+
+Introduce self-attention into video classification problems.
+
+
+
+
+
+#### Vision Transformers for Video
+
+Factorized attention: Attend over space / time.
+
+So many papers...
+
+
+
+### Visualizing Video Models
+
+
+
+
+
+### Multimodal Video Understanding
+
+#### Temporal Action Localization
+
+Given a long untrimmed video sequence, identify frames corresponding to different actions.
+
+
+
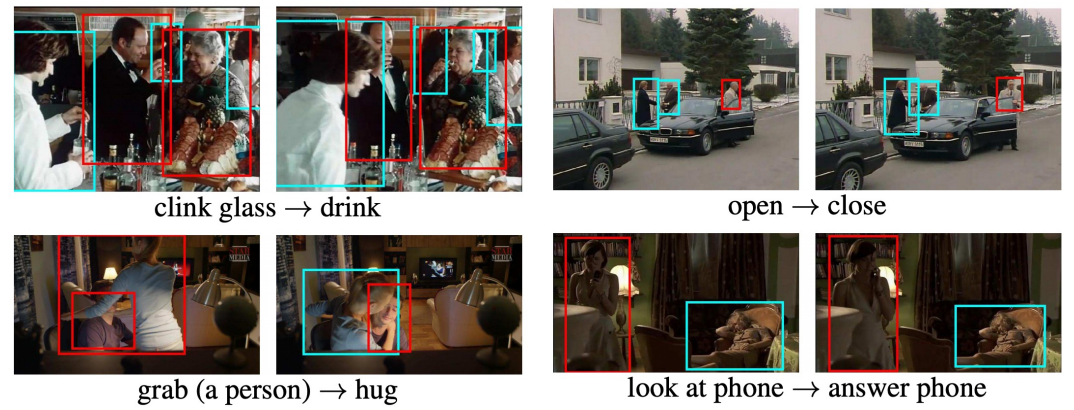
+#### Spatio-Temporal Detection
+
+Given a long untrimmed video, detect all the people in both space and time and classify the activities they are performing.
+
+
+
+#### Visually-guided Audio Source Separation
+
+
+
+And So on...
+
+## 13 - Generative Models
+
+
+
+### PixelRNN and PixelCNN
+
+#### Fully Visible Belief Network (FVBN)
+
+$p(x)$ : Likelihood of image $x$.
+
+$p(x_1,x_2,\dots,x_n)$ : Joint likelihood of all $n$ pixels in image $x$.
+
+$p(x_i|x_1,x_2,\dots,x_{i-1})$ : Probability of pixel $i$ value given all previous pixels.
+
+For explicit density models, we have $p(x)=p(x_1,x_2,\dots,x_n)=\prod_{i=1}^np(x_i|x_1,x_2,\dots,x_{i-1})\\$.
+
+**Objective:** Maximize the likelihood of training data.
+
+
+
+#### PixelRNN
+
+Generate image pixels starting from corner.
+
+Dependency on previous pixels modeled using an RNN (LSTM).
+
+**Drawback:** Sequential generation is slow in both training and inference!
+
+
+
+#### PixelCNN
+
+Still generate image pixels starting from corner.
+
+Dependency on previous pixels modeled using a CNN over context region (masked convolution).
+
+**Drawback:** Though its training is faster, its generation is still slow. **(pixel by pixel)**
+
+
+
+### Variational Autoencoder
+
+Supplement content added according to [Tutorial on Variational Autoencoders](https://arxiv.org/abs/1606.05908). (**paper with notes:** [VAE Tutorial.pdf](..\Variational Autoencoder\papes\VAE Tutorial.pdf))
+
+[变分自编码器VAE:原来是这么一回事 | 附开源代码](https://zhuanlan.zhihu.com/p/34998569)
+
+#### Autoencoder
+
+Learn a lower-dimensional feature representation with unsupervised approaches.
+
+$x\rightarrow z$ : Dimension reduction for input features.
+
+$z\rightarrow \hat{x}$ : Reconstruct input features.
+
+
+
+After training, we throw the decoder away and use the encoder for transferring.
+
+
+
+**For generative models, there is a problem:**
+
+We can’t generate new images from an autoencoder because we don’t know the space of $z$.
+
+#### Variational Autoencoder
+
+##### Character Description
+
+$X$ : Images. **(random variable)**
+
+$Z$ : Latent representations. **(random variable)**
+
+$P(X)$ : True distribution of all training images $X$.
+
+$P(Z)$ : True distribution of all latent representations $Z$.
+
+$P(X|Z)$ : True **posterior** distribution of all images $X$ with condition $Z$.
+
+$P(Z|X)$ : True **prior** distribution of all latent representations $Z$ with condition $X$.
+
+$Q(Z|X)$ : Approximated **prior** distribution of all latent representations $Z$ with condition $X$.
+
+$x$ : A specific image.
+
+$z$ : A specific latent representation.
+
+$\theta$: Learned parameters in decoder network.
+
+$\phi$: Learned parameters in encoder network.
+
+$p_\theta(x)$ : Probability that $x\sim P(X)$.
+
+$p_\theta(z)$ : Probability that $z\sim P(Z)$.
+
+$p_\theta(x|z)$ : Probability that $x\sim P(X|Z)$.
+
+$p_\theta(z|x)$ : Probability that $z\sim P(Z|X)$.
+
+$q_\phi(z|x)$ : Probability that $z\sim Q(Z|X)$.
+
+##### Decoder
+
+**Objective:**
+
+Generate new images from $\mathscr{z}$.
+
+1. Generate a value $z^{(i)}$ from the prior distribution $P(Z)$.
+2. Generate a value $x^{(i)}$ from the conditional distribution $P(X|Z)$.
+
+**Lemma:**
+
+Any distribution in $d$ dimensions can be generated by taking a set of $d$ variables that are **normally distributed** and mapping them through a sufficiently complicated function. (source: [Tutorial on Variational Autoencoders](https://arxiv.org/abs/1606.05908), Page 6)
+
+**Solutions:**
+
+1. Choose prior distribution $P(Z)$ to be a simple distribution, for example $P(Z)\sim N(0,1)$.
+2. Learn the conditional distribution $P(X|Z)$ through a neural network (decoder) with parameter $\theta$.
+
+
+
+##### Encoder
+
+**Objective:**
+
+Learn $\mathscr{z}$ with training images.
+
+**Given:** (From the decoder, we can deduce the following probabilities.)
+
+1. *data likelihood:* $p_\theta(x)=\int p_\theta(x|z)p_\theta(z)dz$.
+2. *posterior density:* $p_\theta(z|x)=\frac{p_\theta(x|z)p_\theta(z)}{p_\theta(x)}=\frac{p_\theta(x|z)p_\theta(z)}{\int p_\theta(x|z)p_\theta(z)dz}$.
+
+**Problem:**
+
+Both $p_\theta(x)$ and $p_\theta(z|x)$ are intractable. (can't be optimized directly as they contain *integral operation*)
+
+**Solution:**
+
+Learn $Q(Z|X)$ to approximate the true posterior $P(Z|X)$.
+
+Use $q_\phi(z|x)$ in place of $p_\theta(z|x)$.
+
+
+
+##### Variational Autoencoder (Combination of Encoder and Decoder)
+
+**Objective:**
+
+Maximize $p_\theta(x)$ for all $x^{(i)}$ in the training set.
+
+$$
+\begin{aligned}
+\log p_\theta\big(x^{(i)}\big)&=\mathbb{E}_{z\sim q_\phi\big(z|x^{(i)}\big)}\Big[\log p_\theta\big(x^{(i)}\big)\Big]\\
+
+&=\mathbb{E}_z\Bigg[\log\frac{p_\theta\big(x^{(i)}|z\big)p_\theta\big(z\big)}{p_\theta\big(z|x^{(i)}\big)}\Bigg]\quad\text{(Bayes' Rule)}\\
+
+&=\mathbb{E}_z\Bigg[\log\frac{p_\theta\big(x^{(i)}|z\big)p_\theta\big(z\big)}{p_\theta\big(z|x^{(i)}\big)}\frac{q_\phi\big(z|x^{(i)}\big)}{q_\phi\big(z|x^{(i)}\big)}\Bigg]\quad\text{(Multiply by Constant)}\\
+
+&=\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]-\mathbb{E}_z\Bigg[\log\frac{q_\phi\big(z|x^{(i)}\big)}{p_\theta\big(z\big)}\Bigg]+\mathbb{E}_z\Bigg[\log\frac{p_\theta\big(z|x^{(i)}\big)}{q_\phi\big(z|x^{(i)}\big)}\Bigg]\quad\text{(Logarithm)}\\
+
+&=\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]-D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]+D_{\text{KL}}\Big[p_\theta\big(z|x^{(i)}\big)||q_\phi\big(z|x^{(i)}\big)\Big]\quad\text{(KL Divergence)}
+\end{aligned}
+$$
+
+**Analyze the Formula by Term:**
+
+$\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]$: Decoder network gives $p_\theta\big(x^{(i)}|z\big)$, can compute estimate of this term through sampling.
+
+$D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]$: This KL term (between Gaussians for encoder and $z$ prior) has nice closed-form solution!
+
+$D_{\text{KL}}\Big[p_\theta\big(z|x^{(i)}\big)||q_\phi\big(z|x^{(i)}\big)\Big]$: The part $p_\theta\big(z|x^{(i)}\big)$ is intractable. **However, we know KL divergence always $\ge0$.**
+
+**Tractable Lower Bound:**
+
+We can maximize the lower bound of that formula.
+
+As $D_{\text{KL}}\Big[p_\theta\big(z|x^{(i)}\big)||q_\phi\big(z|x^{(i)}\big)\Big]\ge0$ , we can deduce that:
+
+$$
+\begin{aligned}
+\log p_\theta\big(x^{(i)}\big)&=\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]-D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]+D_{\text{KL}}\Big[p_\theta\big(z|x^{(i)}\big)||q_\phi\big(z|x^{(i)}\big)\Big]\\
+
+&\ge\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]-D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]
+\end{aligned}
+$$
+
+So the loss function $\mathcal{L}\big(x^{(i)},\theta,\phi\big)=-\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]+D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]$.
+
+$\mathbb{E}_z\Big[\log p_\theta\big(x^{(i)}|z\big)\Big]$: ***Decoder***, reconstruct the input data.
+
+$D_{\text{KL}}\Big[q_\phi\big(z|x^{(i)}\big)||p_\theta\big(z\big)\Big]$: ***Encoder***, make approximate posterior distribution close to prior.
+
+
+
+### Generative Adversarial Networks (GANs)
+
+#### Motivation & Modeling
+
+**Objective:** Not modeling any explicit density function.
+
+**Problem:** Want to sample from complex, high-dimensional training distribution. **No direct way to do this!**
+
+**Solution:** Sample from a simple distribution, e.g. **random noise**. Learn the transformation to training distribution.
+
+
+
+**Problem:** We can't learn the **mapping relation** between sample $z$ and training images.
+
+**Solution:** Use a **discriminator network** to tell whether the generate image is within data distribution or not.
+
+
+
+**Discriminator network:** Try to distinguish between real and fake images.
+
+**Generator network:** Try to fool the discriminator by generating real-looking images.
+
+
+
+$x$ : Real data.
+
+$y$ : Fake data, which is generated by the generator network. $y=G_{\theta_g}(z)$.
+
+$D_{\theta_d}(x)$ : Discriminator score, which is the likelihood of real image. $D_{\theta_d}(x)\in[0,1]$.
+
+**Objective of discriminator network:**
+
+$\max_{\theta_d}\bigg[\mathbb{E}_x\Big(\log D_{\theta_d}(x)\Big)+\mathbb{E}_{z\sim p(z)}\Big(\log\big(1-D_{\theta_d}(y)\big)\Big)\bigg]$
+
+**Objective of generator network:**
+
+$\min_{\theta_g}\max_{\theta_d}\bigg[\mathbb{E}_x\Big(\log D_{\theta_d}(x)\Big)+\mathbb{E}_{z\sim p(z)}\Big(\log\big(1-D_{\theta_d}(y)\big)\Big)\bigg]$
+
+#### Training Strategy
+
+Two combine this two networks together, we can train them alternately:
+
+1. Gradient **ascent** on discriminator.
+
+ $\max_{\theta_d}\bigg[\mathbb{E}_x\Big(\log D_{\theta_d}(x)\Big)+\mathbb{E}_{z\sim p(z)}\Big(\log\big(1-D_{\theta_d}(y)\big)\Big)\bigg]$
+
+2. Gradient **descent** on generator.
+
+ $\min_{\theta_g}\bigg[\mathbb{E}_{z\sim p(z)}\Big(\log\big(1-D_{\theta_d}(y)\big)\Big)\bigg]$
+
+However, the gradient of generator decreases with the value itself, making it **hard to optimize**.
+
+
+
+So we replace $\log\big(1-D_{\theta_d}(y)\big)$ with $-\log D_{\theta_d}(y)$, and use gradient ascent instead.
+
+1. Gradient **ascent** on discriminator.
+
+ $\max_{\theta_d}\bigg[\mathbb{E}_x\Big(\log D_{\theta_d}(x)\Big)+\mathbb{E}_{z\sim p(z)}\Big(\log\big(1-D_{\theta_d}(y)\big)\Big)\bigg]$
+
+2. Gradient **ascent** on generator.
+
+ $\max_{\theta_g}\bigg[\mathbb{E}_{z\sim p(z)}\Big(\log D_{\theta_d}(y)\Big)\bigg]$
+
+#### Summary
+
+**Pros:** Beautiful, state-of-the-art samples!
+
+**Cons:**
+
+1. Trickier / more unstable to train.
+2. Can’t solve inference queries such as $p(x), p(z|x)$.
+
+## 14 - Self-supervised Learning
+
+**Aim:** Solve “pretext” tasks that produce good features for downstream tasks.
+
+**Application:**
+
+1. Learn a feature extractor from pretext tasks. **(self-supervised)**
+2. Attach a shallow network on the feature extractor.
+3. Train the shallow network on target task with small amount of labeled data. **(supervised)**
+
+
+
+### Pretext Tasks
+
+Labels are generated automatically.
+
+#### Rotation
+
+ Train a classifier on randomly rotated images.
+
+
+
+#### Rearrangement
+
+Train a classifier on randomly shuffled image pieces.
+
+Predict the location of image pieces.
+
+
+
+#### Inpainting
+
+Mask part of the image, train a network to predict the masked area.
+
+Method referencing [Context Encoders: Feature Learning by Inpainting](https://arxiv.org/pdf/1604.07379.pdf).
+
+Combine two types of loss together to get better performance:
+
+1. **Reconstruction loss (L2 loss):** Used for reconstructing global features.
+2. **Adversarial loss:** Used for generating texture features.
+
+
+
+#### Coloring
+
+Transfer between greyscale images and colored images.
+
+**Cross-channel predictions for images:** [Split-Brain Autoencoders](https://openaccess.thecvf.com/content_cvpr_2017/papers/Zhang_Split-Brain_Autoencoders_Unsupervised_CVPR_2017_paper.pdf).
+
+
+
+**Video coloring:** Establish mappings between reference and target frames in a learned feature space. [Tracking Emerges by Colorizing Videos](https://arxiv.org/abs/1806.09594).
+
+
+
+#### Summary for Pretext Tasks
+
+1. Pretext tasks focus on **“visual common sense”**.
+2. The models are forced learn good features about natural images.
+3. We **don’t** care about the performance of these **pretext tasks**.
+
+ What we care is the performance of **downstream tasks**.
+
+#### Problems of Specific Pretext Tasks
+
+1. Coming up with **individual** pretext tasks is tedious.
+2. The learned representations may **not be general**.
+
+**Intuitive Solution:** Contrastive Learning.
+
+### Contrastive Representation Learning
+
+**Local additional references:** [Contrastive Learning.md](..\..\DL\Contrastive Learning\Contrastive Learning.md).
+
+
+
+**Objective:**
+
+Given a chosen score function $s$, we aim to learn an encoder function $f$ that yields:
+
+1. For each sample $x$, increase the similarity $s\big(f(x),f(x^+)\big)$ between $x$ and positive samples $x^+$.
+2. Finally we want $s\big(f(x),f(x^+)\big)\gg s\big(f(x),f(x^-)\big)$.
+
+**Loss Function:**
+
+Given $1$ positive sample and $N-1$ negative samples:
+
+| InfoNCE Loss | Cross Entropy Loss |
+| ------------------------------------------------------------ | ------------------------------------------------------------ |
+| $\begin{aligned}\mathcal{L}=-\mathbb{E}_X\Bigg[\log\frac{\exp{s\big(f(x),f(x^+)\big)}}{\exp{s\big(f(x),f(x^+)\big)}+\sum_{j=1}^{N-1}\exp{s\big(f(x),f(x^+)\big)}}\Bigg]\\\end{aligned}$ | $\begin{aligned}\mathcal{L}&=-\sum_{i=1}^Np(x_i)\log q(x_i)\\&=-\mathbb{E}_X\big[\log q(x)\big]\\&=-\mathbb{E}_X\Bigg[\log\frac{\exp(x)}{\sum_{j=1}^N\exp(x_j)}\Bigg]\end{aligned}$ |
+
+The *InfoNCE Loss* is a lower bound on the *mutual information* between $f(x)$ and $f(x^+)$:
+
+$\text{MI}\big[f(x),f(x^+)\big]\ge\log(N)-\mathcal{L}$
+
+The *larger* the negative sample size $N$, the *tighter* the bound.
+
+So we use $N-1$ negative samples.
+
+#### Instance Contrastive Learning
+
+##### [SimCLR](https://arxiv.org/pdf/2002.05709.pdf)
+
+Use a projection function $g(\cdot)$ to project features to a space where contrastive learning is applied.
+
+The extra projection contributes a lot to the final performance.
+
+
+
+**Score Function:** Cos similarity $s(u,v)=\frac{u^Tv}{||u||||v||}\\$.
+
+**Positive Pair:** Pair of augmented data.
+
+
+
+##### [Momentum Contrastive Learning (MoCo)](https://arxiv.org/pdf/1911.05722.pdf)
+
+There are mainly $3$ training strategy in contrastive learning:
+
+1. *end-to-end:* Keys are updated together with queries, e.g. ***SimCLR***.
+
+ **(limited by GPU size)**
+
+2. *memory bank:* Store last-time keys for sampling.
+
+ **(inconsistency between $q$ and $k$)**
+
+3. ***MoCo**:* Use momentum methods to encode keys.
+
+ **(combination of *end-to-end* & *memory bank*)**
+
+
+
+**Key differences to SimCLR:**
+
+1. Keep a running **queue** of keys (negative samples).
+2. Compute gradients and update the encoder **only through the queries**.
+3. Decouple min-batch size with the number of keys: can support **a large number of negative samples**.
+4. The key encoder is **slowly progressing** through the momentum update rules:
+
+ $\theta_k\leftarrow m\theta_k+(1-m)\theta_q$
+
+
+
+#### Sequence Contrastive Learning
+
+##### Contrastive Predictive Coding (CPC)
+
+**Contrastive:** Contrast between “right” and “wrong” sequences using contrastive learning.
+
+**Predictive:** The model has to *predict* future patterns given the current context.
+
+**Coding:** The model learns useful *feature vectors*, or “code”, for downstream tasks, similar to other self-supervised methods.
+
+
+
+#### Other Examples (Frontier)
+
+##### Contrastive Language Image Pre-training (CLIP)
+
+Contrastive learning between image and natural language sentences.
+
+
+
+## 15 - Low-Level Vision
+
+Pass...
+
+## 16 - 3D Vision
+
+### Representation
+
+#### Explicit vs Implicit
+
+**Explicit:** Easy to sample examples, hard to do inside/outside check.
+
+**Implicit:** Hard to sample examples, easy to do inside/outside check.
+
+| | Non-parametric | Parametric |
+| ------------ | ---------------------- | --------------------------------------------------- |
+| **Explicit** | Points.
Meshes. | Splines.
Subdivision Surfaces. |
+| **Implicit** | Level Sets.
Voxels. | Algebraic Surfaces.
Constructive Solid Geometry. |
+
+#### Point Clouds
+
+The simplest representation.
+
+Collection of $(x,y,z)$ coordinates.
+
+**Cons:**
+
+1. Difficult to draw in under-sampled regions.
+2. No simplification or subdivision.
+3. No direction smooth rendering.
+4. No topological information.
+
+
+
+#### Polygonal Meshes
+
+Collection of vertices $v$ and edges $e$.
+
+**Pros:**
+
+1. Can apply downsampling or upsampling on meshes.
+2. Error decreases by $O(n^2)$ while meshes increase by $O(n)$.
+3. Can approximate arbitrary topology.
+4. Efficient rendering.
+
+
+
+#### Splines
+
+Use specific functions to approximate the surface. (e.g. Bézier Curves)
+
+
+
+#### Algebraic Surfaces
+
+Use specific functions to represent the surface.
+
+
+
+#### Constructive Solid Geometry
+
+Combine implicit geometry with Boolean operations.
+
+
+
+#### Level Sets
+
+Store a grim of values to approximate the function.
+
+Surface is found where interpolated value equals to $0$.
+
+
+
+#### Voxels
+
+Binary thresholding the volumetric grid.
+
+
+
+### AI + 3D
+
+Pass...