index.md

110. Balanced Binary Tree

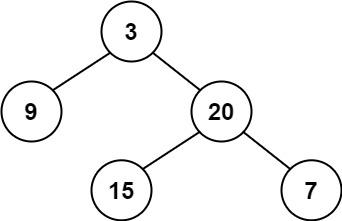
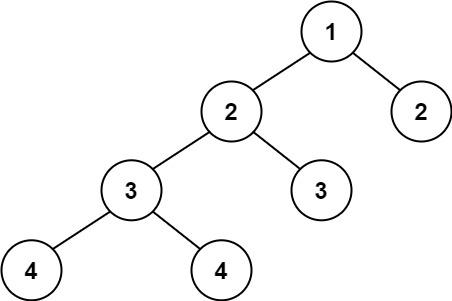
Given a binary tree, determine if it is height-balanced.

Example 1:

Input: root = [3,9,20,null,null,15,7] Output: true

Example 2:

Input: root = [1,2,2,3,3,null,null,4,4] Output: false

Example 3:

Input: root = [] Output: true

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -104 <= Node.val <= 104

Solution

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        def check(node):
            if not node:
                return 0

            left_height = check(node.left)
            right_height = check(node.right)

            # If the subtree is not balanced, return -1
            if left_height == -1 or right_height == -1 or abs(left_height - right_height) > 1:
                return -1

            return 1 + max(left_height, right_height)

        return check(root) != -1

Thoughts

Time Complexity

The time complexity is O(n), where n is the number of nodes in the tree. This is because we visit each node exactly once in the recursive traversal.

Space Complexity

The space complexity is O(h), where h is the height of the tree. This is due to the recursive call stack. In the worst case, the tree could be linear (i.e., a linked list), in which case the height of the tree would be equal to the number of nodes, leading to a space complexity of O(n).