readme.md

230. Kth Smallest Element in a BST

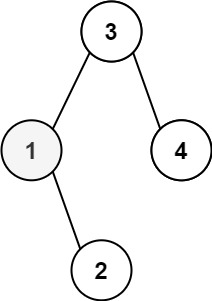
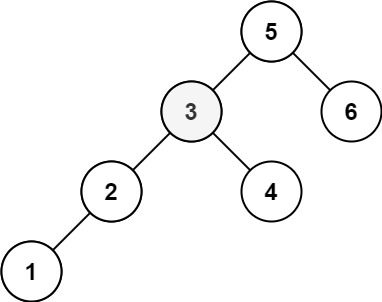
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

Input: root = [3,1,4,null,2], k = 1

Output: 1

Example 2:

Input: root = [5,3,6,2,4,null,null,1], k = 3

Output: 3

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

Solution

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        self.count = 0
        def inOrderTraversal(node):
            if not node:
                return None

            # Traverse the left subtree
            left = inOrderTraversal(node.left)
            if left is not None:
                return left

            # Visit the node
            self.count += 1
            if self.count == k:
                return node.val

            # Traverse the right subtree
            return inOrderTraversal(node.right)

        return inOrderTraversal(root)

Thoughts

Time Complexity

The time complexity of this solution is O(n) in the worst case, where n is the number of nodes in the tree. This is because we might need to visit all nodes in the tree if k is equal to n.

Space Complexity

The space complexity of this solution is O(h), where h is the height of the tree. This is because the maximum amount of space utilized by the recursion stack would be equal to the height of the tree. In the worst case, the tree is a linear chain (i.e., each node has only one child), and the height of the tree is O(n). In the best case, the tree is completely balanced, and the height of the tree is O(log n).

Follow-up

For the follow-up question, if the BST is modified often and we need to find the kth smallest frequently, we can optimize by:

Augmenting the Tree Structure: Store the size of the subtree rooted at each node. This allows us to quickly determine the rank of each node in the sorted order. When inserting or deleting nodes, update the subtree sizes accordingly.

Balanced BST: Use a self-balancing BST like AVL or Red-Black Tree to ensure that the height of the tree remains O(log n), which keeps insertions, deletions, and lookups efficient.

With these optimizations, finding the kth smallest element can be done in O(log n) time, where n is the number of nodes in the tree.