readme.md

695. Max Area of Island

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

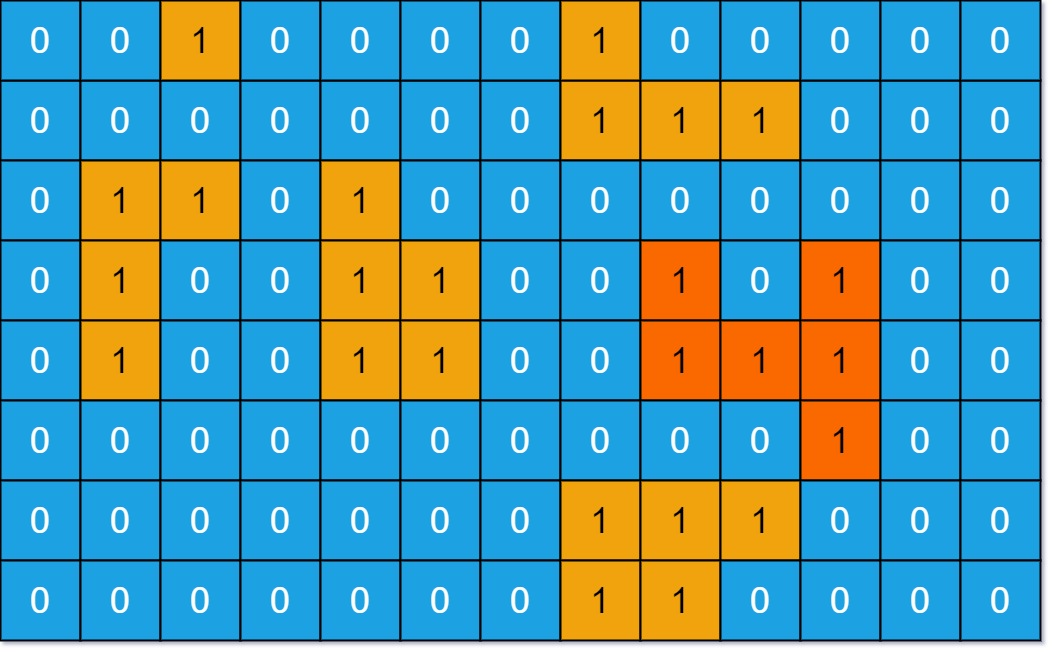
**Input:** grid = [
    [0,0,1,0,0,0,0,1,0,0,0,0,0],
    [0,0,0,0,0,0,0,1,1,1,0,0,0],
    [0,1,1,0,1,0,0,0,0,0,0,0,0],
    [0,1,0,0,1,1,0,0,1,0,1,0,0],
    [0,1,0,0,1,1,0,0,1,1,1,0,0],
    [0,0,0,0,0,0,0,0,0,0,1,0,0],
    [0,0,0,0,0,0,0,1,1,1,0,0,0],
    [0,0,0,0,0,0,0,1,1,0,0,0,0]
    ]

Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• grid[i][j] is either 0 or 1.

Solution

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        def dfs(row, col):
            if 0 <= row < len(grid) and 0 <= col < len(grid[0]) and grid[row][col] == 1:
                grid[row][col] = 0  # Mark as visited
                return 1 + dfs(row + 1, col) + dfs(row - 1, col) + dfs(row, col + 1) + dfs(row, col - 1)
            return 0

        max_area = 0
        for row in range(len(grid)):
            for col in range(len(grid[0])):
                if grid[row][col] == 1:
                    max_area = max(max_area, dfs(row, col))
        return max_area

Thoughts

Time Complexity

The time complexity is O(M * N), where M is the number of rows and N is the number of columns in the grid. This is because, in the worst case, we might need to visit every cell in the grid once.

Space Complexity

The space complexity is O(M * N) in the worst case for the recursion stack, in case the grid is filled with land cells. However, this can be considered O(1) if we assume the recursion stack size is limited by the system.