index.md

74. Search a 2D Matrix

You are given an m x n integer matrix matrix with the following two properties:

• Each row is sorted in non-decreasing order.
• The first integer of each row is greater than the last integer of the previous row.

Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n)) time complexity.

Example 1:

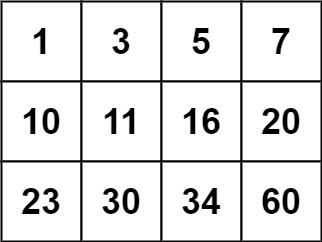
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 Output: true

Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Solution

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix or not matrix[0]:
            return False

        rows, cols = len(matrix), len(matrix[0])
        left, right = 0, rows * cols - 1

        while left <= right:
            mid = (left + right) // 2
            mid_value = matrix[mid // cols][mid % cols]  # Convert 1D index to 2D indices

            if mid_value == target:
                return True
            elif mid_value < target:
                left = mid + 1
            else:
                right = mid - 1

        return False

Thoughts

The time complexity of this algorithm is O(log(m * n)) since it is essentially a binary search. The space complexity is O(1), as we are not using any additional data structures that grow with the size of the input.