index.md

84. Largest Rectangle in Histogram

Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

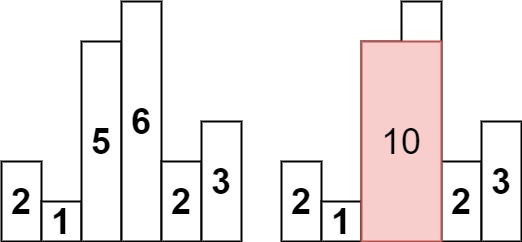
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

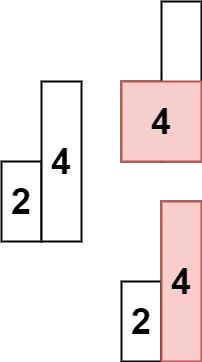
Input: heights = [2,4] Output: 4

Constraints:

• 1 <= heights.length <= 105
• 0 <= heights[i] <= 104

Solution

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        # Initialize the maximum area to 0
        maxArea = 0
        # Initialize the stack that will store tuples of (index, height)
        stack = []  

        # Iterate through each bar in the histogram
        for i, h in enumerate(heights):
            # Initialize the start variable which denotes the start of a rectangle
            start = i
            # While the stack is not empty and the current height is less than the height at the top of the stack
            while stack and stack[-1][1] > h:
                # Pop the stack and calculate the area of the rectangle
                # using the height of the popped bar and width as the current index minus the popped index
                index, height = stack.pop()
                maxArea = max(maxArea, height * (i - index))
                # Update start to the index of the popped bar
                start = index
            # Append the current bar as the potential start of a new rectangle
            stack.append((start, h))

        # After we finish going through all the bars,
        # we may have some bars left in the stack that could form rectangles extending to the end of the histogram
        for i, h in stack:
            # The width is the total width of the histogram minus the index where the bar started
            maxArea = max(maxArea, h * (len(heights) - i))

        # Return the maximum area found
        return maxArea

Thoughts

The solution has a time complexity of O(n), as each bar is pushed and popped from the stack exactly once. The space complexity is O(n) due to the stack used to store the indices and heights of the bars.