readme.md

97. Interleaving String

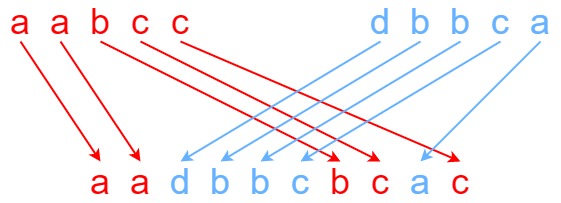
Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m

substrings

respectively, such that:

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" Output: true Explanation: One way to obtain s3 is: Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a". Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac". Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" Output: false Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = "" Output: true

Constraints:

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Solution

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n, o = len(s1), len(s2), len(s3)
        if m + n != o:
            return False

        dp = [[False] * (n + 1) for _ in range(m + 1)]
        dp[0][0] = True

        # populate the base condition using only s1
        for i in range(1, m + 1):
            dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]

        for j in range(1, n + 1):
            dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                dp[i][j] = (dp[i - 1][j] and s1[i - 1] == s3[i + j - 1]) or \
                           (dp[i][j - 1] and s2[j - 1] == s3[i + j - 1])

        return dp[m][n]

Thoughts

Time Complexity

• O(m * n), where m is the length of s1 and n is the length of s2. We iterate over all states (i.e., pairs (i, j)) to fill the DP table.

Space Complexity

• O(m * n) for the DP table. We can optimize this to O(min(m, n)) by only keeping the current and previous rows (or columns) if s2 is shorter.

Space optimised solution

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        # Check if the total lengths are mismatched, if so, it cannot be interleaved to form s3.
        if len(s1) + len(s2) != len(s3):
            return False

        # If s2 is longer than s1, swap them to minimize the space used in DP.
        if len(s2) > len(s1):
            s1, s2 = s2, s1

        # Initialize the DP array with False values, plus one for zero index (no characters taken from s2).
        dp = [False] * (len(s2) + 1)
        dp[0] = True  # Base case: an empty s1 and s2 trivially form an empty s3.

        # Initialize the DP array for the case when s1 is empty.
        for j in range(1, len(s2) + 1):
            dp[j] = dp[j - 1] and s2[j - 1] == s3[j - 1]

        # Iterate through characters of s1
        for i in range(1, len(s1) + 1):
            # Update dp[0] for the current row, using characters only from s1 up to i
            dp[0] = dp[0] and s1[i - 1] == s3[i - 1]

            # Iterate through characters of s2
            for j in range(1, len(s2) + 1):
                # dp[j] is True if:
                # 1. dp[j] was True and the next character of s1 matches the corresponding character in s3
                # 2. dp[j-1] was True and the next character of s2 matches the corresponding character in s3
                dp[j] = (dp[j] and s1[i - 1] == s3[i + j - 1]) or \
                        (dp[j - 1] and s2[j - 1] == s3[i + j - 1])

        # The result for the whole s3 being an interleave of s1 and s2 is found at dp[len(s2)]
        return dp[len(s2)]