Create Red-Black Tree와 java.util에서의 구현 1.md

binary-ho · Apr 2, 2024 · 0268bd8 · 0268bd8
1 parent 4f00984
commit 0268bd8
Showing 1 changed file with 138 additions and 0 deletions.
diff --git a/Red-Black Tree와 java.util에서의 구현 1.md b/Red-Black Tree와 java.util에서의 구현 1.md
@@ -0,0 +1,138 @@
+# Red-Black Tree와 java.util에서의 구현 방식 1
+- 1편 : Red-Black Tree란?
+- 2편 : java.util에서의 구현 코드로 이해하는 Red-Black Tree
+
+## 1. Red-Black Tree란
+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/b5492724-25b2-48ce-8854-c10f731f6e5c)
+
+
+레드 블랙 트리란 Balanced Binary-Search Tree로, 모든 노드들을 빨간 색 혹은 검은 색으로 칠해 놓았기 때문에 레드-블랙 트리라고 부른다. <br>
+
+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/251fdb6c-11b1-4675-a18f-5f51d406ac7f)
+
+<br>
+
+어이 없지만, 이런 이유로 Red-Black 트리이다. 트리를 처음 고안한 논문의 저자들이 사용할 수 있었던 프린터가 만들어낸 가장 "멋진"색이기 때문이라고 한다. <br> <br>
+
+레드 블랙 트리는, 이런 빨강-검정으로 트리의 노드들을 색칠하고, 색에 대한 규칙을 세워 규칙을 어기는 경우 다시 균형을 맞춰 높이를 낮춘다. <br> 
+균형을 맞추는 트리들이 균형을 맞추는 이유는 트리 Depth를 줄여 빠르게 탐색하기 위해서이다! 편향된 트리를 보면 알겠지만, 탐색 시간 복잡도가 O(N)이 된다. <br>
+
+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/5cb52a3d-29a9-4667-a00b-245c46a2fc78)
+
+가장 아래에 있는 데이터를 찾는 경우 데이터 전체 갯수만큼 탐색하게 된다. <br>
+
+균형을 맞췄을 때, 최악 탐색 시간 복잡도가 줄어들게 되기 떄문에, 균형을 맞추는 것이다.
+
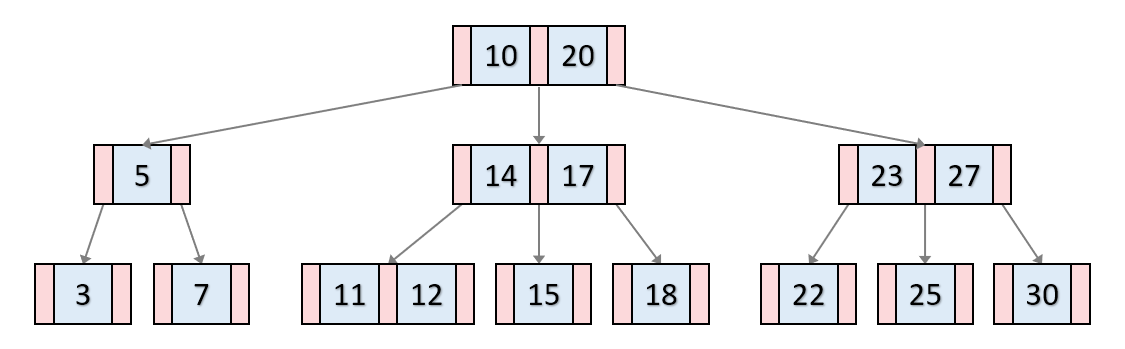+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/afac3f0b-ed2e-4696-b422-633ca215ccd0)
+
+어떤 데이터를 탐색해도 균일하게 빠르다. (시간 복잡도 증명 추가 예정) <br> <br>
+
+
+## 2. Red-Black Tree 규칙
+레드 블랙 트리는 균형을 맞추기 위해 색을 칠한다고 했다. 색칠된 노드들의 규칙을 살펴보자.
+
+1. 모든 노드는 빨강 혹은 검정으로 색칠 되어 있다.
+2. Root는 Black이다.
+3. 모든 Leaf Node는 Black이다.
+4. **빨강 노드는 연속될 수 없다.**
+5. Root 노드에서 모든 Leaf 노드까지 가는 경로의 Black Node 갯수는 같다!
+6. **새로 삽입되는 노드는 빨강이다.** 
+
+<br>
+
+보통 5번까지만 규칙으로 언급되고, 6번은 이해를 용이하기 위해 기재했다. <br> 
+**결국 새로운 노드는 무조건 빨강색으로 삽입되기 때문에, 빨강이 연속되는 순간이 나오게 되는 것이고, 빨강 노드가 연속되는 경우에 균형을 맞추는 작업이 이루어진다.**
+
+
+
+## 3. Red-Black Tree의 균형을 맞추기 위한 연산
+Red-Black Tree가 균형을 맞추는 방식은 2가지이다.
+1. `Recoloring` : 주변 노드들의 색을 변경해 균형을 맞춘다.
+2. `Rotation` : 노드들을 회전 시켜 균형을 맞춘다. AVL Tree처럼 회전시킨다. Restructring이라고 표현하는 한글 아티클도 많은데, 이는 Recolor를 포함하는 표현인듯 하다.
+
+<br>
+
+두 가지 방법을 좀 더 자세히 살펴보자. 그다음 삽입과 삭제시에 무슨 일이 일어나는지 두 가지 방법을 통해 설명하겠다. 그리고 Java 라이브러리의 구현을 살펴보자. 
+
+<br>
+
+### 설명하기 전에..
+1. NIL 노드 : 아무 데이터가 없는 Black 노드이다. Red-Black Tree에서 규칙을 지키기 위해 데이터가 없는 리프 노드를 NIL 노드로 사용한다.
+2. Grand Parent 노드 : 부모의 부모 노드이다.
+3. Parent Sibling 노드 : 말 그대로 부모 노드의 형제 노드이다. Grand Parent Node의 자식 노드 중 부모 노드가 아닌 노드를 이렇게 부르겠다.
+4. 균형은 여러번 맞춰질 수 있다 : 균형을 맞추는 작업을 1회 실시하더라도, 빨간 노드가 연속하는 상황이 벌어질 수 있다. <br> 그런 경우 균형을 맞추는 작업은 여러번 반복된다.
+
+<br>
+
+### 3.1 Recoloring
+
+Recoloring은 말 그대로 노드들의 색을 다시 칠하는 것이다. <br>
+
+![image](https://github.com/binary-ho/Algorithm-and-Data-Structure/assets/71186266/1537a362-0080-4c63-8ad5-aee56ef98e14)
+
+<br>
+
+위 그림에서 파란색 동그라미로 표시한 것이 새 노드이다.
+위 그림처럼 노드들의 색을 바꾸는 것인데, 삽입과 삭제시 색 변경이 다르게 진행될 수 있다.
+
+<br>
+
+### 삽입시 Recoloring
+**Recoloring은 삽입시 부모와, 부모의 형제 노드가 둘 다 빨간색인 경우 발생한다.** <br>
+
+1. 부모 노드와 Parent Sibling 노드를 검은 색으로 변경한다.
+2. 이후 Grand Parent Node를 빨간 색으로 변경한다.
+   - 만약 Grand Parent Node가 루트였다면 검은 색으로 변경한다.
+   - 만약 Grand Parent Node가 빨간색이 되면서, "빨간색 노드는 연속으로 2개가 올 수 없다"규칙이 깨지는 경우, Recoloring 혹은 Rotation을 진행한다.
+
+
+<br>
+
+
+### 3.2 Rotation
+노드들을 회전시킨다. <br>
+AVL Tree의 Rotation을 안다면 그것과 동일하다. <br>
+설명을 너무 복잡하게 하는 곳이 많은데, 그림과 코드를 먼저 보는게 훨씬 쉽다. 코드는 짧지만 상상하면 머리가 복잡해진다. 종이에 직접 그려보면 괜찮다. <br> 
+
+마치 핸들을 돌리듯이 x와 y를 잡고 왼쪽, 오른쪽으로 돌리는 모습을 상상하면 된다!  <br>
+
+
+### Left-Rotate
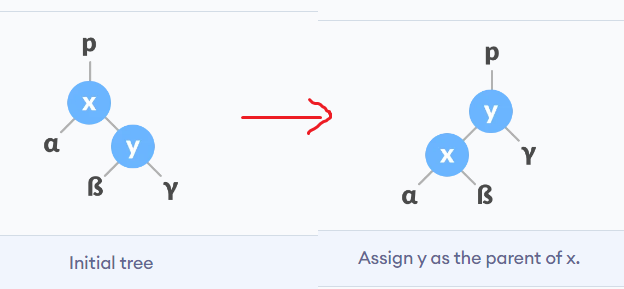+![image](https://github.com/binary-ho/Algorithm-and-Data-Structure/assets/71186266/5faec6e8-5640-4530-9ce5-43e77e583afa)
+
+x, y, 감마를 잡고 왼쪽으로 회전한다고 생각해보면 된다. 위와 같은 상황에서 y에 자식이 있다면, 그 값은 x보다 크고, y보다 작은 것이므로, x의 오른쪽에 가게 된다. 간단한 c++ 코드로는 아래와 같이 구현할 수 있다.
+
+```c++
+x->rightChild = y->leftChild;
+y->leftChild = x;
+```
+
+### Right-Rotate
+
+
+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/ee5b1670-c594-4430-925e-b44650032049)
+
+Left Rotate와 반대이다.
+
+코드로는 아래와 같이 구현할 수 있다 (c++)
+```c++
+y->leftChild = x->rightChild;
+x->rightChild = y;
+```
+
+
+### LR, RL Rotate
+AVL Tree처럼 LR, RL 회전도 있다. 
+
+
+![image](https://github.com/10000-Bagger/free-topic-study/assets/71186266/cd13f4ef-d4a6-4169-aede-b6d1e2015ce3)
+
+LR 회전은 위와 같이 수행되는데, 더 아래에 있는 xy먼저 잡고 Left Rotate를 한 다음, yz를 잡고 Right Rotate한다. 보통 새로 삽입된 노드가 부모의 오른쪽 자식이고, 부모는 Grand Parent Node의 왼쪽 자식일 대 발생한다. <br>
+RL 회전은 반대 상황에서 발생한다.
+
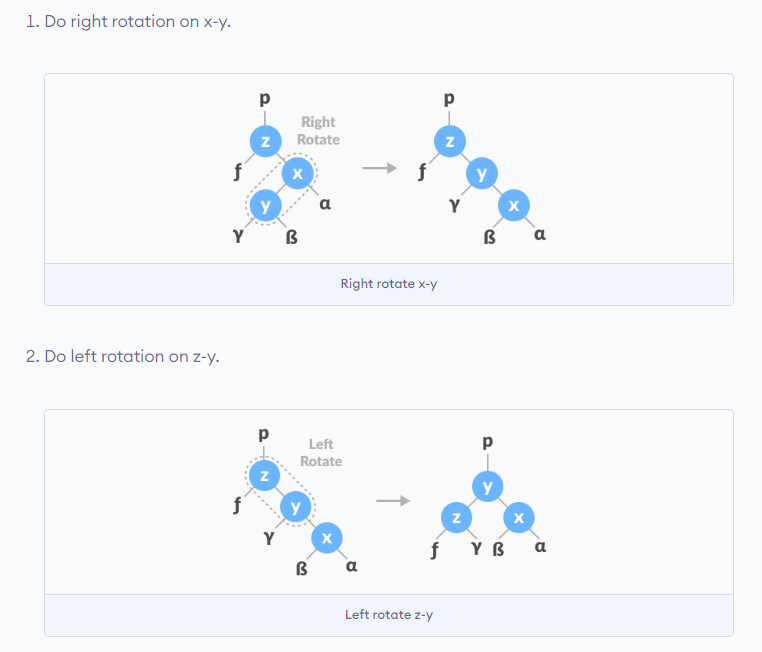+![image](https://github.com/binary-ho/Algorithm-and-Data-Structure/assets/71186266/1ea8e769-d42d-459c-99e0-4fb76d0683f9)
+
+
+<br>
+
+이렇게 균형을 맞추기 위한 연산들을 알아봤다. 이제, 균형을 맞추는 두 연산 `Recolor`와 `Rotate`를 통해  Red-Black Tree의 삽입 연산과 삭제 연산을 알아보자. 그리고 코드를 살펴본 다음, Java 라이브러리에서 어떻게 사용하는지 살펴보자 (HashMap과 TreeSet, TreeMap에서 사용)