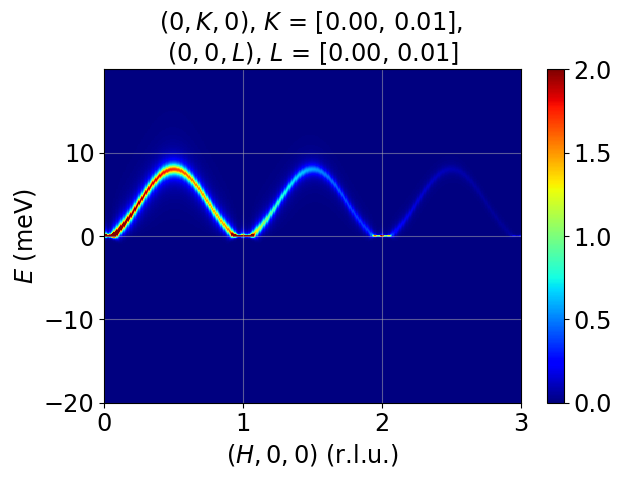
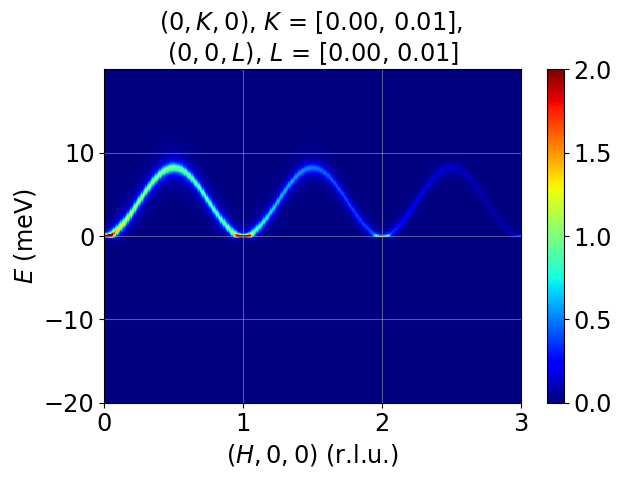
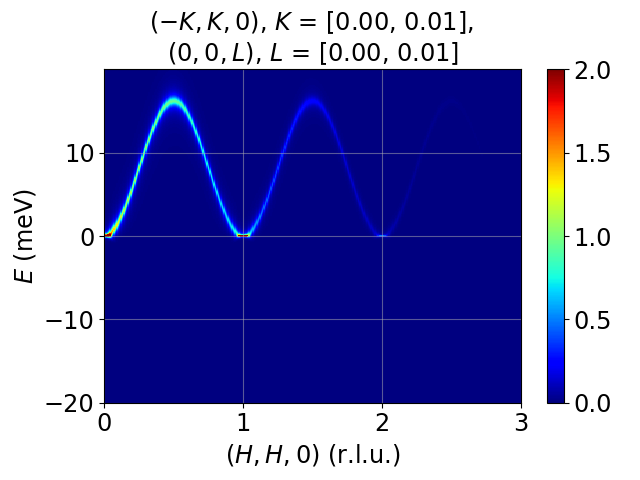
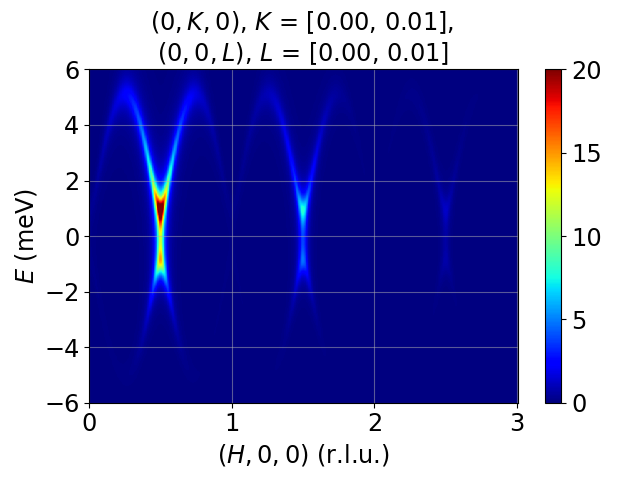
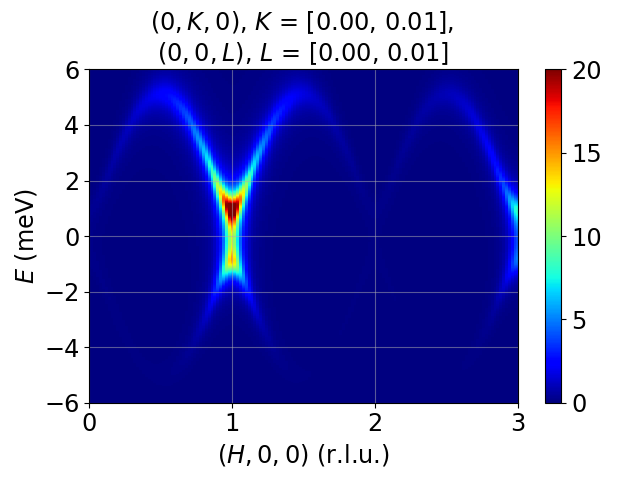
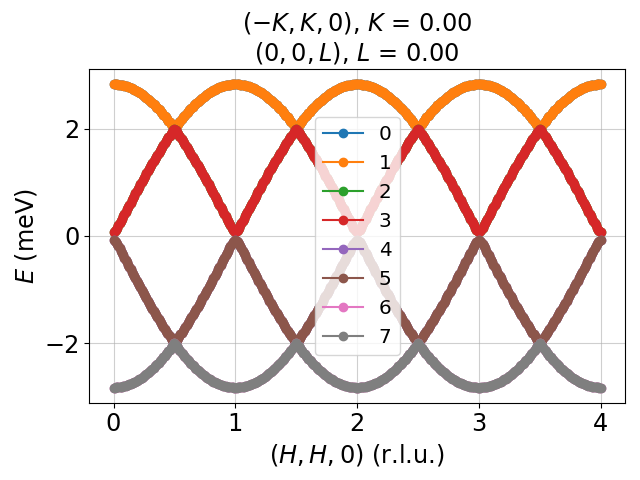
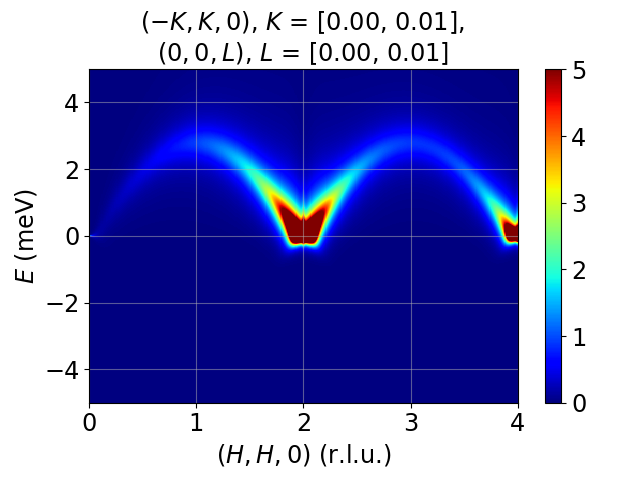
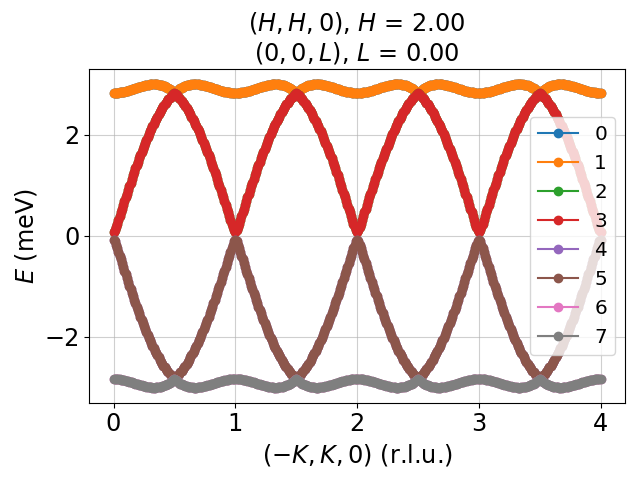
Modeling and simulation of single-crystal spin wave data from inelastic neutron scattering experiments, based on linear spin wave theory, using Python.
Tutorial 1. 1D FM chain
Tutorial 2. 2D FM on a square lattice
Tutorial 3. Neel type AFM chain
Tutorial 4. Neel type AFM chain, modeled using a supercell (Miller indices are doubled)
Tutorial 10. Neel type AFM on a honeycomb lattice, modeled using a supercell (Miller indices are doubled)
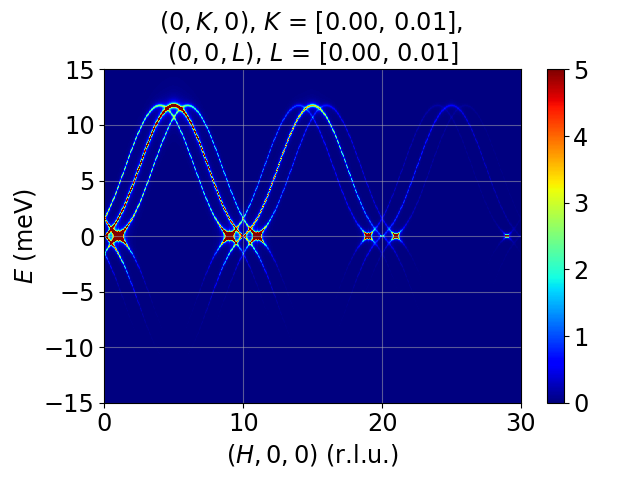
Tutorial 11. 1D incommensurate cycloid chain. Moments rotates in xz-plane, propagation vector tau=(0.1, 0, 0). Cycloid due to competing exchange interation, FM J1 = -1 meV, AFM J2 = 0.309 meV
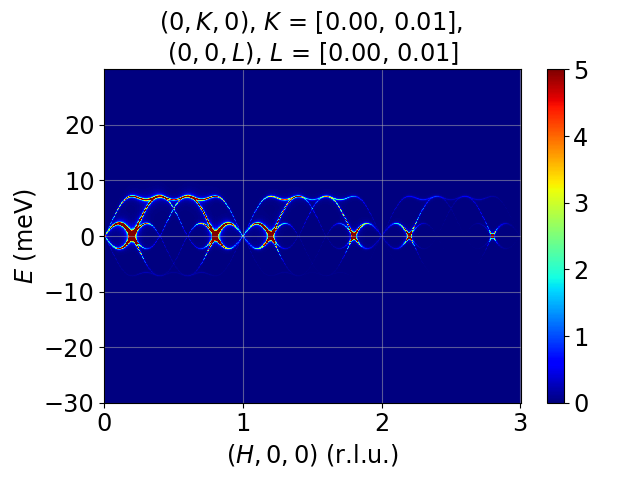
Tutorial 12. 1D incommensurate cycloid chain. Moments rotates in xz-plane, propagation vector tau=(0.1, 0, 0). Cycloid due to competing exchange interation, FM J1 = -1 meV, AFM J2 = 0.309 meV. Calculated using a supercell containing 10 unit cells.
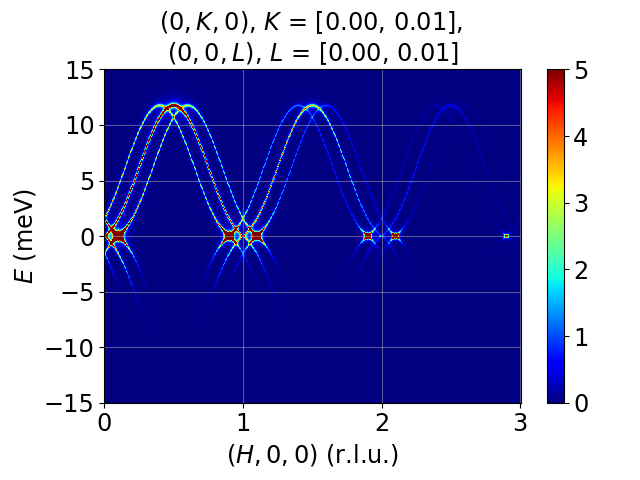
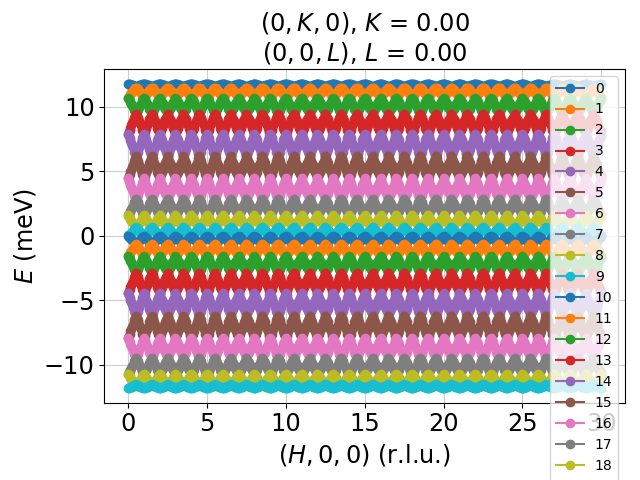
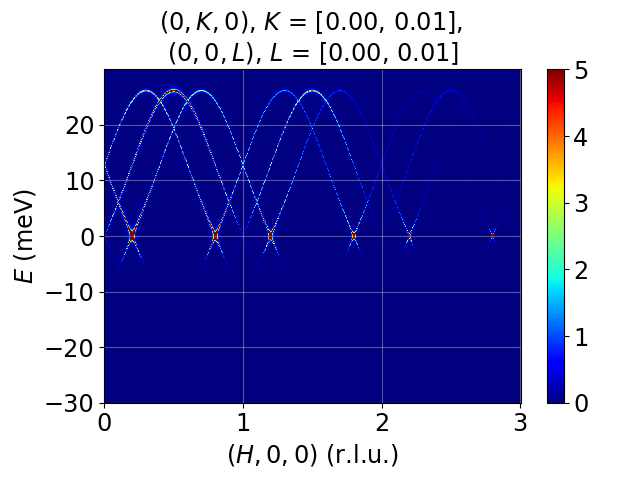
Tutorial 13. 1D incommensurate cycloid chain. Moments rotates in xz-plane, propagation vector tau=(0.1, 0, 0). Cycloid due to DM interation, FM J1 = -1 meV, D_y = +0.727 meV
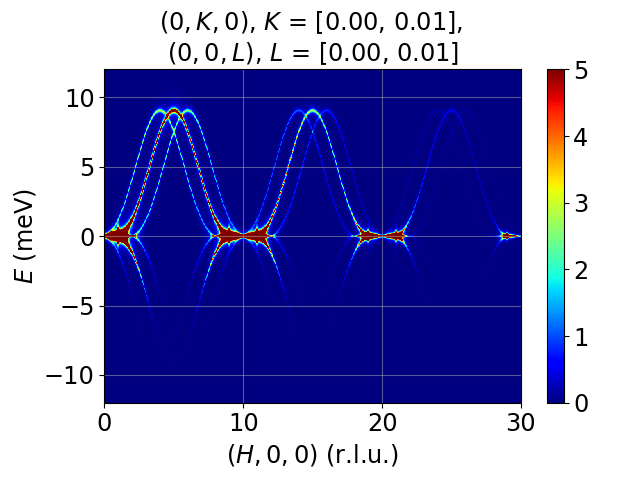
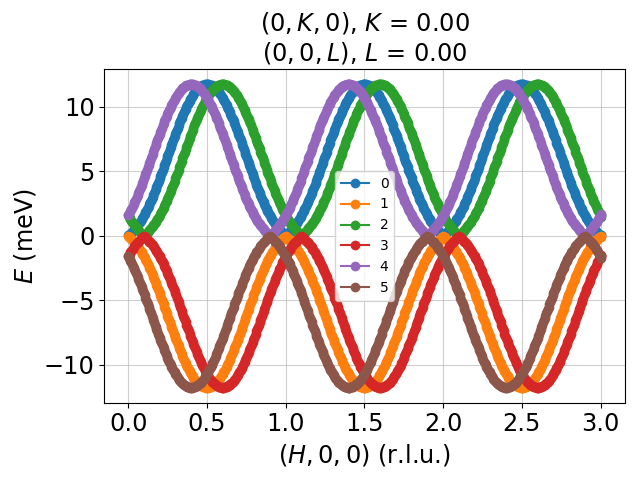
Tutorial 14. 1D incommensurate cycloid chain. Moments rotates in xz-plane, propagation vector tau=(0.1, 0, 0). Cycloid due to DM interation, FM J1 = -1 meV, D_y = +0.727 meV. Calculated using a supercell containing 10 unit cells.
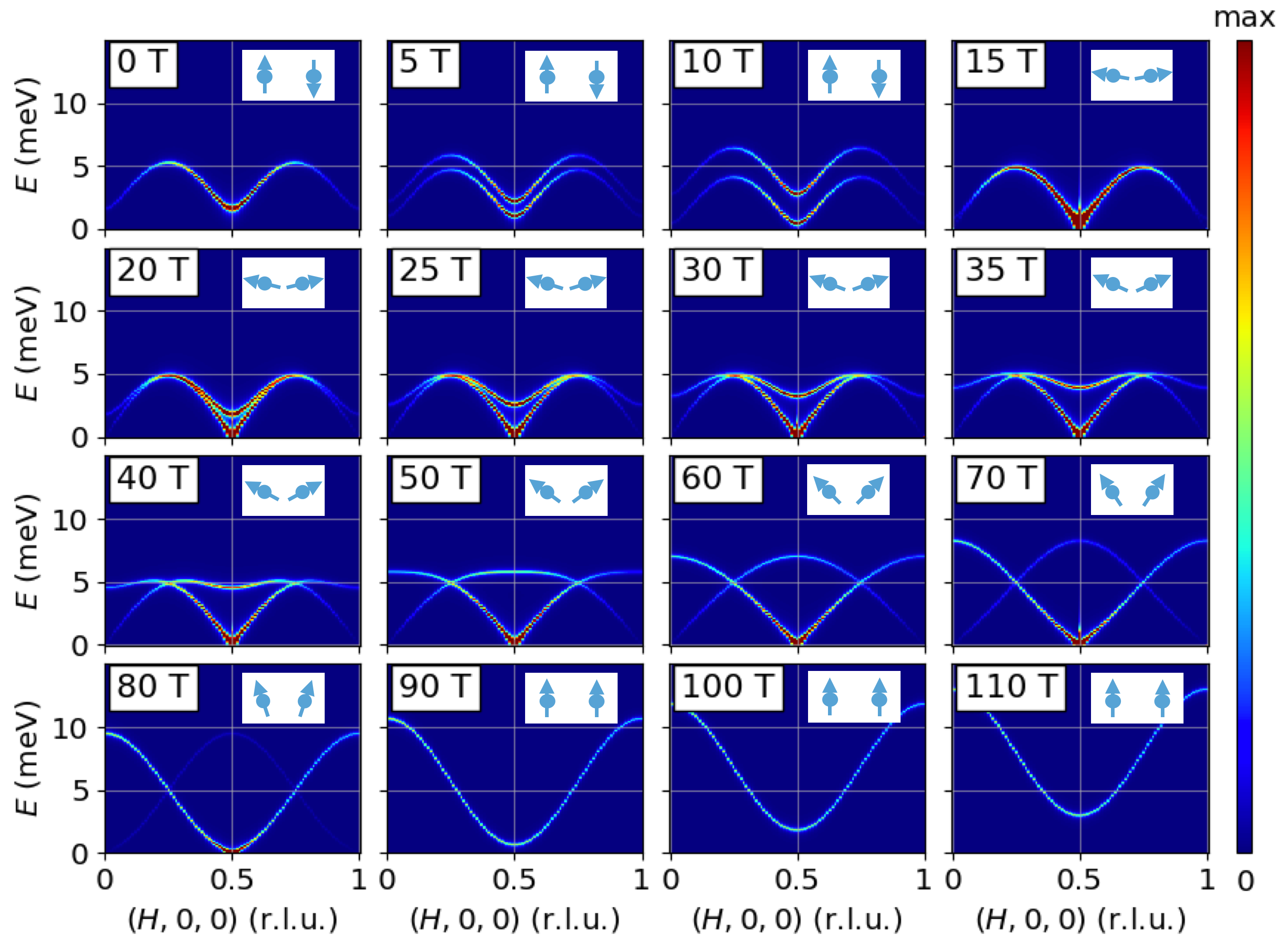
Tutorial 15. Cmoparison of 1D incommensurate cycloid chains due to competeing exchange interactions (CEI) and DM interactions (DMI). Moments rotates in xz-plane, propagation vector tau=(0.2, 0, 0). FM J1 = -1 meV in both cases. In CEI case, AFM J2 = 0.809 meV. In DMI case, Dy = +3.078 meV.
Tutorial 16. 1D Neel AFM chain in applied magnetic field.
