All competitive programming problems have a time limit and a memory limit. Even if your solution is logically 'correct', it may not meet these requirements. Thus, it is important to be able to estimate the runtime and memory usage of your algorithm.
The time complexity of an algorithm gives an estimate of runtime. You can think of it as a rough way of saying how much time you think your code will take to run. It is denoted by O(f(N)) where f(N) is a function of input size N. As input size increases, constant coefficients and lower order terms start to matter less. This is why they are not mentioned in the Big-O notation. For example, if f(N) = 3(N^2) + 2N + 1, complexity is simply O(N^2).
When we say the time complexity of an algorithm is O(f(N)) where N is the size of the input, you can roughly assume that the amount of time the code takes to execute roughly increases as f(N), as the input increases linearly.
If your algorithm does not depend on the size of your input, it will perform in constant time. Mathematical expressions are common examples.
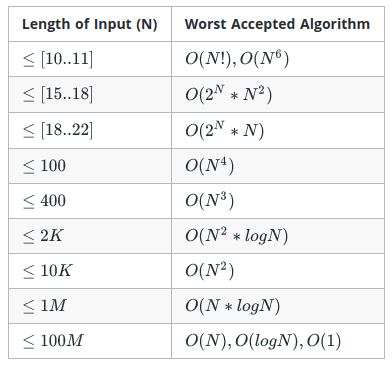
Safe zone: any value of N
This means that as the size of your input increases, the runtime of your algorithm also increases at the same rate, i.e, linearly. If your input is an array, then there is a constant number of operations performed on each of its N elements.
Safe zone: N <= 1e7 (10^7) will run in 1 second.
Quadratic Time Complexity represents an algorithm whose performance is directly proportional to the squared size of the input data set. Within our programs, this time complexity will occur whenever we nest over multiple iterations within the data sets.
Safe zone: N <= 5000
Similar to quadratic, it is another polynomial time complexity.
Safe zone: N <= 500
You definitely would have heard of Binary search, the most common example of logarithmic time. At each step, the problem is halved. If x operations are performed on input of size N, (2^x = N) => (x = logN) (base 2).
Safe zone: N <= 1e18
Efficient sorting algorithms run in log-linear time. Read up on Merge Sort if you're curious.
Safe zone: N <= 1e6
The runtime of your algorithm increases at an exponential rate. The naive (most) method of finding fibonacci numbers is exponential in time.
Safe zone: N <= 20
Generally algorithms that have this sort of running time are those that look at all permutations of a set of elements as there exist n! permuations for a set of n distinct elements.
Safe zone: N <= 10
Space Complexity of an algorithm is an estimate of the memory usage of an algorithm as a function of its input size. Similar to time complexity, space complexity also uses the Big-O notation. Memory limit on Codeforces is usually 256 MB. This is just sufficient to store 1D arrays or vectors of size 1e7. For 2D arrays it is about 1e3 (1e3*1e3 = 1e6) and so on.
Note that some STL containers require more memory, which may lead to an MLE if you're not careful.