Hidden Markov Model
Is a kind of a Directed Graph Model
The HMM is a generative probabilistic model, in which a sequence of observable X variables is generated by a sequence of internal hidden states Z. The hidden states are not be observed directly. The transitions between hidden states are assumed to have the form of a (first-order) Markov chain. They can be specified by the start probability vector π and a transition probability matrix A. The emission probability of an observable can be any distribution with parameters θ conditioned on the current hidden state. The HMM is completely determined by π, A and θ.
There are three fundamental problems for HMMs:
- Given the model parameters and observed data, estimate the optimal sequence of hidden states.
- Given the model parameters and observed data, calculate the likelihood of the data.
- Given just the observed data, estimate the model parameters.
The first and the second problem can be solved by the dynamic programming algorithms known as the Viterbi algorithm and the Forward-Backward algorithm, respectively. The last one can be solved by an iterative Expectation-Maximization (EM) algorithm, known as the Baum-Welch algorithm.
A hidden Markov model is a Markov chain for which the state is only partially observable.
| Category | Usage | Methematics | Application Field |
|---|---|---|---|
| Supervised Learning, Unsupervised Learning | Sequential Labeling | Markov Chain | NLP |
| Markov models | System state is fully observable | System state is partially observable |
|---|---|---|
| System is autonomous | Markov chain | Hidden Markov model |
| System is controlled | Markov decision process | Partially observable Markov decision process |
A Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.
A Markov chain is a stochastic process with the Markov property.
The term "Markov chain" refers to the sequence of random variables such a process moves through, with the Markov property defining serial dependence only between adjacent periods (as in a "chain").
$P={\begin{bmatrix}0.9&0.075&0.025\0.15&0.8&0.05\0.25&0.25&0.5\end{bmatrix}}.$
The Hidden Markov Model
壇子與小球
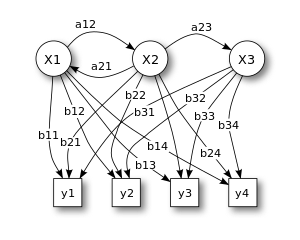
Probabilistic parameters of a hidden Markov model (example)
- X — states
- y — possible observations => only visible thing in HMM!
- a — state transition probabilities
- b — output probabilities
HMM (𝝺) can be defined as (S, V, A, B, 𝞹)
- S: status set
$S = { 1, 2, 3, \dots, N }$
- V: output sign set
$V = {v_1, v_2, \dots, v_M }$
- A: (state) transition matrix (狀態)轉移矩陣
$A_{N\times N} = [a_{ij}]$ $a_{ij} = P(q_t=j|q_{t-1}=i)$
- B: output sign probability distribution
$B = {b_j(k)}$ $b_j(k) = P(v_k|j)$
- 𝞹: initial state probability distribution
$\pi = {\pi_i}$ $\pi_i = P(q_1 = i)$
The hidden markov process can be considered as a double stochastic process:
- the first stochastic process: described with the state transition matrix (can't be observed directly)
- the second stochastic process: defined by the output probability matrix => output the observable signs.
- For a given HMM 𝝺 = (A, B, 𝞹) and an observation sequence O => Calculate observation probability P(O|𝝺)? (i.e. the Probability calculation problem)
- For a given HMM 𝝺 = (A, B, 𝞹) and an observation sequence O => Find the most possible transition sequence q? (i.e. the Prediction problem)
- How to get or update the model's parameter by an observation sequence O? (i.e. the Learning problem)
- based on Maximum Likelihood priniple, how to confirm a set of model parameters that maximize P(O|𝝺)
Example of flipping coin: (this will be used to demonstrate the following problems)
𝝺 = (S, V, A, B, 𝞹)
- S = {1, 2, 3}
- V = {H, T}
- A
A 1 2 3 1 0.90 0.05 0.05 2 0.45 0.10 0.45 3 0.45 0.45 0.1 - B
B 1 2 3 H 0.50 0.75 0.25 T 0.50 0.25 0.75 - 𝞹 = {1/3, 1/3, 1/3}
List all the posibility of the state transition sequence then claculate.
- For the given 𝝺, calculate P(O)
- Calculate P(O, q) (joint probability (聯合機率) of O and q)
- Caculate observation sequence probability P(O)
Time complexity:
- multiply: (2T-1)N^T times
- addition: N^T - 1 times
By the concept of dynamic programming, maybe we can seperate the problem into sub-problem and simplify the problem. => Forward Algorithm, Backward Algorithm
The forward variable
- Initialization (i from 1 to N) $$ \alpha_1(i) = \pi_ib_i(o_1) $$
- Iteration (t from 1 to T-1, j from 1 to N) $$ \alpha_{t+1}(j) = [\sum_{i=1}^N \alpha_t(i) \alpha_{ij}]b_j(o_{t+1}) $$
- Termination $$ P(O|\lambda) = \sum_{i=1}^N \alpha_T(i) $$
Time complexity:
- multiply: N(N+1)(T-1)+N times
- addition: N(N-1)(T-1) times
Calculate the P(HHT|𝝺) of the example:
| H | H | T | |
|---|---|---|---|
| 1 | 0.16667 | 0.15000 | 0.08672 |
| 2 | 0.25000 | 0.05312 | 0.00684 |
| 3 | 0.08333 | 0.03229 | 0.02597 |
P(HHT|𝝺) = 0.11953
The backward variable
- Initialization (i from 1 to N) $$ \beta_1(i) = 1 $$
- Iteration (t from 1 to T-1, j from 1 to N) $$ \beta_{t}(i) = \sum_{i=1}^N \alpha_{ij}b_j(o_{t+1})\beta_{t+1}(j) $$
- Termination $$ P(O|\lambda) = \sum_{i=1}^N \pi_ib_i(o_1)\beta_1(i) $$
The definition of the backward algorithm is not exact symmetric of the forward algorithm. You can define it as a symmetric solution of forward algorithm, but we'll use this algorithm in other problem (the third one)
Calculate the P(HHT|𝝺) of the example:
-
| H | H | T | (initial)
--------|-------|-------|-------|-----------
P(HHT|𝝺) = 0.11953
We can also brute-force to solve this problem. Thus we'll use the DP algorithm again.
It's a variation of forward algorithm
The Viterbi variable
- base case: $$ \delta_1(i) = \pi_ib_i(o_1) $$
- recursive case: $$ \delta_{t+1}(j) = [\max_i\delta_t(i)a_{ij}]b_j(o_{t+1}) $$
- record the path:
$\psi_t(i)$ record the best path from the lastest time (i.e. t-1)
- Initialization (i from 1 to N) $$ \delta_1(i) = \pi_ib_i(o_1) \ \psi_1(i) = 0 $$
- Iteration (t from 1 to T-1, j from 1 to N) $$ \delta_t(j) = \max_i[\delta_{t-1}a_{ij}]b_j(o_t) \ \psi_t(j) = \arg\max_i \delta_{t-1}(i)a_{ij} $$
- Termination $$ P^* = \max{i}\delta_T(i) $$
- Solve the best path $$ q^*_T = \arg\max_i\delta_T(i) $$
Calculate the best state transition sequence of the example:
| H | H | T | |
|---|---|---|---|
| 1 | 0.16667 | 0.07500 | 0.03375 |
| 2 | 0.25000 | 0.02812 | 0.00316 |
| 3 | 0.08333 | 0.02812 | 0.00949 |
| 1 | 0 | 1 | 1 |
| 2 | 0 | 3 | 3 |
| 3 | 0 | 2 | 2 |
so the best state transition sequence is (1, 1, 1)
Principle: Maximum Likelihood Estimation - finds the parameter which maximize P(O|𝝺)
Unknown HMM model 𝝺, given a observation sequence O
- Supervised Learning:
- also give State transition sequence (i.e. the answer)
- pros: easy and good effect
- cons: need the transition sequence, most of the time need manual tagging => high cost
- Unsupervised Learning
- no analytic expression (解析解)
- can only reach local optimal model
Given initial parameters (A, B, 𝞹)
Because we don't have transition sequence. We're not able to calculate state transition frequency, state output frequency and initial state frequency. => Assume all the state transition sequence are possible!
Then calculate the expectation values of them. And update (A, B, 𝞹) with them.
How to pick weight?
For a state transition sequence q, select P(q|O, 𝝺)
But it will only work in theory. We need more efficient algorithm.
In all the possible path, pick
The expectation of the transaction (i,j) occur while time t to t+1
Find the unknown parameters of a hidden Markov model (HMM). It makes use of a forward-backward algorithm.
The variable time t at state i => time t+1 at state j
The variable start from i at time t
Consider all the time
- probability start from state i $$ \sum_{t=1}^{T-1}\gamma_t(i) $$
- probability transit from state i to state j $$ \sum_{t=1}^{T-1}\xi_t(i, j) $$
Then we can estimate (𝞹, A, B)
$$ \bar{a}{ij} = \frac{\sum{t=1}^{T-1}\xi_t(i, j)}{\sum_{t=1}^{T-1}\gamma_t(i)} = \sum_{t=1}^{T-1}\frac{\xi_t(i, j)}{\gamma_t(i)} $$
$$ \bar{b}j(k) = \frac{\sum{t=1}^{T}\gamma_t(j) \times \delta(o_t, v_k)}{\sum_{t=1}^{T}\gamma_t(j)} $$
(
- Initialize (𝞹, A, B) to all 1.
- Iterative calculate new parameter (
$\bar{\pi}, \bar{A}, \bar{B}$ ) - Update them and calculate again...
- Until converge
Baum-Welch Algorithm is a kind of EM algorithm
- E-step:
- Calculate
$\xi_t(i, j)$ and$\gamma_t(i)$ - M-step:
- Estimate model
$\bar{\lambda}$ - Termination condition $$ |\log P(O|\bar{\lambda}) - \log P(O|\lambda)| < \epsilon $$
Floating point overflow problem
- for Forward algorithm
- scaling factors (放大因子) & log
- for Viterbi algorithm
- log
- for Baum–Welch algorithm
- scaling factors