You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
In the proof, I found that after dividing both sides by
we can only conclude that the left part is ≤ 0 (since there is no guarantee that it is ≥ 0 to conclude that it is indeed 0)
I found another approach on Mathematics Stack Exchange which seem to be clearer. The fact that the LHS ≤ 0 for all e_i can still be used to come to conclusion (as we can combine the e_i component to get z in the Stack Exchange proof). But my main point is that we can't conclude LHS = 0
The text was updated successfully, but these errors were encountered:
You can guarantee that the left part is ≥ 0 by redoing the same calculations for $ y - x = - (\epsilon) e_i $. for some small $ \epsilon > 0 $. This was made clear in the exercise session; we will update the solutions to reflect the same.
In the proof, I found that after dividing both sides by
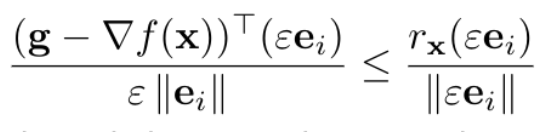
we can only conclude that the left part is ≤ 0 (since there is no guarantee that it is ≥ 0 to conclude that it is indeed 0)
I found another approach on Mathematics Stack Exchange which seem to be clearer. The fact that the LHS ≤ 0 for all e_i can still be used to come to conclusion (as we can combine the e_i component to get z in the Stack Exchange proof). But my main point is that we can't conclude LHS = 0
The text was updated successfully, but these errors were encountered: