Skip to content

Latest commit

 

History

History
228 lines (158 loc) · 26 KB

README.md

File metadata and controls

228 lines (158 loc) · 26 KB
Raw

Predicting the temperature of a superconductor: Regression

By Joe Ganser

ABSTRACT

Data on superconductors was studied with the goal of predicting the critical temperature at which a material undergoes superconductivity; hence a regession task. The data initially consisted of 168 features and 21,263 rows. The goal was not to predict whether or not a material was superconductive, because all data was on superconductive materials. Another researcher had gotten a root mean squared error (RMSE) of ±9.5kelvin on this data set, and this project's goal was to out perform this metric while comparing model techniques and analyzing features. This study was able to get ±9.4Kelvin RMSE. The data is originally sourced from the superconducting material database. This paper is oriented towards an audience of scientists, and was coded in python 3.6.

PROJECT OUTLINE

Introduction

There were several objectives to this project

  • Predict the temperature of superconductivity with the highest possible R2 score and lowest possible RMSE
  • Compare multiple model techniques and find the one that produces the best metrics
  • Identify relevant and irrelevant features
  • Ensure model validity

The approach was to first identify the irrelevant features and discard them, followed by putting the remaining features into a bunch of models for wide comparison.

What is a superconductor?

A superconductor is a material that, at a very, very low temperature allows for infinite conductivity (zero electrical resistance). Essentialy this means thats all the electrons/ions will flow on a material without any disturbance what so ever. One of the most interesting things about superconductors is that at their critical temperature they can create magnetic levitation! This is called the Meissner effect. Lexus, the car company, used this phenomenon to create a hoverboard.

Superconducting temperature

The temperature of at which a material becomes superconductive was what I was trying to predict in this analysis. So why is temperature relevant to super conductivity? To understand this, consider a familiar example of something that's the complete opposite.

A toaster works using electrical resistance. In the circuit of a toaster, the electrons are forced to slow down and colide with each other, which in turn causes an accumulation of thermal energy. That thermal energy then raises the temperature, which cooks the toast.

The physics of a super conductor is (sort of) like the opposite of a toaster. Instead of electrons bumnping into each other chaotically (creating heat), the cold causes them all move uniformly. When the temperature is low enough, the uniform motion of the electrons becomes comes very coherent, producing powerful magnetic fields.

There are many materials that can support superconductivity. Each one is a combination of many different elements, and has many intrinsic properties. Thus by creating a table for each super conductor's properties, along with it's critical temperature, a regression analysis can be done.

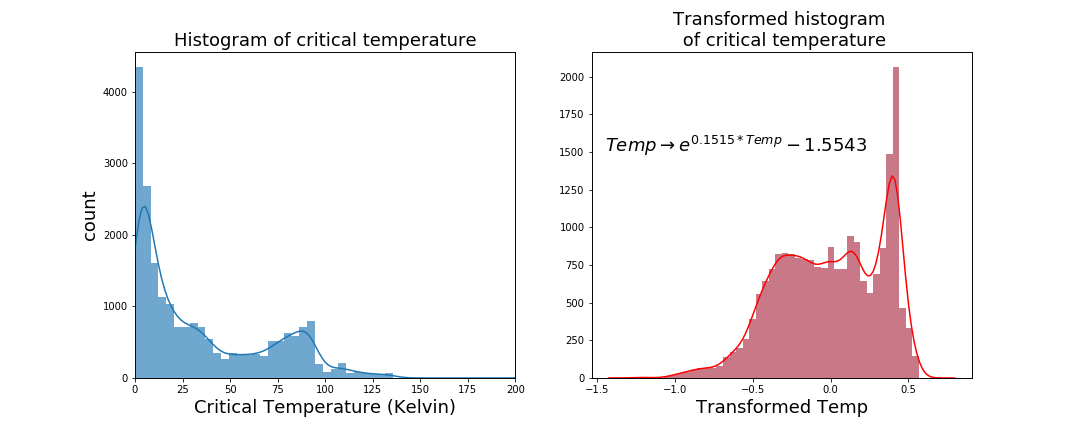
Preprocessing the target variable: critical temperature

In any regression problem, you want the target variable to be as close to a normal distribution as possible. Sometimes this is possible to do, other times not. In this case I was able to transform the critical temperature to be approximately normal.

Originally the data was very, very positively skewed. After a lot of trial and error, I used an exponential transformation to get the data (approximately) normal.

Unfortunately in the best fit there remained a slight skew. The highest peak wasn't simply an outlier and couldn't be dropped or imputed. Despite this, the results observed at the end were pretty good.

Filtering out irrelevant features

Initially the data shape was 21263 rows by 168 features. The head of the original dataframe looked like this;

number_of_elements mean_atomic_mass wtd_mean_atomic_mass gmean_atomic_mass wtd_gmean_atomic_mass entropy_atomic_mass wtd_entropy_atomic_mass range_atomic_mass wtd_range_atomic_mass std_atomic_mass wtd_std_atomic_mass mean_fie wtd_mean_fie gmean_fie wtd_gmean_fie entropy_fie wtd_entropy_fie range_fie wtd_range_fie std_fie wtd_std_fie mean_atomic_radius wtd_mean_atomic_radius gmean_atomic_radius wtd_gmean_atomic_radius entropy_atomic_radius wtd_entropy_atomic_radius range_atomic_radius wtd_range_atomic_radius std_atomic_radius wtd_std_atomic_radius mean_Density wtd_mean_Density gmean_Density wtd_gmean_Density entropy_Density wtd_entropy_Density range_Density wtd_range_Density std_Density wtd_std_Density mean_ElectronAffinity wtd_mean_ElectronAffinity gmean_ElectronAffinity wtd_gmean_ElectronAffinity entropy_ElectronAffinity wtd_entropy_ElectronAffinity range_ElectronAffinity wtd_range_ElectronAffinity std_ElectronAffinity wtd_std_ElectronAffinity mean_FusionHeat wtd_mean_FusionHeat gmean_FusionHeat wtd_gmean_FusionHeat entropy_FusionHeat wtd_entropy_FusionHeat range_FusionHeat wtd_range_FusionHeat std_FusionHeat wtd_std_FusionHeat mean_ThermalConductivity wtd_mean_ThermalConductivity gmean_ThermalConductivity wtd_gmean_ThermalConductivity entropy_ThermalConductivity wtd_entropy_ThermalConductivity range_ThermalConductivity wtd_range_ThermalConductivity std_ThermalConductivity wtd_std_ThermalConductivity mean_Valence wtd_mean_Valence gmean_Valence wtd_gmean_Valence entropy_Valence wtd_entropy_Valence range_Valence wtd_range_Valence std_Valence wtd_std_Valence critical_temp H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe Cs Ba La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn
4 88.9444675 57.862692285714296 66.36159243157189 36.1166119053847 1.1817952393305 1.06239554519617 122.90607 31.7949208571429 51.968827786103404 53.6225345301219 775.425 1010.26857142857 718.1528999521299 938.016780052204 1.30596703599158 0.791487788469155 810.6 735.9857142857139 323.811807806633 355.562966713294 160.25 105.514285714286 136.126003095455 84.528422716633 1.2592439721428899 1.2070399870146102 205 42.914285714285704 75.23754049674942 69.2355694829807 4654.35725 2961.5022857142894 724.953210852388 53.5438109235142 1.03312880053102 0.814598190091683 8958.571 1579.58342857143 3306.1628967555 3572.5966237083794 81.8375 111.72714285714301 60.1231785550982 99.4146820543113 1.15968659338134 0.7873816907632231 127.05 80.9871428571429 51.4337118896741 42.55839575195 6.9055 3.8468571428571403 3.4794748493632697 1.04098598567486 1.08857534188499 0.994998193254128 12.878 1.7445714285714298 4.599064116752451 4.66691955388659 107.75664499999999 61.0151885714286 7.06248773046785 0.62197948704754 0.308147989812345 0.262848266362233 399.97342000000003 57.12766857142861 168.854243757651 138.51716251123 2.25 2.25714285714286 2.2133638394006403 2.21978342968743 1.36892236074022 1.0662210317362 1 1.08571428571429 0.43301270189221897 0.43705881545081 29.0 0.0 0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.2 1.8 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0
5 92.729214 58.518416142857106 73.13278722250651 36.3966020291995 1.44930919335685 1.05775512271911 122.90607 36.161939000000004 47.094633170313394 53.9798696513451 766.44 1010.61285714286 720.605510513725 938.745412527433 1.5441445432697298 0.8070782149387309 810.6 743.164285714286 290.183029138508 354.963511171592 161.2 104.971428571429 141.465214777999 84.3701669575628 1.50832754035259 1.2041147982326001 205 50.571428571428605 67.321319060161 68.0088169554027 5821.4858 3021.01657142857 1237.09508033858 54.0957182556368 1.3144421846210501 0.9148021770663429 10488.571000000002 1667.3834285714302 3767.4031757706202 3632.64918471043 90.89 112.316428571429 69.8333146094209 101.166397739874 1.42799655342352 0.83866646563365 127.05 81.2078571428572 49.438167441765096 41.6676207979191 7.7844 3.7968571428571405 4.40379049753476 1.0352511158281401 1.37497728009085 1.07309384625263 12.878 1.59571428571429 4.473362654648071 4.60300005985449 172.20531599999998 61.37233142857139 16.0642278788044 0.6197346323305469 0.847404163195705 0.5677061078766371 429.97342000000003 51.4133828571429 198.554600255545 139.630922368904 2.0 2.25714285714286 1.8881750225898 2.2106794087065498 1.55711309805765 1.04722136819323 2 1.12857142857143 0.6324555320336761 0.468606270481621 26.0 0.0 0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.9 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.1 1.9 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0
4 88.9444675 57.885241857142894 66.36159243157189 36.1225090359592 1.1817952393305 0.9759804641654979 122.90607 35.741099 51.968827786103404 53.65626773209821 775.425 1010.82 718.1528999521299 939.009035665864 1.30596703599158 0.773620193146673 810.6 743.164285714286 323.811807806633 354.804182855034 160.25 104.685714285714 136.126003095455 84.214573243296 1.2592439721428899 1.13254686280436 205 49.31428571428571 75.23754049674942 67.797712320685 4654.35725 2999.15942857143 724.953210852388 53.9740223651659 1.03312880053102 0.760305152674073 8958.571 1667.3834285714302 3306.1628967555 3592.01928133231 81.8375 112.213571428571 60.1231785550982 101.082152388012 1.15968659338134 0.7860067360250121 127.05 81.2078571428572 51.4337118896741 41.63987779712121 6.9055 3.8225714285714303 3.4794748493632697 1.03743942474191 1.08857534188499 0.927479442031317 12.878 1.75714285714286 4.599064116752451 4.64963546519334 107.75664499999999 60.94376 7.06248773046785 0.6190946827042739 0.308147989812345 0.250477444193951 399.97342000000003 57.12766857142861 168.854243757651 138.54061273834998 2.25 2.27142857142857 2.2133638394006403 2.23267852196607 1.36892236074022 1.02917468729772 1 1.11428571428571 0.43301270189221897 0.444696640464954 19.0 0.0 0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.1 1.9 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0
4 88.9444675 57.8739670714286 66.36159243157189 36.1195603503211 1.1817952393305 1.0222908923957 122.90607 33.7680099285714 51.968827786103404 53.63940496787 775.425 1010.54428571429 718.1528999521299 938.512776724546 1.30596703599158 0.7832066603612908 810.6 739.575 323.811807806633 355.18388442194396 160.25 105.1 136.126003095455 84.371352045645 1.2592439721428899 1.17303291789271 205 46.11428571428571 75.23754049674942 68.52166497852029 4654.35725 2980.33085714286 724.953210852388 53.758486291021796 1.03312880053102 0.7888885322214609 8958.571 1623.48342857143 3306.1628967555 3582.3705966440502 81.8375 111.970357142857 60.1231785550982 100.24495020209 1.15968659338134 0.7869004893749151 127.05 81.0975 51.4337118896741 42.1023442240235 6.9055 3.83471428571429 3.4794748493632697 1.0392111922717702 1.08857534188499 0.96403104867923 12.878 1.7445714285714298 4.599064116752451 4.658301352402599 107.75664499999999 60.97947428571429 7.06248773046785 0.6205354084838871 0.308147989812345 0.257045108326848 399.97342000000003 57.12766857142861 168.854243757651 138.528892724768 2.25 2.26428571428571 2.2133638394006403 2.2262216392083 1.36892236074022 1.04883427304761 1 1.1 0.43301270189221897 0.440952123830019 22.0 0.0 0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.15 1.85 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0
4 88.9444675 57.840142714285705 66.36159243157189 36.11071573753821 1.1817952393305 1.12922373013507 122.90607 27.8487427142857 51.968827786103404 53.5887706050743 775.425 1009.7171428571401 718.1528999521299 937.025572960086 1.30596703599158 0.8052296408133571 810.6 728.8071428571429 323.811807806633 356.31928137213 160.25 106.342857142857 136.126003095455 84.8434418389765 1.2592439721428899 1.26119371912948 205 36.514285714285705 75.23754049674942 70.63444843787241 4654.35725 2923.8451428571398 724.953210852388 53.1170285737926 1.03312880053102 0.859810869291435 8958.571 1491.78342857143 3306.1628967555 3552.6686635803203 81.8375 111.24071428571399 60.1231785550982 97.7747186271033 1.15968659338134 0.7873961825201741 127.05 80.76642857142859 51.4337118896741 43.4520592088545 6.9055 3.8711428571428597 3.4794748493632697 1.04454467078021 1.08857534188499 1.04496953590973 12.878 1.7445714285714298 4.599064116752451 4.6840139510763095 107.75664499999999 61.0866171428571 7.06248773046785 0.624877733754845 0.308147989812345 0.272819938850094 399.97342000000003 57.12766857142861 168.854243757651 138.493671473918 2.25 2.24285714285714 2.2133638394006403 2.20696281450132 1.36892236074022 1.0960519179005401 1 1.05714285714286 0.43301270189221897 0.42880945770867496 23.0 0.0 0 0.0 0.0 0.0 0.0 0.0 4.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0.0 0.3 1.7 0.0 0.0 0.0 0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0 0 0

Thus, several steps were taken to eliminate the irrelevant features. Specifically;

  • Dropping features that varied 5% of less across all rows (using VarianceThreshold)
  • Dropping duplicated features (using .transpose().drop_duplicates(keep='first').transpose())
  • Dropping features with a very small correlation with the target variable (less than |+-0.1|)
  • Dropping features that were highly correlated with each other (greater than |+-0.8|)

It was concluded that 132 features out of the original 168 had very little relevance.

The data that remained, which would be used for modelling, had 36 features and 21263 rows.

The head of the cleaned dataframe was;

number_of_elements mean_atomic_mass range_atomic_mass wtd_range_atomic_mass mean_fie wtd_mean_fie wtd_entropy_fie range_fie wtd_range_fie mean_atomic_radius wtd_range_atomic_radius mean_Density range_Density mean_ElectronAffinity wtd_mean_ElectronAffinity range_ElectronAffinity wtd_range_ElectronAffinity mean_FusionHeat range_FusionHeat mean_ThermalConductivity wtd_mean_ThermalConductivity gmean_ThermalConductivity wtd_entropy_ThermalConductivity range_ThermalConductivity range_Valence wtd_range_Valence critical_temp O S Ca Cu Sr Y Ba Tl Bi
4.0 88.9444675 122.90607 31.7949208571429 775.425 1010.26857142857 0.791487788469155 810.6 735.9857142857139 160.25 42.914285714285704 4654.35725 8958.571 81.8375 111.72714285714301 127.05 80.9871428571429 6.9055 12.878 107.75664499999999 61.0151885714286 7.06248773046785 0.262848266362233 399.97342000000003 1.0 1.08571428571429 29.0 4.0 0.0 0.0 1.0 0.0 0.0 0.2 0.0 0.0
5.0 92.729214 122.90607 36.161939000000004 766.44 1010.61285714286 0.8070782149387309 810.6 743.164285714286 161.2 50.571428571428605 5821.4858 10488.571000000002 90.89 112.316428571429 127.05 81.2078571428572 7.7844 12.878 172.20531599999998 61.37233142857139 16.0642278788044 0.5677061078766371 429.97342000000003 2.0 1.12857142857143 26.0 4.0 0.0 0.0 0.9 0.0 0.0 0.1 0.0 0.0
4.0 88.9444675 122.90607 35.741099 775.425 1010.82 0.773620193146673 810.6 743.164285714286 160.25 49.31428571428571 4654.35725 8958.571 81.8375 112.213571428571 127.05 81.2078571428572 6.9055 12.878 107.75664499999999 60.94376 7.06248773046785 0.250477444193951 399.97342000000003 1.0 1.11428571428571 19.0 4.0 0.0 0.0 1.0 0.0 0.0 0.1 0.0 0.0
4.0 88.9444675 122.90607 33.7680099285714 775.425 1010.54428571429 0.7832066603612908 810.6 739.575 160.25 46.11428571428571 4654.35725 8958.571 81.8375 111.970357142857 127.05 81.0975 6.9055 12.878 107.75664499999999 60.97947428571429 7.06248773046785 0.257045108326848 399.97342000000003 1.0 1.1 22.0 4.0 0.0 0.0 1.0 0.0 0.0 0.15 0.0 0.0
4.0 88.9444675 122.90607 27.8487427142857 775.425 1009.7171428571401 0.8052296408133571 810.6 728.8071428571429 160.25 36.514285714285705 4654.35725 8958.571 81.8375 111.24071428571399 127.05 80.76642857142859 6.9055 12.878 107.75664499999999 61.0866171428571 7.06248773046785 0.272819938850094 399.97342000000003 1.0 1.05714285714286 23.0 4.0 0.0 0.0 1.0 0.0 0.0 0.3 0.0 0.0

Selecting the right model

Seven different types of regression were performed on the data, with the intention of simply estimating the performance of each one without tuning hyperparameters. The metrics of evaluation for each one were the R2 score and the root mean squared error (RMSE). I also measured the time required for each model to fit and predict the data. After all the models and metrics were observed, the best performing one was then selected hyperparameter tuning.

  • Ordinary Least Squares
  • Ridge Regression
  • Lasso Regression
  • Elastic Net regression
  • Bayesian Ridge
  • K-nearest neighbors regression
  • Random Forest Regression

The process of evaluating the models was done by a for loop. At each loop, a sequentially increasing number of features from the data was used on all the models. The order of the features fed into the models was based upon the magnitude of correlation each feature had with the critical_temperature. Hence the first feature used was range_ThermalConductivity which had a correlation of 0.687654, and the last feature was mean_fie which had a correlation of 0.102268. The loop passed through all 36 features. The first iteration had the first feature, the second had the first two features, the third had the first three, and so on. Each model was initially fit without tuning hyperparameters.

In code, the structure was;

#get the correlation of each feature with the target variable
corr = pd.DataFrame(data.corr()['critical_temp'])
#get the absolute value of the correlation
corr['abs'] = np.abs(corr['critical_temp'])
#sort the values by their absolute value, in descending order
corr = corr.sort_values(by='abs',ascending=False)

#loop through the rows of the corr dataframe, getting each feature sequentially
for row in corr.index:
    #add more features iteratively & cumulatively, in order of correlation magnitude
    features = list(corr['index'].loc[:row])
    #use all those features up to that point
    X = df[features]
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=10)
    #fit/train the model
    model.fit(X_train,y_train)
    #then do RMSE and R2 scoring

See the links to coded notebooks for actual code

At each iteration the seven models were fit on a 70-30 train test split. The R2 and RMSE were then measured.

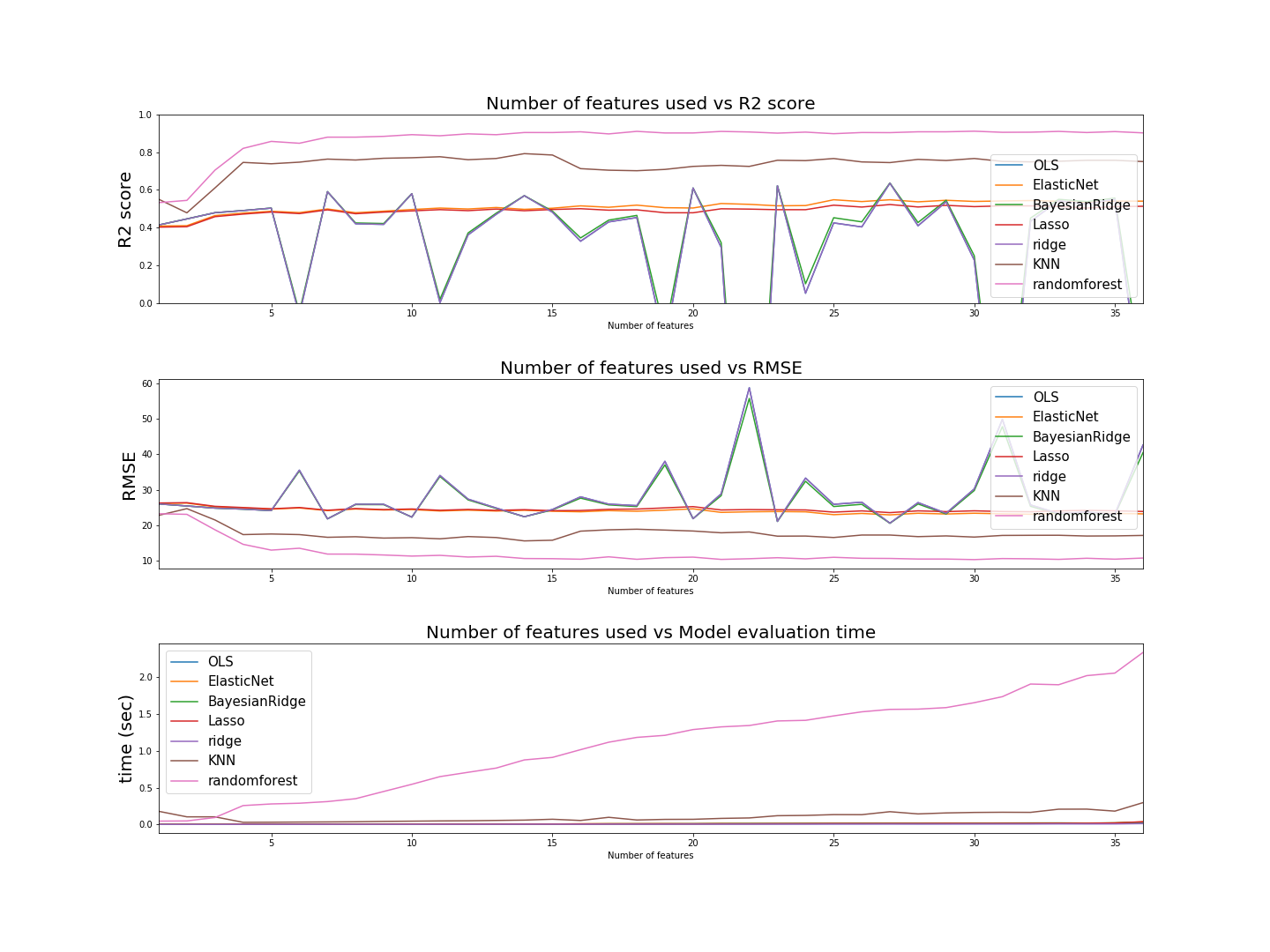
Graphing the evaluation metrics of each model as a function of the number of features used, we have;

The best performance metrics by each model were *(without tuning hyperparameters)*;
model RMSE R2 score # of features used time
RandomForestRegressor 10.3001 0.9104 30 1.6523
KNN 15.5705 0.7917 14 0.0596
BayesianRidge 20.5437 0.6363 27 0.0167
Ridge 20.5642 0.6356 27 0.0061
OLS 20.5645 0.6356 27 0.0123
ElasticNet 22.9051 0.5479 27 0.0153
Lasso 23.5355 0.5227 27 0.0145

Thus, the best performing model (Random Forest regressor) was then fine tuned with it's hyperparameters.

Random Forest: Tuning hyperparameters

Because the main goal is to get the most accurate conclusions about superconductors, accuracy, in this context, is more important than efficiency. Hence, despite random forest regressor being the slowest model to fit the data (over 1 second), it was chosen to be the most important because it had the lowest loss function.

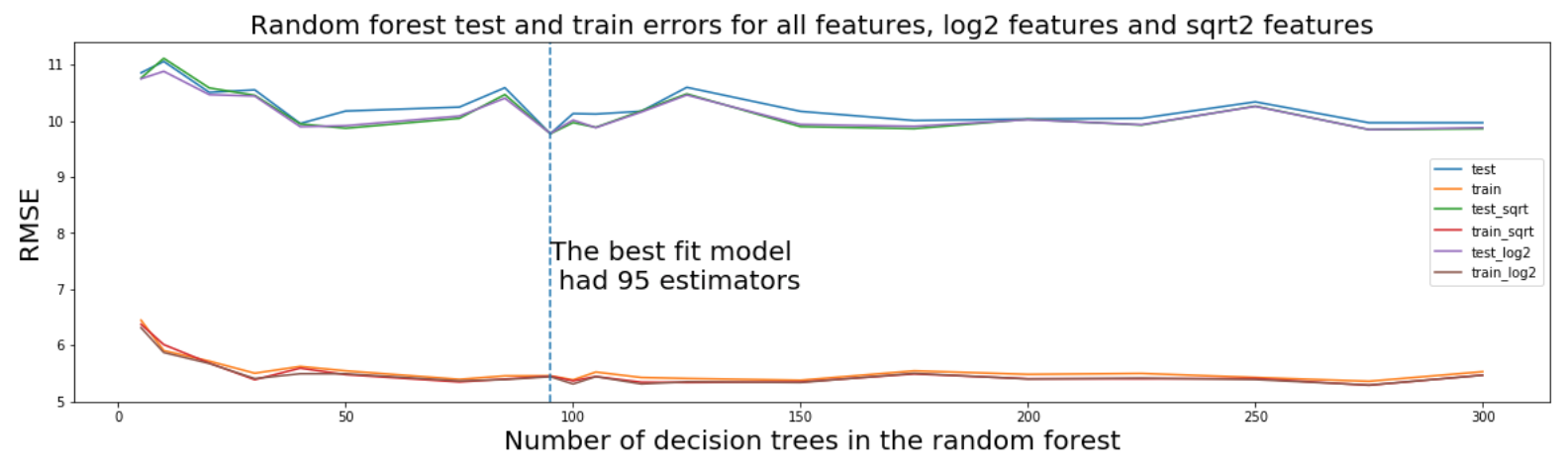
The hyperparameter that was tuned was the number of decision trees in the random forest. To do this,I again used a trial and error approach where I cycled through a range of forest sizes. In conjunction, I also tried using different 'max feature' parameters, specifically log2, sqrt and the default.

After lots of trial and error, a RMSE of ±9.396Kelvin was found, before tuning it was ±10.3Kelvin.

Checking for a good fit

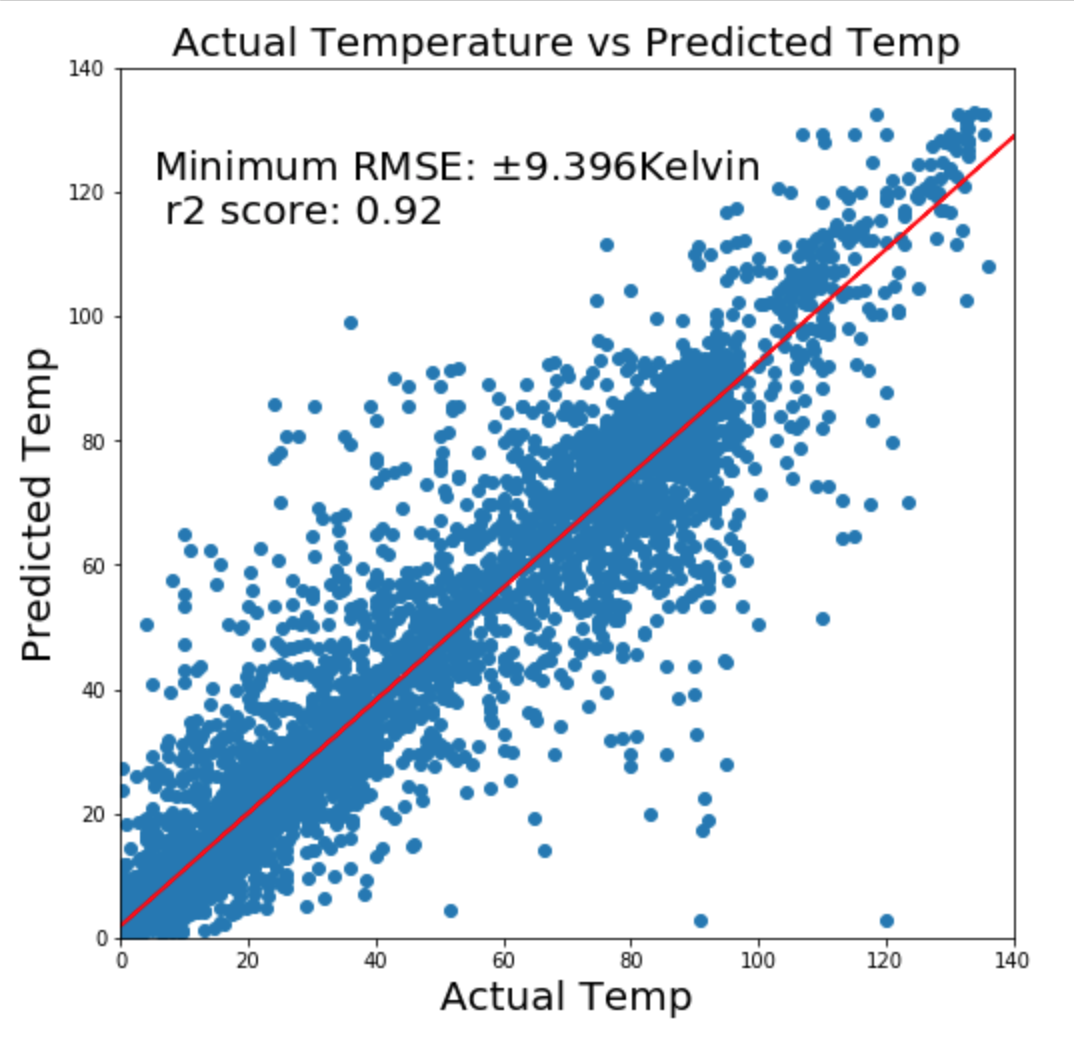
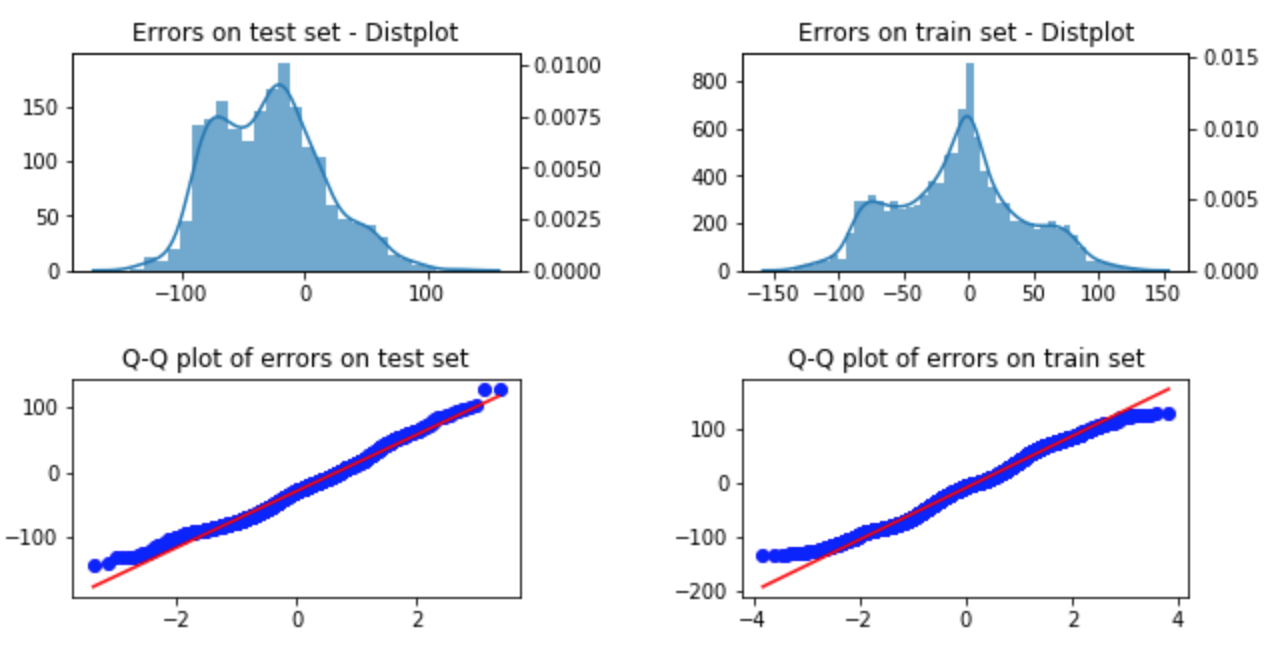
As in any regression analysis, R2 score and RMSE are not the only standards of evaluation. Examining the plot of the predicted values versus actual values is important, as is looking for normality and homoskedascity.

The plot of the predicted temperatures versus actual temperature was

Normality of errors & Homoskedascity

Using seaborn's distplot and probplot functions, I could plot the distribution of errors as well as their Q-Q plots (for both the train sets and the test sets). Approximately normality was observed.

Feature Importance

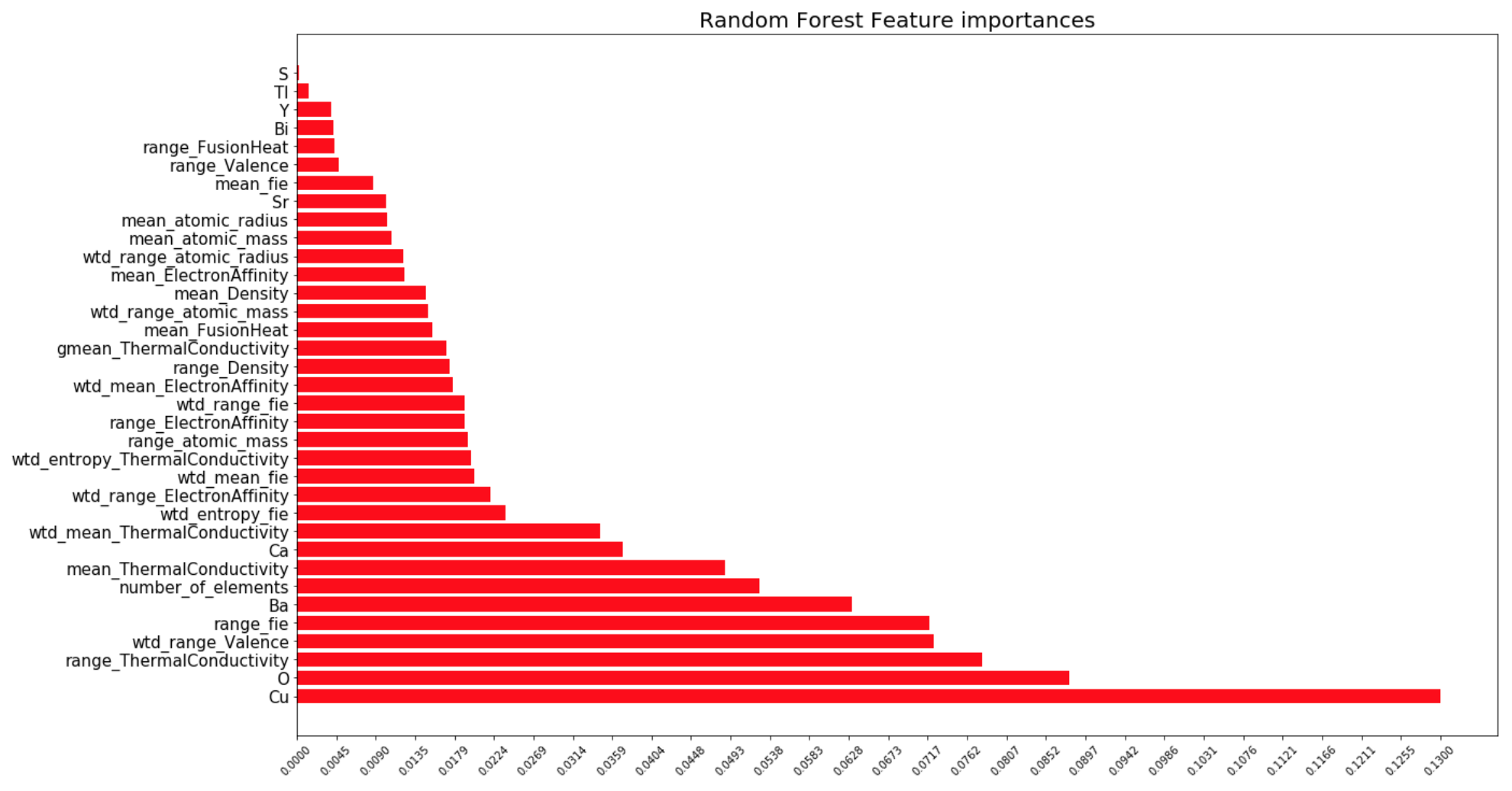
One of the more convenient things about the random forest package is it does feature importance analysis automatically. Here, we can see the relative importances of each measure.

Conclusions

The other researchers that analyzed this data concluded that the important features extracted were ones based on thermal conductivity, atomic radius, valence, electron affinity, and atomic mass. In the graph above we can the same results, with a few extra important features such as the presence of Copper, Oxygen, Barium, the number of elements in the material, et. al. Perhaps it is these few extras I observed that allowed me to get a RMSE of 9.4Kelvin, which is lower than the other research's RMSE of 9.5Kelvin.

Links to coded notebooks

Sources/Links