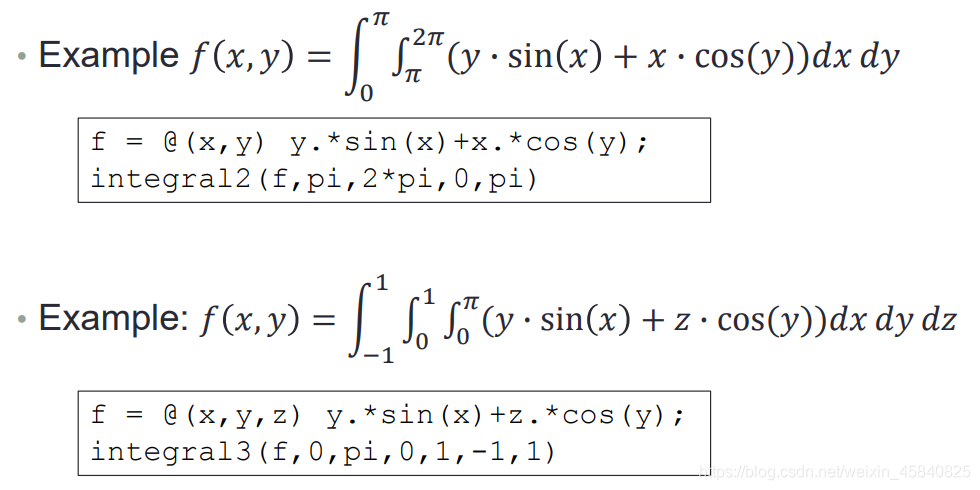Skip to content

Latest commit

 

History

History
117 lines (111 loc) · 7.2 KB

10Integration_&_Differentiation.md

File metadata and controls

117 lines (111 loc) · 7.2 KB
Raw

@TOC

多项式微积分

多项式的值polyval()

y = polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）。 如图，计算多项式在x=-2:0.01:5处的值，并plot()出多项式曲线： [y,delta] = polyval(p,x,S) 使用 polyfit 生成的可选输出结构体 S 来生成误差估计值。delta 是使用 p(x) 预测 x 处的未来观测值时的标准误差估计值。

多项式微分polyder()

k = polyder(p) 返回 p 中的系数表示的多项式的导数； k = polyder(a,b) 返回多项式 a 和 b 的乘积的导数； [q,d] = polyder(a,b) 返回多项式 a 和 b 的商的导数(q为分子，d为分母)。 如图，对多项式求微分，并计算x=7处的微分值：

多项式积分polyint()

q = polyint(p,k) 返回对多项式积分后的多项式系数，常数项为k； q = polyint(p) 常数项 k = 0。 如图，常数项为3，对多项式积分，并计算x=7时的积分值：

数值微积分

数值微分法

diff()

Y = diff(X) 计算相邻元素之间的差分： 如果 X 是长度为 m 的向量，返回长度为 m-1 的向量。Y 的元素是 X 相邻元素之间的差分。Y = [X(2)-X(1) X(3)-X(2) ... X(m)-X(m-1)] 如果 X 是 p×m 矩阵，则返回大小为 (p-1)×m(行变少了) 的矩阵，其元素是 X 的行之间的差分（即每一列中的相邻元素作差分)。Y = [X(2,:)-X(1,:); X(3,:)-X(2,:); ... X(p,:)-X(p-1,:)]

微分法

设置好步长，对x取样x=0:h:2*pi，然后取得各点处函数值f(x)=sin(x)，对x和f(x)分别作差分diff()，再对两者作除法diff(f(x))./diff(x)即可求得该函数各点处的近似微分值。 

h = 0.5; x = 0:h:2*pi;
y = sin(x); 
m = diff(y)./diff(x);
x=0:h:(2*pi-h);
% 因为作差分会缺失最后一个元素，因此x的元素从第1个到end-1
plot(x(1:end-1),m);			%绘制出微分曲线cos(x),

各种步长对比

如下图所示，步长越小，误差越小，微分的曲线与实际曲线越逼近：

较新版本matlab已不再支持symbol，具体解决方案在初阶绘图已有介绍。

高阶微分

高阶微分，在原来的基础上继续微分即可diff(m)./diff(x(1:end-1))，注意x(1:end-1)

数值积分法

获取函数handle

函数的handle可以理解为一个指向该函数的指针，通过@运算符获得； 要想在一个函数A()中调用另一个函数B()，则必须将函数B()的handle作为输入参数传递给函数A()：A(@B,....) 如下图所示，函数xy_plot()可以画出input所指向函数的曲线图，并返回对应的函数值。只需在调用时指定其传入参数即可：

定积分integral()

q = integral(fun,xmin,xmax) 使用全局自适应积分和默认误差容限在 xmin 至 xmax 间以数值形式为函数 fun 求积分。

二、三重积分：

计算广义积分，正/负无穷可以用-Inf/Inf表示



习题

解答该题，可以用conv()函数计算两多项式乘积。 w = conv(u,v) 返回向量 u 和 v 的卷积。如果 u 和 v 是多项式系数的向量，对其卷积与将这两个多项式相乘等效。

clear all;
close all;
x=-2:0.01:1;
a1=[5,-7,5,10]
a2=[4,12,-3];
a=conv(a1,a2);      %计算两多项式相乘所得多项式系数
y=polyval(a,x);
a_=polyder(a);      %计算f(x)微分式的系数
y_=polyval(a_,x);
plot(x,y,'--b',x,y_,'r','linewidth',2);
legend('f(x)','f''(x)');

注意 plot()中设置线条宽度的'linewidth'参数，对前面所画两条线都起作用；添加图例时，在字符串中显示单引号，打两个单引号'f''(x)'即显示一个单引号。 

clear all;
close all;
g=colormap(lines);
hold on;
for i=1:3
    x=0:power(10,-i):2*pi;
    y=exp(-x).*sin(x.^2/2);
    m=diff(y)./diff(x);
    plot(x(1:end-1),m,'Color',g(i,:));
end
hold off;
g=gca;
g.XLim=[0,2*pi]; g.YLim=[-0.3,0.3];
g.FontSize=18;
g.XTick=[0:pi/2:2*pi];
g.XTickLabel={'0','\pi/2','\pi','3\pi/2','2\pi'};
h=legend('h=0.1','h=0.01','h=0.001');



以上内容为个人笔记，部分图片来源于郭老师课件或课程截图。 笔记汇总：MATLAB基础教程 课程视频：https://www.bilibili.com/video/BV1DA411Y7bN 课件下载：MATLAB教程 郭彦甫老师的YouTube主页：@Yanfu Kuo 原视频：https://www.youtube.com/watch?v=KHFZLkm9qs0&t=8s