January 2020
tl;dr: Learn keypoints detection and association at the same time.
This is the foundation of CornerNet which ignited a new wave of anchor less single-stage object detector in 2019.
It can be also used for instance segmentation (and perhaps for tracking as well). Basically any CV problem that can be viewed as joint detection and grouping can benefit from associative embedding.
Super Point learns keypoint detector and embedding at the same time.
The associative embedding idea is also used in Pixels to Graphs.
- Many CV task can be seen as joint detection and grouping (including object detection, as demonstrated by ConerNet later on).
- The output from the network is a detection heatmap and tagging heatmap. The embeddings serve as tags that encode grouping.
- In the detection heatmap, multiple people should have multiple peaks.
- In the tagging heatmap, what matters is not the particular tag values, only the differences between them.
- If a person has m keypoints, the network will output 2*m heatmaps.
- Dimension of embedding: The authors argue that it is not important. If a network can successfully predict high-dimensional embeddings to separate the detections into groups, it should also be able to learn to project those high-dimensional embeddings to lower dimensions, as long as there is enough network capacity.
- Loss: Tags within a person should be the same, and tags across people should be different. Let h be tag value, T = {x_nk} is gt keypoint location
- reference embedding (average embedding of one object): $\bar{h}n = \frac{1}{K} \sum_k h_k (x{nk})$
- pulling force for each person: $L_g(h, T)_{inner} = \frac{1}{N} \sum_n \sum_k (\bar{h}n - h_k(x{n,k}))^2$
- pushing force for different person: $L_g(h, T){outer} = \frac{1}{N^2} \sum_n \sum{n'} exp{-\frac{1}{2\sigma^2} (\bar{h}n - \bar{h}{n'})^2}$
- Inference: max matching by both tag distance and detection score.
-
The system works best if objects are about the same scale. The paper used multiple scales during test time. The heatmaps are averaged, and the embedding are concatenated to a vector. Then compare vectors to determine groups.
-
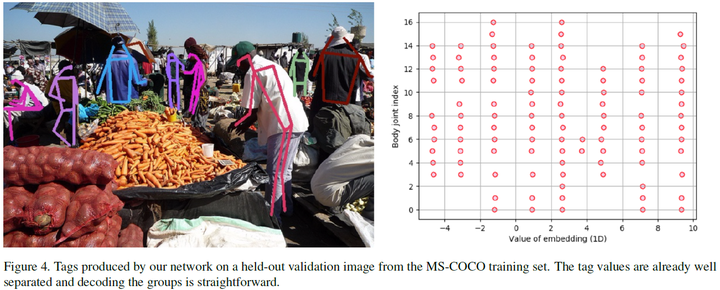
The figure showcasing the 1D embedded results is really cool. This shows the trivial task of grouping after the learning. The clustering is thus trivial. (Otherwise we would need something like mean-shift algorithm to find cluster center first.)
-
The separation between different object in the tagging heatmap is also very impressive.
- Github code in pytorch
- There are other methods for instance embedding such as in the Review of instance embedding