July 2019
tl;dr: Jointly learn an out-of-distribution confidence as "hint".
The intuition is quite thought-provoking and interesting. Give a budget for NN to peak at the label y. If the NN is not sure, it can predict a low conf score so that the label is injected into the prediction. However this is under a budget for predicting low conf.
This idea seems to be easy to implement, and fairly straightforward to generalize to regression tasks. Much easier to understand than Kendall and Yarin's uncertainty paper at NIPS 2017.
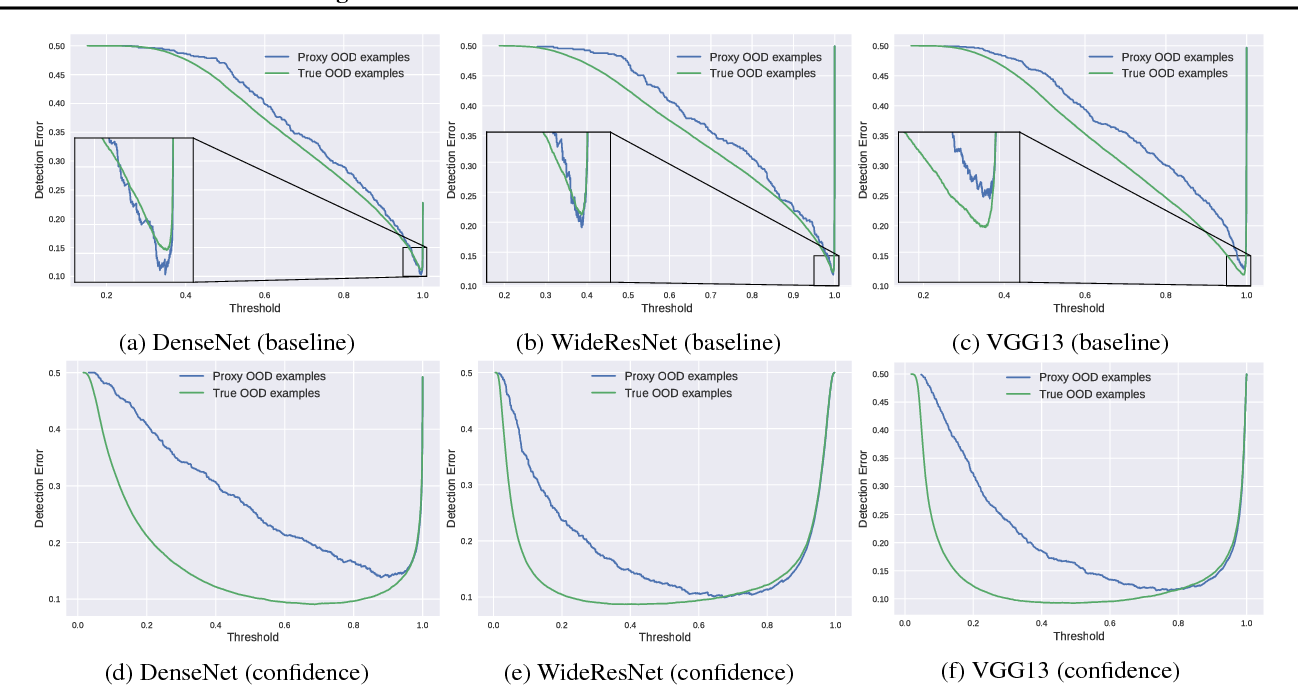
Another benefit of learning this confidence score is that the classifier is less sensitive to threshold in deployment, as evidenced by the flat bottom in Fig. 4.
- Injecting labels to prediction if NN is uncertain about it
$p' = p \cdot c + y \cdot (1-c)$ . - To avoid trivial solution of predicting everything as hard, give a budget, or encouraging to have as many easy case as possible.
$L_c = -\log(c)$ . --> this has been used in numerous other papers to avoid trivial solution, such as the sfm Learner. - Use in-distribution misclassification threshold as proxy for out-of-distribution threshold, if a small out-of-distribution examples are not available.
- Naive implementation will lead to degeneration with conventional scenario where c=1 --> Dynamically adjusting the budget loss weight to encourage NN to use the hint budget.
- Model can lazily opt for free labels instead of learning --> injecting label only to half of the batch
- Overfitting and no misclassified in-class example --> excessive data augmentation
- Eval metrics:
- FPR at 95% TPR
- Detection error
$\min_\delta [0.5 P_{in}(f < \delta) + 0.5 P_{out}(f > \delta)]$ - AUROC
- AUPR