README

一、实验目的

​ 本次作业采用深度学习网络，实现了卷积层、GRU层以及线性全连接层，对Exchange Rate中8个国家7000多条的汇率数据进行训练与。在此基础上，对模型的超参数如CNN、GRU层的深度进行调节，观察不同超参数下模型的效果，尝试找到最优的模型效果。

二、实验数据

2.1 数据介绍

​ Exchange Rate小数据集，包括了8个国家随时间7588条汇率记录。

2.2 数据预处理

​ 在utils.py文件下，封装了DataUtils类，用以数据的读取与处理。

DataUtils._normalized(self, normalize)	# 进行数据的归一化
DataUtils._split(self, train, valid, test) # 切分数据
DataUtils._batchify(self, idx_set, horizon)	# 数据batch化

​ 在主程序中实现DataUtils类，传入数据路径、窗口大小等参数。

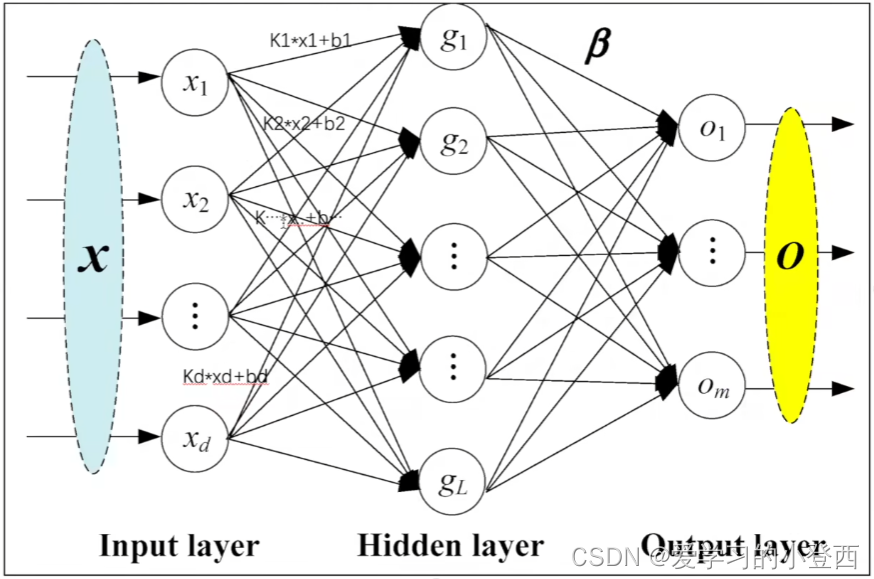
Data = Data_utility(args.data, 0.6, 0.2, args.cuda, args.horizon, args.window, args.normalize)

三、算法实现

​ 本模型总共分为三个部分：卷积层、GRU层、以及线性输出层。如下图所示：

3.1 CNN网络

3.1.1 算法原理

​ 卷积网络 (convolutional network)(LeCun, 1989)，也叫做卷积神经网络 (convolutional neural network, CNN)，是一种专门用来处理具有类似网格结构的数据的神经网络。卷积神经网络主要包括：输入层(Input layer)、卷积层(convolution layer)、激活层（activation layer)、池化层(poling layer)、全连接层(full-connected layer)、输出层(output layer)。卷积具有局部连接、参数共享这两大特征。

3.1.2 算法实现

​ 首先，在模型初始化函数中对卷积层conv1进行初始化，传入相应的模型参数：

class Model(nn.Module):
    def __init__(self, args, data):
        super(Model, self).__init__()
        .......
        # self.hidC：卷积层输出的通道维度
        # self.CK: 卷积核在第一个维度的大小
        # self.m：卷积核在第二个维度的大小
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=self.hidC, kernel_size=(self.Ck, self.m))

​ 其次，在模型先前传播函数forward()中，调用卷积层进行计算，并加入激活层（采用relu）：

def forward(self, x):
   # 转化为卷积层所需的输入维度：tensor(batch_size,168,8) -> tensor(batch_size,1,168,8)
   x = torch.reshape(x, (-1, 1, 168, 8))
   # 卷积后维度变化：tensor(batch_size,1,168,8) -> (batch_size,out_channels,Hout,1)
   # 其中，out_channels、Hout分别与self.hidC、self.Ck参数有关
   x = self.conv1(x)
   x = F.relu(x)
   ...

3.2 GRU层

3.2.1 算法原理

​ 门控循环单元（gated recurrent unit，GRU）是LSTM网络的一种变体，较LSTM网络的结构更加简单，而且效果也不错，因此也是当前非常流行的一种网络。作为LSTM的变体，GRU也可以解决RNN网络中的长依赖问题。

​ 在GRU层中，包括了重置门rt与更新门zt：

• 重置门rt：用于控制前一时刻的隐含层状态有多大程度更新到当前候选隐含层状态；
• 更新门zt：用于控制前一时刻的隐含层状态有多大程度更新到当前隐含层状态。

3.2.2 算法实现

​ 首先，在模型初始化函数中对GRU层进GRU1行初始化，传入相应的模型参数：

class Model(nn.Module):
    def __init__(self, args, data):
        super(Model, self).__init__()
        .......
        # self.hidC：GRU层输入的隐藏层维度大小
        # self.hidR：GRU层输出的隐藏层维度大小
        # batch_first=True：将batch的维度放到第一维
        self.GRU1 = nn.GRU(self.hidC, self.hidR, batch_first=True)
        # dropout层，防止模型过拟合
        self.dropout = nn.Dropout(p=args.dropout)

​ 其次，在模型先前传播函数forward()中，调用卷积层进行计算，并加入Dropout层，防止模型过拟合：

def forward(self, x):
    ...
    # 将最后一个维度去除：tensor(batch_size, out_channels, Hout, 1) -> tensor(batch_size, out_channels, Hout)
    x = x.squeeze(3)
    # 旋转数据的第二、第三维度：tensor(batch_size, out_channels, Hout) -> tensor(batch_size, Hout, out_channels)
    # 其中，Hout作为输入GRU层的序列长度
    x = x.permute(0, 2, 1)
    # GRU1(x)：tensor(batch_size, Hout, out_channels) ->  tensor(1, batch_size, self.hidR)
    x = self.GRU1(x)[1]
    # 对GRU层输出进行dropout，防止过拟合
    x = self.dropout(x)

3.3 Linear层

3.3.1 算法原理

​ 在深度学习中，线性层是神经网络中的一个基本组成部分。它也被称为全连接层或仿射层。线性层主要执行矩阵乘法和加法操作，用于将输入数据转换为输出数据。线性层的输入是一个向量或者一个多维数组（也称为张量），其中每个元素都与神经元的权重相关联。这些权重控制了每个输入元素对输出的贡献程度。线性层会对输入进行加权求和，并加上一个偏置（偏移量）值，然后将结果通过一个非线性激活函数进行处理，产生最终的输出。

3.3.2 算法实现

​ 首先，在模型初始化函数中对线性层进linear1行初始化，传入相应的模型参数：

class Model(nn.Module):
    def __init__(self, args, data):
        super(Model, self).__init__()
        .......
        # self.hidR：GRU层输出的隐藏层维度大小
        # self.m：线性层输出维度，分别表示每个国家的预测结果
		self.linear1 = nn.Linear(self.hidR, self.m)

​ 其次，在模型先前传播函数forward()中，调用线性层进行计算：

def forward(self, x):
    ...
	# linear(x): tensor(1, batch_size, self.hidR) -> tensor(1, batch_size, self.m)
	x = self.linear1(x)

四、实验结果

​ 采用原始参数对模型进行训练，并使用tensorboard进行模型结果进行可视化。在源码中加入：

# 导入tensorboard相关程序包
from torch.utils.tensorboard import SummaryWriter
# 初始化SummaryWriter函数
writer = SummaryWriter('./log_GRU2_CNN1')
# 在每个epoch的训练中，加入下面代码
# 分别存储训练与训练误差
writer.add_scalar(tag='train_loss', scalar_value=train_loss, global_step=epoch)
writer.add_scalar(tag='val_loss', scalar_value=val_loss, global_step=epoch)
writer.add_scalar(tag='val_rae', scalar_value=val_rae, global_step=epoch)
writer.add_scalar(tag='val_corr', scalar_value=val_corr, global_step=epoch)

​ 训练结束后，对结果进行可视化，在相关路径下输入：

tensorboard log=./log

​ 结果与下图所示，经过21-23个epochs的训练之后，模型已经达到饱和。训练误差train_loss不再下降，同时，val_corr相关性也不再上升、测试误差val_loss和c测试集的相对绝对误差val_rae反而呈现了上升的趋势，说明模型出现了过拟合。


​ 

五、超参数调节

5.1 shell脚本实现超参数调节

​ 通过shell脚本调用不同的训练参数进行模型的训练，并保存最优训练结果，从而找出最优的超参数组合。

5.1.1 GPU占用情况查询

​ 在代码运行时，会占用大量的GPU内存。为保证模型在训练时，GPU有充足的资源读取数据、训练模型，我们需要事先对服务器GPU的内存占用情况进行查询。在模型训练的服务器上，有7个Nvidia的GPU，使用shell脚本对其进行占用情况获取。当GPU内存占用情况小于80%，我们便会对其选择该GPU进行训练。否则，我们会挑选其他符合要求的GPU，若均不符合，便等待GPU空闲再进行训练。

#!bin/bash
gpu_list=('1p' '2p' '3p' '4p' '5p' '6p' '7p')
get_gpu(){
  while true;
  do
    for ((i=0; i<=6; i++));
    do
      a=$(nvidia-smi | \
      grep -E "[0-9]+MiB\s*/\s*[0-9]+MiB" | sed -n ${gpu_list[i]} | \
      awk '{print ($9" "$11)}' | \
      sed "s/\([0-9]\{1,\}\)MiB \([0-9]\{1,\}\)MiB/\1 \2/" | \
      awk '{print ($2 - $1)/$2}')
      min=0.8;
      # 若内存空闲>0.8，则使用该颗GPU
      if [ `expr $a \> $min` -eq 0 ];
      then
        continue
      else
        echo $i && return 2
      fi
    done
    sleep 10s
  done
}

5.1.2 各超参数模型训练

​ 使用shell脚本对各种超参数组合进行模型训练，以查找到最优超参数。

# 分别对 batch_size、卷积通道数、RNN输出维度、dropout、GRU层数、学习率进行调节
b_ses=(16 32 64)
hid_CNNs=(30 50 70 90 100)
hid_RNNs=(20 50 70 90 100)
dropouts=(0.3 0.4 0.5 0.6)
GRU_layerses=(1 2 3 4)
lrs=(0.001 0.005 0.01)

for lr in ${lrs[*]};
do
  for hid_CNN in ${hid_CNNs[*]};
  do
    for hid_RNN in ${hid_RNNs[*]};
    do
      for dropout in ${dropouts[*]};
      do
        for b_s in ${b_ses[*]};
          do
            for gru_layers in ${GRU_layerses[*]};
            do
              gpu=$(echo $(get_gpu))
              python main.py --gpu $gpu --data data/exchange_rate.txt --save save/exchange_rate.pt \
              --hidCNN $hid_CNN --hidRNN $hid_RNN \
              --L1Loss False --output_fun None \
              --lr $lr --batch_size $b_s --dropout $dropout --GRU_layers $gru_layers &
              sleep 10s
            done
          done
      done
    done
  done
done

​ 在每组超参数模型训练时，保存其最优的各项数值：

with open(args.save, 'rb') as f:
        model = torch.load(f)
    test_acc, test_rae, test_corr = evaluate(Data, Data.test[0], Data.test[1], model, evaluateL2, evaluateL1,
                                             args.batch_size)
    with open('./search_param.txt', 'a') as f:
        f.write(str(args.batch_size) + '\t' + str(args.hidCNN) + '\t' + str(args.hidRNN) + '\t' \
                + str(args.dropout) + '\t' + str(args.GRU_layers) + '\t' + str(args.lr) + '\t' + str(
            test_acc) + '\t' + str(test_rae) + '\t' + str(test_corr) + '\n')
    print("test rse {:5.4f} | test rae {:5.4f} | test corr {:5.4f}".format(test_acc, test_rae, test_corr))

5.2 超参数调节结果

​ 在完成所有超参数组合的训练后，保留了部分较优的超参数训练组合及其结果，如下表所示。

​ 

​ 我们要找出rse、rae最小以及corr最大的超参数组合。在所有超参数组合中，rse、rae、corr这几个指标最优的超参数组合分别为：

# rse最小的超参数组合
rse=0.075600:{batch_size=32, hidCNN=70, hidRNN=70,dropout=0.3,gru_layers=2,lr=0.001}
# rae最小的超参数组合
rae=0.066900:{batch_size=32, hidCNN=70, hidRNN=70,dropout=0.3,gru_layers=2,lr=0.001}
# corr最大的超参数组合
corr=0.921433:{batch_size=64, hidCNN=100, hidRNN=100,dropout=0.5,gru_layers=1,lr=0.001}

六、总结

6.1 实验总结

​ 在本次实验中，我实现了对LSTNet的搭建，并对模型进行了训练，对训练结果进行了可视化与分析。同时，我使用shell脚本对模型使用不同的超参数组合对模型进行了训练。

​ 算法实现部分详细实现了模型中的三个部分：卷积层、GRU层和线性层。对于卷积层和GRU层，分别说明了它们的原理和实现代码。线性层的原理和实现方法也进行了介绍。在实验结果部分，展示了使用原始参数进行训练的结果，并通过tensorboard对结果进行可视化。通过观察训练误差、验证误差、相关性和相对绝对误差等指标，发现模型出现了过拟合现象。

​ 为找到模型训练的最优超参数，我使用了shell脚本调节训练参数，并通过GPU占用情况查询来优化模型的训练过程。最终我分别找到了在指定范围内模型各指标的最优超参数组合

6.2 思考与展望

​ 在此次实验中，我仅仅实现了对LSTNet较为简单的搭建。其实，可以对LSTNet进行改进以提高模型的表现，如在GRU层加入"Recurrent-skip"层，以捕捉序列模型中的长距离信息；其次，我们还可以在CNN层后加入自回归层，并将其结果加入到最终的预测层中，以提高同一时间节点的信息抓取。

​ 并且，在超参数调节环节，我仅仅遍历各超参数组合进行训练，这样的方法带来了巨大的训练量。虽然我尝试使用7颗GPU同时对不同的超参数组合模型进行训练，但是这仍然会需要较多的训练资源完成超参数的寻找。事实上，我们可以采用现成的最优超参数组合寻找的工具包，这些包大多都设计了对超参数组合的查找策略与算法，如利用Gaussian Process Regression (GPR) 和Tree Parzen Estimator (TPE) 这两种策略进行超参数查找，这些策略会利用已经搜索过的参数的效果，从而减少搜索时间，提高搜索效率。

七、附录

原始形式超参数调节结果

batch_size	hidCNN	hidRNN	dropout	gru_layers	lr	rse	rae	corr
16	30	50	0.4	1	0.0005	0.261	0.2263	0.881619
64	50	50	0.4	1	0.0005	0.1979	0.1759	0.887126
32	50	100	0.4	1	0.0005	0.1431	0.1319	0.901375
16	50	90	0.3	1	0.0005	0.3257	0.3392	0.847092
32	70	100	0.5	1	0.0005	0.119	0.108	0.907325
16	70	70	0.5	1	0.0005	0.119	0.108	0.907325
32	90	100	0.6	1	0.0005	0.1446	0.1316	0.876451
32	100	90	0.5	1	0.0005	0.1446	0.1301	0.912848
64	50	50	0.5	1	0.001	0.1416	0.1357	0.882825
16	30	20	0.3	1	0.001	0.1453	0.123	0.864329
16	30	20	0.3	1	0.001	0.1301	0.1041	0.881731
16	30	20	0.3	1	0.001	0.1816	0.164	0.873879
64	30	20	0.3	1	0.001	0.1296	0.1148	0.867144
32	30	20	0.3	1	0.001	0.3472	0.3246	0.866361
64	30	20	0.4	1	0.001	0.1736	0.1609	0.873311
64	30	20	0.5	4	0.001	0.1594	0.1437	0.871258
64	30	50	0.3	4	0.001	0.3519	0.3064	0.844332
64	30	50	0.4	2	0.001	0.1434	0.1348	0.874478
32	30	50	0.4	1	0.001	0.3059	0.2608	0.884191
64	30	70	0.4	2	0.001	0.1331	0.1333	0.869632
64	30	70	0.3	4	0.001	0.344	0.363	0.854694
16	30	50	0.5	3	0.001	0.312	0.2577	0.860772
32	30	70	0.4	4	0.001	0.1809	0.1543	0.870968
32	30	70	0.5	2	0.001	0.1946	0.1843	0.893729
16	30	70	0.4	1	0.001	0.1521	0.1333	0.843406
16	30	70	0.5	2	0.001	0.1864	0.168	0.890953
64	30	90	0.6	1	0.001	0.1575	0.1518	0.863738
64	30	90	0.5	4	0.001	0.1734	0.148	0.861717
64	30	100	0.3	2	0.001	0.142	0.1277	0.868746
64	30	100	0.3	3	0.001	0.1051	0.1003	0.892627
64	30	100	0.3	4	0.001	0.1269	0.1146	0.918196
32	30	100	0.3	1	0.001	0.3521	0.3142	0.843067
64	30	100	0.5	1	0.001	0.1391	0.1295	0.878264
32	30	100	0.4	3	0.001	0.321	0.2694	0.845897
64	30	100	0.5	2	0.001	0.1017	0.0961	0.867454
32	30	100	0.4	4	0.001	0.1559	0.1486	0.876887
64	30	100	0.6	1	0.001	0.1365	0.1232	0.871811
64	50	20	0.4	2	0.001	0.1788	0.1602	0.870403
32	50	20	0.5	1	0.001	0.2078	0.1953	0.876825
32	50	20	0.5	2	0.001	0.1686	0.1471	0.82298
64	50	20	0.6	1	0.001	0.2284	0.2099	0.888395
64	50	20	0.6	3	0.001	0.3243	0.2971	0.846849
64	50	50	0.4	2	0.001	0.2897	0.2671	0.861934
32	50	50	0.3	3	0.001	0.2913	0.2624	0.872659
64	50	50	0.6	2	0.001	0.2157	0.19	0.891843
16	50	50	0.4	2	0.001	0.1376	0.1203	0.880532
16	50	50	0.3	3	0.001	0.1743	0.1611	0.886062
32	50	50	0.6	3	0.001	0.1936	0.1653	0.902128
64	50	70	0.3	4	0.001	0.2028	0.1776	0.89541
16	50	50	0.4	4	0.001	0.3428	0.3046	0.852823
16	50	50	0.3	4	0.001	0.199	0.1759	0.870343
16	50	50	0.5	3	0.001	0.2916	0.2455	0.858626
64	50	70	0.5	1	0.001	0.165	0.1592	0.877184
16	50	70	0.4	1	0.001	0.2522	0.2255	0.876244
64	50	90	0.3	1	0.001	0.1032	0.0963	0.911591
32	50	70	0.5	4	0.001	0.1743	0.1521	0.890358
64	50	90	0.3	3	0.001	0.3304	0.3001	0.85695
64	50	90	0.4	1	0.001	0.1517	0.1378	0.850876
32	50	90	0.3	3	0.001	0.27	0.238	0.876483
16	50	70	0.4	4	0.001	0.0814	0.0736	0.902559
64	50	90	0.4	4	0.001	0.3049	0.2661	0.845651
32	50	90	0.5	2	0.001	0.0933	0.0875	0.89552
64	50	90	0.6	1	0.001	0.1317	0.1163	0.891612
64	50	90	0.6	4	0.001	0.1733	0.1466	0.883056
64	50	100	0.3	1	0.001	0.1368	0.1264	0.911899
16	50	90	0.5	1	0.001	0.0884	0.0814	0.844725
64	50	100	0.4	3	0.001	0.1366	0.1338	0.903565
64	50	100	0.5	1	0.001	0.1481	0.1307	0.885601
64	50	100	0.5	2	0.001	0.1727	0.1805	0.878763
32	50	100	0.4	3	0.001	0.2378	0.2122	0.892768
64	50	100	0.5	3	0.001	0.1447	0.1381	0.891384
64	50	100	0.5	4	0.001	0.1236	0.1186	0.863299
16	50	100	0.3	3	0.001	0.2677	0.2329	0.875
64	70	20	0.3	2	0.001	0.168	0.1476	0.843544
64	50	100	0.6	4	0.001	0.3937	0.3916	0.841664
32	70	20	0.4	3	0.001	0.1815	0.1697	0.881109
32	70	20	0.6	1	0.001	0.186	0.1648	0.868114
64	70	20	0.6	4	0.001	0.2894	0.2627	0.87688
64	70	50	0.3	1	0.001	0.1604	0.1422	0.877951
32	70	20	0.6	2	0.001	0.2563	0.2396	0.891243
64	70	50	0.3	3	0.001	0.1627	0.147	0.888646
32	70	20	0.5	4	0.001	0.1579	0.146	0.874391
16	70	20	0.5	3	0.001	0.1894	0.1693	0.850064
32	70	50	0.3	3	0.001	0.0938	0.0819	0.852685
16	70	50	0.3	2	0.001	0.2105	0.1908	0.91086
64	70	50	0.6	3	0.001	0.1657	0.1574	0.863438
32	70	70	0.3	2	0.001	0.0756	0.0669	0.838669
64	70	70	0.4	1	0.001	0.2332	0.205	0.904999
32	70	70	0.3	4	0.001	0.3012	0.2776	0.847381
32	70	70	0.4	3	0.001	0.2823	0.2448	0.887182
32	70	70	0.5	1	0.001	0.1336	0.1287	0.902355
16	70	70	0.3	4	0.001	0.1362	0.1191	0.871714
64	70	90	0.3	1	0.001	0.1275	0.1178	0.868062
32	70	90	0.3	1	0.001	0.094	0.0935	0.87467
64	70	90	0.4	1	0.001	0.1682	0.1409	0.861841
64	70	90	0.5	1	0.001	0.1404	0.1229	0.888294
32	70	90	0.4	4	0.001	0.1765	0.1613	0.864548
64	70	100	0.3	1	0.001	0.1324	0.1165	0.917909