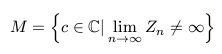fraCtal generates fractals of any dimension that you want. It can generate fractals belonging at two sets: Mandelbrot and Julia.
✅ multithreading support
✅ initial support to custom color palette
✅ color can be personalized
✅ image saved as a PNG file (using lodepng)
🎯 SDL2 support
🎯 ImGUI support
Comparison between 1 vs 4 threads:
| 1-thread | 4-thread | (x0, x1, y0, y1) |
|---|---|---|
| 166.30s | 57.37s | (0.37, 0.40, 0.21, 0.16) |
| 198.322s | 111.56s | (0.37, 0.40, 0.21, 0.26) |
| 46.11s | 21.60s | (2.0, -2.0, 1.7, -1.7) |
You can specify another number of threads in main.c.
There are a lot a change in the color algorithm, and you can change some parameters to make it more or less interesting. A special thanks goes to BrutPitt for the precious hints.
// Blue and red from 0.00 to 255.0
double blue_a = 0.0, blue_b = 255.0;
double red_a = 0.0, red_b = 255.0;
// Fractal must be red on x axis and blue on y axis
double rstepx = (red_b - red_a) / coords->w;
double bstepy = (blue_b - blue_a) / coords->h;The way the green channel get computed is the following:
int val_in = 0, val_out = 0;
int g = 0;
if(k >= 32) {
g = (int)(255.0 - ((((double)k + val_in)) / (coords->max_iterations + val_in) * (255.0-val_out)));
}Below you can see how the fractal looks like:
With val_out = 0 and without attenuation (eg. you can comment the attenuation computation or set it to 1.0):
With:
int val_in = 32, val_out = 150;
int g = 0;
if(k >= 32) {
g = (int)(255.0 - ((((double)k + val_in)) / (coords->max_iterations + val_in) * (255.0-val_out)));
}and without attenuation:
Without attenuation:
int val_in = 32, val_out = 0;
int g = 0;
if(k >= 0) {
g = (int)(255.0 - ((((double)k + val_in)) / (coords->max_iterations + val_in) * (255.0-val_out)));
}With:
double blue_a = 255.0, blue_b = 255.0;
double red_a = 0.0, red_b = 255.0;
int val_in = 32, val_out = 32;
int g = 0;
if(k >= 32) {
g = (int)(255.0 - ((((double)k + val_in)) / (coords->max_iterations + val_in) * (255.0-val_out)));
}
double atten = ((double)k / coords->max_iterations);
atten = 1.0 - (atten*atten);
r = (int)((double)r * atten);
b = (int)((double)b * atten);The image will be:
Last but not least, now is possible load colors (R,G,B) from a text file with the following format:
size (number of lines)
r,g,b
r,g,b
.....
as an example, consider the image on Wikipedia: this are the colors:
16
66,30,15
25,7,26
9,1,47
4,4,73
0,7,100
12,44,138
24,82,177
57, 125,209
134,181,229
211,236,248
241,233,191
248,201,95
255,170,0
204,128,0
153,87,0
106,52,3
you can find it the palette.txt file. As a result we get:
Uncomment PALETTE in mandelbrot.h if you want use them.
On the web there are a lot of explanations about this formula so I don't want to be boring or maybe not totally precise.
Z and C are two complex numbers. Complex numbers are composed by two parts: a real part, and a imaginary part. The formula tell to us that if the value of the function Zn for the value c is not infinite when n approaches infinity, then c belongs to the set. If C belongs to the set, then we choose the black color; otherwise the color will be white.
To determine which will be the color (eg. black or not) we can't obviously iterate to infinity. Luckily maths tell that for definition if the absolute value of Z gets bigger of 2 it will never return closer to 2. So thanks to that we can iterate N times; N could be little but it depends from the number of pixels of the image.
This is my code:
double y = info.y1 + (((double)j * (info.y0-info.y1)) / (double)info.h);
double x = info.x1 + (((double)i * (info.x0-info.x1)) / (double)info.w);Here x and y are the coords of the 2D plan (scaled). In this manner y and x are the imaginary part and the real part of the complex number C seen before (the point that we need to know if belong or not to the set).
The N number is chosen by user. We must just iterate till this value is reached or break the loop if the square root of the abs value is greater then 2; we can simplify this operation removing the sqrt and check for 4.
Here the code:
for(i = 0; i < info.depth; i++)
{
z = complex_sum(complex_mul(z, z), c);
*abs = complex_abs(z);
if(*abs > 4.0) {
break;
}
}Just to summarize: if abs is greater than 4, the C point is not part of the set and it will be left white (but is common give another color based on the amount of iterations); if the value is below 4 then the common color is black because is part of the set.
The area is determined by x0, x1, y0 and y1. They represent the cartesian plane and they are the real part and imaginary part. This four numbers are important because - how we will see - we can use them to zoomin or zoomout in the fractal.
In the first part of this README I had talked about the Zn function and his result that tell to us if the value C belongs to the set or not. When C not belongs to the set we can set a color based on the numbers of the iterations. The intensity of the color differ based on the number of iterations.
If you want to change the primary color (eg, make the fractal red, green or blue or whatever) you must edit the code.
Here some examples; all the images are generated using the same "zoom" (default zooming): x0=2.0, x1=-2.0, y0=2.0, y1=-2.0 and the same iterations, 2.000:
For example, to get this blue, you must use:
int r = iteration>>2;
int g = iteration>>1;
int b = iteration<<3;
r = (r>128) ? 128 : r;
g = (g>128) ? 128 : g;
b = (b>255) ? 255 : b;For the green version, you must change the code in this way:
int r = iteration>>1;
int g = iteration<<3;
int b = iteration>>1;
r = (r>128) ? 128 : r;
g = (g>255) ? 255 : g;
b = (b>128) ? 128 : b;For the red/orange version:
int r = iteration<<2;
int g = iteration>>1;
int b = iteration>>2;
r = (r>255) ? 255 : r;
g = (g>128) ? 128 : g;
b = (b>128) ? 128 : b;Obviously this is not the only way to set a color.
We can also zoom in, how I said before. Let's take a look here, x0=0.37, x1=0.40, y0=0.21, y1=0.26 using the same red color:
How you can see the color make the difference!