- 因为要进行当前位置的有效性判断,所以需要知道当前决策的层数,我使用
track.size()+1表示
使用了一个标志二维数组flag,记录某行某列是否被放置皇后,进而在后面的选择时,可以依据flag进行有效性的判断
bool isvalid(int row, int column) {
// 遍历全部行,检查当前列是否有冲突
for (int i = 1; i < row; i++) {//针对当前列,对row之前的行进行遍历
if (flag[i][column] == 1) {//如果已经选择,不合法
return false;
}
}
//检查左上是否有冲突
for (int i = row - 1, j = column - 1; i >= 1 && j >= 1; i--, j--) {
if (flag[i][j] == 1) {
return false;
}
}
//检查右上是否有冲突
for (int i = row - 1, j = column + 1; i >= 1 && j <= N; i--, j++) {
if (flag[i][j] == 1) {
return false;
}
}
//无冲突
return true;
}因为选择列表是固定的,所以trackback函数参数只有路径,没有选择列表(隐式的存在)
void backtrack(string &track) {
//结束条件:全部皇后都放置完成
if (track.size() == N) {
res.push_back(track);
return;
}
//track.size()<8,皇后未放置完成
int row = track.size() + 1;//对第(track.size+1)行进行选择
for (int i = 1; i <= N; i++) {
int column = i;
//如果当前选择不合法,那么就跳过当次循环
if (!isvalid(row, column)) {
continue;
};
//做选择
track.append(to_string(i));
flag[row][column] = 1;//将此行列设置为1,即皇后放置的位置
backtrack(track);
//撤销选择
track.pop_back();
flag[row][column] = 0;
}
}https://blog.csdn.net/You_are_my_dream/article/details/65631162
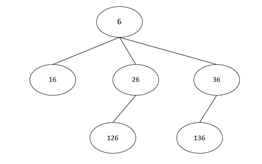
半数集的产生过程可以看做是一个多叉树结构
那么我们使用深度优先搜索将树结构遍历一遍,即可得到半数集中元素的个数
//求n的半数集个数
int dfs(int n) {
//递归出口:半数集只有自身
if (n <= 1) {
return 1;
}
int res = 1;//自己本身肯定在半数集中,那么res初值为1
for (int i = 1; i <= n / 2; ++i) {//可以将半数集看成一个多叉树,这里是遍历多叉树
res += dfs(i);
}
return res;
}典型的回溯问题
给n个不同的正整数集合w和一个正数W,要求找出w的子集,该子集中的所有元素之和为W
- 在将路径加入结果集时,需要判断是否和已有结果集元素重复(或在做选择时排除不合法的选择)
- 因为这是多叉树,那么递归结构需要for循环,来遍历选择列表中的每一个选项;那么
i<可选列表.size(),如果是总路径,会发生段错误
分别写出插入排序与堆排序,每排一个元素就要与中间序列比较一次,如果相同,那么再排一个元素,然后输出即可
分析插入排序与堆排序的区别:
- 插入排序:从前往后有序;当某个元素小于前面的元素,那么它就是下一个待排序元素(依次与前面的元素比较,插入到合适位置);未排序部分与原序列相同
- 堆排序:从后往前有序;当某个元素小于第一个元素,那么表示它还未进行置换,就为下一个待排序元素(将其与首元素交换,然后进行下沉);未排序部分与原序列不同
步骤:
- 检查中间序列的无序部分,若与原序列相同,那么为插入排序,否则为堆排序
- 如果为插入排序,找到待排序元素,即arr1[j]<arr1[j-1]的那个j点
- 如果为堆排序,找到比arr1[0]小的点,即为下一步要进行置换下沉的点
我们先假设这是插入排序,找到arr1[j]<arr1[j-1]的j点,然后比较arr[j,n]与arr1[j,n]是否相同,若相同则为插入排序,否则为堆排序;
- 同样都是并查集问题,社交集群与冰岛家谱有什么区别与联系?
- 使用vector数组来存储当前用户(下标)的父亲节点与母亲节点
- 又分别有sex字符数组和vis整型数组
- 使用dfs进行遍历
将一个整数分解为若干个素数的乘积
判断当前数是否为质数,只需要判断sqrt(n)次即可,因为以此为分界,前后因式一样
定义函数f(int x),作用是将x分解为若干个素数的乘积,并且在开始设置一个质数标志位,如果在[2,sqrt(x)]中没有任何的因子,那么它本省就是一个质数,直接加入进结果集即可
#include <bits/stdc++.h>
double a = 1e3; // a= 1000
double b = 2.3e2; //b = 230
double c = -1.3e2; //c = -130int x;
int main() {
cout << (x = 1) << endl;
cout << &(x = 1) << endl;
cout << &x << endl;
}输出依次是:
1
0x406034
0x406034
可见赋值表达式返回的是表达式左值的引用
说明:在C++编程中,使用set集合时,常用到取并集,交集,差集功能。在算法库中,提供了三个函数可以快速进行这三个操作。
需要包含头文件:
#include <algorithm>基本介绍
set里面有set_intersection(取集合交集)、set_union(取集合并集)、set_difference(取集合差集)、set_symmetric_difference(取集合对称差集)等函数。
其中,关于函数的五个参数问题做一下小结:
特性:这几个函数的前四个参数一样,只有第五个参数有多重版本。
EX1:set_union(A.begin(),A.end(),B.begin(),B.end(),inserter( C1 , C1.begin() ) );前四个参数依次是第一的集合的头尾,第二个集合的头尾。第五个参数的意思是将集合A、B取合集后的结果存入集合C中。
EX2:set_union(A.begin(),A.end(),B.begin(),B.end(),ostream_iterator(cout," “));这里的第五个参数的意思是将A、B取合集后的结果直接输出,(cout," ")双引号里面是输出你想用来间隔集合元素的符号或是空格。
解决不相交集合的合并问题
模板
fa[N]数组:下标表示要进行合并操作的目标元素,拥有的值表示当前元素的祖先元素(也是下标)
元素x的祖先是fa[x],其祖先fa[x]的祖先是其本身,即fa[fa[x]]
并就是对fa数组中的不同集合进行合并,只需将一个集合的祖先指向另一个集合的祖先即可
//查:找到当前元素的祖先
int find(int i) {
//递归出口,当到达祖先位置就返回祖先;否则不断往上查找祖先
return fa[i] == i ? i : fa[i] = find(fa[i]);
}
//并:将a所在集合合并到b所在的集合
void join(int a, int b) {
a = find(a);
b = find(b);
fa[a] = b;//将a的祖先指向b的祖先
}解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯就是在遍历下个节点前,做出选择的操作,遍历之后,再撤销选择
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择核心代码如下:
- 做选择:从选择列表移除,加入路径
- 撤销选择:从路径移除,加入选择列表
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表- 对于排除不合法的选择有两个时机:一是选择前,二是结束条件那里加入结果集时
先写出回溯三要素:
-
路径
一般为数组或字符串,看题目要求
-
选择列表
如果选择列表在决策树的每一层都是固定的,那么可以不显示的声明出来,backtrack函数参数中只写路径即可
-
如果选择列表不固定(例题1)
backtrack函数是
void backtrack(vector<int> track, vector<int> nums){}
for循环是
for (int i = 0; i < nums.size(); ++i) {}
并且每次选择都要移除元素,撤销恢复元素
-
选择列表固定(例题2)
backtrack函数是
void backtrack(string &track){}
for循环是
//N为常数 for (int i = 1; i <= N; i++){}
-
-
结束条件
函数自己调用自己,把当前问题转化为性质相同但是规模更小的子问题
有两个特征:
- 递归出口
- 自我调用
自我调用是在解决子问题,而递归出口定义了最简子问题的答案
比如上面的并查集模板中的find函数:递归出口是定义了最简子问题的答案,自我调用时规模更小但是性质相同
**明白一个函数的作用并相信它能完成这个任务,千万不要试图跳进细节。**千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊
-
遍历二叉树
void traverse(TreeNode* root) { if (root == nullptr) return; traverse(root->left); traverse(root->right); } -
遍历多叉树
使用for循环遍历多叉树,可以参考半数集
void traverse(TreeNode* root) { if (root == nullptr) return; for (child : root->children) traverse(child); }
深度优先搜索与广度优先搜索
-
bfs显式的使用栈,dfs隐式的使用栈(递归)
回溯是dfs的一种
-
bfs
- 将根节点入队
- 将队首节点的全部子节点入队,然后队首出队;如果没有子节点,那么队首直接出队;
- 重复步骤2,直到找到目标元素或队列为空(没找到目标元素)
滑动窗口算法是在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这就降低了问题的复杂度,从而也降低了循环的嵌套深度。滑动窗口主要应用在数组和字符串的场景。
对于类似“请找到满足 xx 的最 x 的区间(子串、子数组)的 xx ”这类问题都可以使用该方法进行解决。
int binarySearch(int arr[], int target) {
int left = 0, right = n - 1;
while (left <= right) {//数组不为空
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {//target在mid右部
left = mid + 1;
} else {//target在mid左部
right = mid - 1;
}
}
return -1;
}//寻找左侧边界的二分查找
int leftBound(int arr[], int target) {
int left = 0, right = n - 1;
while (left <= right) {//数组不为空
int mid = (left + right) / 2;
if (arr[mid] == target) {
right = mid - 1;//因为要找左边界,那么缩小右侧边界,不断向左收缩
} else if (arr[mid] < target) {//target在mid右部
left = mid + 1;
} else {//target在mid左部
right = mid - 1;
}
}
//检查越界
if (left >= n || arr[left] != target)
return -1;
return left;
}//寻找右侧边界的二分查找:在
int rightBound(int arr[], int target) {
int left = 0, right = n - 1;
while (left <= right) {//数组不为空
int mid = (left + right) / 2;
if (arr[mid] == target) {
left = mid + 1;
} else if (arr[mid] < target) {//target在mid右部
left = mid + 1;
} else {//target在mid左部
right = mid - 1;
}
}
//越界检查
if (arr[right] != target || right < 0) {
return -1;
}
return right;//left=right+1
}当使用暴力解法,在连续的空间线性搜索,这就是二分查找可以发挥作用的标志
直接求一个最值很难,但是我们可以很简单的在解空间做判定性问题,比如能不能,行不行,大了还是小了,return true or false,从而缩小解空间(不断的将答案二分),记住,这种方法有个前提条件就是有单调递增或者递减的性质,才能用。这也是binary search使用的条件;
二分搜索:不需要线性搜索,可以快速减小搜索空间(搜索空间每次都减少为原来的一半,复杂度从O(n)->O(logn))
二分搜索除了在有序数组中查找具体值位置,还可以寻找数组中满足条件的第一个/最后一个位置。把序列的元素转化为是否满足条件,转化后是一个[0,0,……1,1,1]的序列,问题转化为求最后一个0/第一个1
核心思想:存在一个分界点(就是我们要求的最值),小于分界点的不合法,大于分界点的合法但是不如它优。那么可以解决一系列最优化问题
- 题目要求最大值或最小值
- 确定答案区间[l,r]
- 判断答案是否单调(小于分界点的合法但是没它优,大于分界点的不合法)
- 确定x是否合法的check函数如何实现
-
给定一个n个点m条边的图,每条边有边权,求从s到t的路径,使得经过的边中边权的最大值最小。
- 题目为求边权的最小值
- 最小值取值范围为取值范围0-边权最大值
- 对于分界点x,如果只用边权<=x的边可以从s到t,那么对于任何x1>x,s依然可以到达t;若x2<x,则s不能到达t
- 合法性的判断函数check(),只保留边权<=x的边,判断s能否到达t(使用并查集或dfs)
-
给定一个有序序列,求大于x的第一个位置(求大于x的最小值)
数组: [1, 2, 5, 7, 13, 15] 查找6 返回4(数组下标1-based)
- 在此例子中7就是分界点,小于7的不合法,大于7的合法但是没它优
-
求给定字符串的最长重复子串中
- 求最长重复子串的长度
- 最大值ans的取值范围为0-size-1
- 对于分界点ans,当子串长度<=ans时,合法但没ans优;当子串长度>ans时,不合法
- 判断函数check()保留长度>ans的值是否合法
二叉树在使用链式存储时,每一个结点都有两个指针,或者为空或者指向子结点。
二叉树所有空指针的个数为n+1(n为二叉树结点个数)
按位取反“~”:按位取反1变0,0变1
逻辑非“!”:逻辑取反, false变true,true变false,在C中,只要不是0就是真
举个例子:
5=000...000101;
5=111...111010;
只要把5前面的连续1都变成0就可以得到最终结果了.那么怎么把前面的1全变成0呢?
首先,确定5的二进制的位数,为3位,即101,我们将1左移3位,得到000...001000;再把这个数减去1,也就得到了000...000111.
用000...000111与5做&运算,不就保留了5最后面的几位,同时把前面的连续1全变成了0了嘛!
int main() {
int n;
cin >> n;
//确定n的二进制位个数为num
int temp = n;
int num = 0;
while (temp > 0) {
temp = temp >> 1;
num++;
}
cout << ((~n) & ((1 << num) - 1));
}工具-编译选项-代码生成/优化-连接器-产生调试信息(yes)