-
Notifications
You must be signed in to change notification settings - Fork 5
Lagrange1d
This document describes a way to optimize a 1D Lagrange code from Gysela. The original code was written for Intel Xeon Phi, so many of the original optimizations decrease performance on other platforms.
// [gys_gl@helios91 proto_lagrange1d]$ export OMP_NUM_THREADS=236; export KMP_PLACE_THREADS=59c,4t; mic_launch
// OK 0 0 0 0, 0.00000e+00 0.00000e+00 0.00000e+00
// OK 25 51 6 3, 5.05127e-01 5.05128e-01 -6.87234e-08
// OK 22 51 6 19, 4.75175e-01 4.75175e-01 -6.46483e-08
// OK 50 102 12 6, -4.13077e-01 -4.13077e-01 5.61999e-08
// OK 47 102 12 22, -4.86272e-01 -4.86272e-01 6.61581e-08
// OK 75 25 19 9, 2.82227e-01 2.82227e-01 -3.83974e-08
// OK 72 25 19 25, 2.13777e-01 2.13777e-01 -2.90847e-08
// OK 97 76 25 28, -5.63214e-01 -5.63214e-01 7.66262e-08
// OK 100 76 25 12, -5.51022e-01 -5.51022e-01 7.49674e-08
// OK 125 127 31 15, -5.86072e-04 -5.86072e-04 7.97361e-11
// OK 122 127 31 31, -1.27696e-03 -1.27696e-03 1.73732e-10
//
// Timer fn_advec lastcall : 2541.00000 us summing up all calls: 37243.00000 us
// == end timer list level 1 ==, lastcalls: 2541.00000 us, summing up : 37243.00000
// Time 2541000.0 nano s, Bandwidth 105.6 GB/s, GFLOps 46.2
//
// [gys_gl@helios88 proto_lagrange1d]$ export OMP_NUM_THREADS=16; unset KMP_PLACE_THREADS; sb_launch
// OK 0 0 0 0, 0.00000e+00 0.00000e+00 0.00000e+00
// OK 50 102 12 6, -4.13077e-01 -4.13077e-01 5.61999e-08
// OK 47 102 12 22, -4.86272e-01 -4.86272e-01 6.61581e-08
// OK 100 76 25 12, -5.51022e-01 -5.51022e-01 7.49674e-08
// OK 97 76 25 28, -5.63214e-01 -5.63214e-01 7.66262e-08
// OK 25 51 6 3, 5.05127e-01 5.05128e-01 -6.87234e-08
// OK 22 51 6 19, 4.75175e-01 4.75175e-01 -6.46483e-08
// OK 72 25 19 25, 2.13777e-01 2.13777e-01 -2.90847e-08
// OK 75 25 19 9, 2.82227e-01 2.82227e-01 -3.83974e-08
// OK 122 127 31 31, -1.27696e-03 -1.27696e-03 1.73732e-10
// OK 125 127 31 15, -5.86072e-04 -5.86072e-04 7.97361e-11
//
// Timer fn_advec lastcall : 4692.00000 us summing up all calls: 28469.00000 us
// == end timer list level 1 ==, lastcalls: 4692.00000 us, summing up : 28469.00000
// Time 4692000.0 nano s, Bandwidth 57.2 GB/s, GFLOps 25.0
//
#ifdef _HANDCLOCK_
#define _CLOCK_VARDEFINE
#include "clock.h"
#endif
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#if defined(__MIC__)
#include <immintrin.h>
#endif
#ifndef NBREPEAT
#define NBREPEAT 2
#endif
#ifndef NR
#define NR 128
#endif
#ifndef NTHETA
#define NTHETA 128
#endif
#ifndef NVPAR
#define NVPAR 32
#endif
#ifndef NPHI
#define NPHI 32
#endif
#define DECNR 8
#define ALLOCSIZER (2*DECNR+NR)
#define FVAL(f,i1,i2,i3,i4) \
f[DECNR+i1+ALLOCSIZER*(i2+NTHETA*(i3+NPHI*(i4)))]
typedef struct {
double thetamin, dtheta;
double phimin, dphi;
double rmin, dr;
double vparmin, dvpar;
double *thetatmp;
double *phitmp;
double *rtmp;
} geom_t;
int fn_init(double *f, geom_t *geom) {
int ivpar, iphi, itheta,ir;
double rval, thval, pval, vval;
geom->rtmp = malloc(NR*sizeof(double));
geom->thetatmp = malloc(NTHETA*sizeof(double));
geom->phitmp = malloc(NPHI*sizeof(double));
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr );
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,rval,thval,pval,vval)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma ivdep
for (ir=0; ir<NR; ir++) {
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
FVAL(f,ir,itheta,iphi,ivpar) = rval * thval * pval * vval;
}
}
}
}
return 0;
}
int fn_verif(double *f, geom_t *geom) {
int ivpar, iphi, itheta, ir;
int64_t count, modulo;
double rval, thval, pval, vval;
double numres, exact;
modulo = NR*NTHETA*NPHI*NVPAR/10;
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr +.5*geom->dr);
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,count,rval,thval,pval,vval, \
numres,exact)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
for (ir=0; ir<NR; ir++) {
count=ir+NR*(itheta+NTHETA*(iphi+NPHI*ivpar));
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
numres = FVAL(f,ir,itheta,iphi,ivpar);
exact = rval * thval * pval * vval;
if (!(fabs(numres-exact) < 1.e-4)) {
#pragma omp critical
{
printf( "ERROR! at %d %d %d %d, %.5e %.5e %.5e\n",
ir,itheta,iphi,ivpar,numres,exact,numres-exact );
exit(2);
}
} else {
if (count%modulo == 0) {
#pragma omp critical
{
printf( "OK %d %d %d %d, %.5e %.5e %.5e\n",
ir,itheta,iphi,ivpar,numres,exact,numres-exact );
}
}
}
}
}
}
}
return 0;
}
inline void lag4(double posx, double *coef) {
double loc[4] = { -1./6., 1./2., -1./2., 1./6. };
coef[0] = loc[0] * (posx-1.) * (posx-2.) * (posx-3.);
coef[1] = loc[1] * (posx) * (posx-2.) * (posx-3.);
coef[2] = loc[2] * (posx) * (posx-1.) * (posx-3.);
coef[3] = loc[3] * (posx) * (posx-1.) * (posx-2.);
}
int fn_advec_int(double *f0, double *f1, geom_t *geom) {
int ivpar, iphi, itheta, ir;
double numres, posx;
double coef0, coef1, coef2, coef3;
#if defined(__MIC__)
__assume_aligned(f0, 64);
__assume_aligned(f1, 64);
TIMER_DEFINE(advec1D, "fn_advec_int" , 1);
TIMER_BEGIN(advec1D);
#pragma omp parallel private(ir,itheta,iphi,ivpar, \
numres,coef0,coef1,coef2,coef3,posx)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
#pragma omp for schedule(static) collapse(2)
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
register __m512d coeff1;
register __m512d coeff2;
register __m512d coeff3;
register __m512d coeff4;
register double* ptread;
register __m512d tmpw;
register __m512d tmpr1;
register __m512d tmpr2;
register __m512d tmpr3;
register __m512d tmpr4;
posx = 1.5;
// 6*4/8=3 flop par indice ir
coeff1 = _mm512_set1_pd(-1./6. * (posx-1.) * (posx-2.) * (posx-3.));
coeff2 = _mm512_set1_pd(1./2. * (posx) * (posx-2.) * (posx-3.));
coeff3 = _mm512_set1_pd(-1./2. * (posx) * (posx-1.) * (posx-3.));
coeff4 = _mm512_set1_pd(1./6. * (posx) * (posx-1.) * (posx-2.));
#pragma vector nontemporal
#pragma vector always
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,ir-DECNR,itheta,iphi,ivpar) = FVAL(f0,NR-DECNR+ir,itheta,iphi,ivpar);
}
#pragma vector nontemporal
#pragma vector always
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,NR+ir,itheta,iphi,ivpar) = FVAL(f0,ir,itheta,iphi,ivpar);
}
#pragma novector
for (ir=0; ir<NR; ir+=8) {
ptread = &(FVAL(f0,ir,itheta,iphi,ivpar));
tmpr2 = _mm512_load_pd (ptread);
tmpr1 = _mm512_loadunpacklo_pd(tmpr1, ptread-1);
tmpr1 = _mm512_loadunpackhi_pd(tmpr1, ptread-1+8);
tmpr3 = _mm512_loadunpacklo_pd(tmpr3, ptread+1);
tmpr3 = _mm512_loadunpackhi_pd(tmpr3, ptread+1+8);
tmpr4 = _mm512_loadunpacklo_pd(tmpr4, ptread+2);
tmpr4 = _mm512_loadunpackhi_pd(tmpr4, ptread+2+8);
// 1+2+2+2=7 flop par indice ir
tmpw = _mm512_mul_pd(tmpr1,coeff1);
tmpw = _mm512_fmadd_pd(tmpr2,coeff2,tmpw);
tmpw = _mm512_fmadd_pd(tmpr3,coeff3,tmpw);
tmpw = _mm512_fmadd_pd(tmpr4,coeff4,tmpw);
_mm512_store_pd (&(FVAL(f1,ir,itheta,iphi,ivpar)), tmpw);
}
}
}
}
TIMER_END(advec1D);
#endif
return 0;
}
int fn_advec_unroll_try(double *f0, double *f1, geom_t *geom) {
int ivpar, iphi, itheta, ir, cir;
double numres, posx, tmpf;
double coef0, coef1, coef2, coef3;
__assume_aligned(f0, 64);
__assume_aligned(f1, 64);
TIMER_DEFINE(advec1D, "fn_advec" , 1);
TIMER_BEGIN(advec1D);
#pragma omp parallel private(ir,itheta,iphi,ivpar,cir, \
numres,coef0,coef1,coef2,coef3,posx,tmpf)
#pragma omp for schedule(static) collapse(3)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,ir-DECNR,itheta,iphi,ivpar) = FVAL(f0,NR-DECNR+ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,NR+ir,itheta,iphi,ivpar) = FVAL(f0,ir,itheta,iphi,ivpar);
}
posx = 1.5;
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<NR; ir++) {
double coeff[] = {-1./6. * (posx-1.) * (posx-2.) * (posx-3.) ,
1./2. * (posx) * (posx-2.) * (posx-3.) ,
-1./2. * (posx) * (posx-1.) * (posx-3.) ,
1./6. * (posx) * (posx-1.) * (posx-2.) };
tmpf = 0;
#pragma unroll(4)
for (cir=0; cir<4; cir++) {
tmpf += FVAL(f0,ir-1+cir,itheta,iphi,ivpar) * coeff[cir];
}
// 7 flop par indice ir
FVAL(f1,ir,itheta,iphi,ivpar) = tmpf;
}
}
}
}
TIMER_END(advec1D);
return 0;
}
int fn_advec(double *f0, double *f1, geom_t *geom) {
int ivpar, iphi, itheta, ir;
double numres, posx;
double coef0, coef1, coef2, coef3;
__assume_aligned(f0, 64);
__assume_aligned(f1, 64);
TIMER_DEFINE(advec1D, "fn_advec" , 1);
TIMER_BEGIN(advec1D);
#pragma omp parallel private(ir,itheta,iphi,ivpar, \
numres,coef0,coef1,coef2,coef3,posx)
#pragma omp for schedule(static) collapse(3)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,ir-DECNR,itheta,iphi,ivpar) = FVAL(f0,NR-DECNR+ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,NR+ir,itheta,iphi,ivpar) = FVAL(f0,ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<NR; ir++) {
posx = 1.5;
FVAL(f1,ir,itheta,iphi,ivpar) =
-1./6. * (posx-1.) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+0,itheta,iphi,ivpar) +
1./2. * (posx) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+1,itheta,iphi,ivpar) +
-1./2. * (posx) * (posx-1.) * (posx-3.) *
FVAL(f0,ir-1+2,itheta,iphi,ivpar) +
1./6. * (posx) * (posx-1.) * (posx-2.) *
FVAL(f0,ir-1+3,itheta,iphi,ivpar);
}
}
}
}
TIMER_END(advec1D);
return 0;
}
int geom_init(geom_t* geom) {
geom->thetamin = 0.;
geom->dtheta = 2*M_PI/NTHETA;
geom->phimin = 0.;
geom->dphi = 2*M_PI/NPHI;
geom->dr = 2*M_PI/NR;
return 0;
}
int main(int argc, char **argv) {
geom_t geom;
double *fn, *fnp1;
double timef;
long long int i, sizebytes, real_nbbytes, nbops;
geom_init( &geom );
sizebytes = sizeof(double)*ALLOCSIZER*NTHETA*NPHI*NVPAR;
real_nbbytes = sizeof(double)*NR*NTHETA*NPHI*NVPAR;
nbops = NR*NTHETA*NPHI*NVPAR*7;
fn = (double*) _mm_malloc(sizebytes,64);
fnp1 = (double*) _mm_malloc(sizebytes,64);
// printf( "deb %p %p\n", fn, fnp1);
fn_init( fn, &geom );
for (i=0; i<NBREPEAT; i++) {
#ifdef _INTRIN_
fn_advec_int(fn, fnp1, &geom);
#else
fn_advec( fn, fnp1, &geom);
#endif
}
fn_verif( fnp1, &geom );
TIMER_PRINT_LIST(1);
timef = (timer_list[0][1])->ldiff_val*1000;
printf( "Time %.1f nano s, Bandwidth %.1f GB/s, GFLOps %.1f\n",timef,2*real_nbbytes/timef,nbops/timef);
}First include BOAST in the script
require 'BOAST'
include BOASTBOAST can handle the timing, so we can ignore the timing part of the original code.
Declare the constants used by the code.
NR=128
NTHETA=128
NVPAR=32
NPHI=32
DECNR=8
ALLOCSIZER=(2*DECNR+NR)Create a reference implementation we can compare against. We can use this to know if an optimization produces invalid results. We are using C code, so we will use C as the language instead of Fortran or CL.
def generate_reference()
push_env( :lang => C )Still inside the reference function, generate_reference, we will
create one code block for each part of our reference implementation.
We start by copying the macros and typedefs:
macro_ref = <<EOF
#ifndef NBREPEAT
#define NBREPEAT 2
#endif
#ifndef NR
#define NR 128
#endif
#ifndef NTHETA
#define NTHETA 128
#endif
#ifndef NVPAR
#define NVPAR 32
#endif
#ifndef NPHI
#define NPHI 32
#endif
#define DECNR 8
#define ALLOCSIZER (2*DECNR+NR)
#define FVAL(f,i1,i2,i3,i4) \
f[DECNR+i1+ALLOCSIZER*(i2+NTHETA*(i3+NPHI*(i4)))]
typedef struct {
double thetamin, dtheta;
double phimin, dphi;
double rmin, dr;
double vparmin, dvpar;
double *thetatmp;
double *phitmp;
double *rtmp;
} geom_t;
EOFWe do the same for all functions.
fn_advec, which computes the Lagrange:
code_ref= <<EOF
int fn_advec(double *f0, double *f1, geom_t *geom) {
int ivpar, iphi, itheta, ir;
double numres, posx;
double coef0, coef1, coef2, coef3;
__assume_aligned(f0, 64);
__assume_aligned(f1, 64);
#pragma omp parallel private(ir,itheta,iphi,ivpar, \
numres,coef0,coef1,coef2,coef3,posx)
#pragma omp for schedule(static) collapse(3)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,ir-DECNR,itheta,iphi,ivpar) = FVAL(f0,NR-DECNR+ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,NR+ir,itheta,iphi,ivpar) = FVAL(f0,ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<NR; ir++) {
posx = 1.5;
FVAL(f1,ir,itheta,iphi,ivpar) =
-1./6. * (posx-1.) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+0,itheta,iphi,ivpar) +
1./2. * (posx) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+1,itheta,iphi,ivpar) +
-1./2. * (posx) * (posx-1.) * (posx-3.) *
FVAL(f0,ir-1+2,itheta,iphi,ivpar) +
1./6. * (posx) * (posx-1.) * (posx-2.) *
FVAL(f0,ir-1+3,itheta,iphi,ivpar);
}
}
}
}
return 0;
}
EOFfn_init, responsible for initialization:
init_ref = <<EOF
int fn_init(double *f, geom_t *geom) {
int ivpar, iphi, itheta,ir;
double rval, thval, pval, vval;
geom->rtmp = malloc(NR*sizeof(double));
geom->thetatmp = malloc(NTHETA*sizeof(double));
geom->phitmp = malloc(NPHI*sizeof(double));
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr );
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,rval,thval,pval,vval)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma ivdep
for (ir=0; ir<NR; ir++) {
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
FVAL(f,ir,itheta,iphi,ivpar) = rval * thval * pval * vval;
}
}
}
}
return 0;
}
EOFcode_verif, which verifies the validity of the results:
code_verif = <<EOF
int fn_verif(double *f, geom_t *geom) {
int ivpar, iphi, itheta, ir;
int64_t count, modulo;
double rval, thval, pval, vval;
double numres, exact;
modulo = NR*NTHETA*NPHI*NVPAR/10;
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr +.5*geom->dr);
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,count,rval,thval,pval,vval, \
numres,exact)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
for (ir=0; ir<NR; ir++) {
count=ir+NR*(itheta+NTHETA*(iphi+NPHI*ivpar));
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
numres = FVAL(f,ir,itheta,iphi,ivpar);
exact = rval * thval * pval * vval;
if (!(fabs(numres-exact) < 1.e-4)) {
#pragma omp critical
{
printf( "ERROR! at %d %d %d %d, %.5e %.5e %.5e\\n",
ir,itheta,iphi,ivpar,numres,exact,numres-exact );
exit(2);
}
} else {
if (count%modulo == 0) {
#pragma omp critical
{
// printf( "OK %d %d %d %d, %.5e %.5e %.5e\\n",
// ir,itheta,iphi,ivpar,numres,exact,numres-exact );
}
}
}
}
}
}
}
return 0;
}
EOFWe now declare the input and output variables f, f0, and
f1. Notice while in the reference code these are of type double,
in BOAST that type is called Real. These variables have more than
one dimension, whose sizes are defined with Dim.
Input variables, which are sent to the kernel, must be specified with :dir => :in.
Output variables, which are calculated by the kernel, must be specified with :dir => :out.
If a variable is used both for input and output, use :dir => :inout.
f = Real( "f", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out)
f0 = Real( "f0", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :in)
f1 = Real( "f1", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out)Notice how the name of the variables appears in two places. For
instance, in /f = Real("f", ...) the first f is the name used by
our script and the second “f” is the name used inside the kernel.
We also need a struct: geom. We specified this struct in the
reference code, but that was in the C code. We need to provide an
equivalent specification our script can access:
geom = CStruct( "geom", :type_name => "geom_t", :members => [
Real( "thetamin"),
Real( "dtheta"),
Real( "phimin"),
Real( "dphi"),
Real( "rmin"),
Real( "dr"),
Real( "vparmin"),
Real( "dvpar"),
Real( "thetatmp", :dim => [Dim(NTHETA)]),
Real( "phitmp", :dim => [Dim(NPHI)]),
Real( "rtmp", :dim => [Dim(NR)])
],
:dim => [Dim(1)])Now that everything is in place we create one kernel for each function. We start by choosing a name and defining what types of parameters are accepted and what type is returned:
fn_init
p_init = Procedure("fn_init",[f,geom], :return => Int("a"))Again, the name appears twice: p_init is the name used by our script and fn_init the internal name. The parameters used by the kernel (f, geom) are passed inside a list ([]) as the second argument. Lastly, the return value is given as an Int.
Now that we declared the function we create a kernel object and give it the function declaration:
k_init = CKernel::new
k_init.procedure = p_initThe kernel still lacks the function code. The code is sent to the kernel with get_output.print. We already have the code in variables so let’s send that to get_output.print:
get_output.print macro_ref
get_output.print init_refThe same process is repeated for the other functions: fn_advec and
fn_verif.
fn_advec
p = Procedure("fn_advec",[f0,f1,geom], :return => Int("a"))
k = CKernel::new
k.procedure = p
get_output.print macro_ref
get_output.print code_reffn_verif
p_verif = Procedure("fn_verif",[f,geom], :return => Int("a"))
k_verif = CKernel::new
k_verif.procedure = p_verif
get_output.print macro_ref
get_output.print code_verifWe pop the lang we defined before and return the kernels.
pop_env(:lang)
return [k_init, k, k_verif]
endNow that the reference implementation is over. We can start writing our optimized kernel.
We start by creating a new function, generate_fn_advec and defining
the defaults for our parameters. Our parameters are:
vector_pragmas- enables or disables the use of #pragma vector
omp_num_threads- number of threads
nontemporal- the use or not of #pragma vector nontemporal
unroll- manual level of loop unrolling
Notice this function receives options as a parameter, allowing the caller to choose a different set of options than those defined below:
def generate_fn_advec(options = {})
default_options = { :vector_pragmas => false, :omp_num_threads => nil, :nontemporal => true, :unroll => false }
options = default_options.merge( options )
p optionsWe declare what variables this kernel uses. They are:
f0- double *
f1- double *
geom- struct
f0 = Real( "f0", :dim => [Dim(-DECNR,ALLOCSIZER-DECNR-1),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :inout, :align => 64)
f1 = Real( "f1", :dim => [Dim(-DECNR,ALLOCSIZER-DECNR-1),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out, :align => 64)
geom = CStruct( "geom", :type_name => "geom_t", :members => [
Real( "thetamin"),
Real( "dtheta"),
Real( "phimin"),
Real( "dphi"),
Real( "rmin"),
Real( "dr"),
Real( "vparmin"),
Real( "dvpar"),
Real( "thetatmp", :dim => [Dim(NTHETA)]),
Real( "phitmp", :dim => [Dim(NPHI)]),
Real( "rtmp", :dim => [Dim(NR)])
],
:dim => [Dim(1)])Build #pragma vector. This function allows the use of no vector
pragma, vector always, and vector always and nontemporal.
What it does is output the pragma lines only if they are in the
options. For instance, if options[:vector_pragmas] is false, it won’t
output anything. Otherwise, it will output #pragma vector always. If
options[:nontemporal] is true as well, it will also output #pragma
vector nontemporal.
vector_pragmas = lambda {
if options[:vector_pragmas] then
pr Pragma(:vector, "always")
pr Pragma(:vector, "nontemporal") if options[:nontemporal]
end
}Now we create the function using the different combinations of
parameters. Notice the use of options[:NAME] to generate different
code depending on the parameters being tested.
Notice how here the variables do not specify a direction (e.g. :dir => :in). The reason for that is these variables are local to the function.
p = Procedure("fn_advec",[f0,f1,geom], :return => Int("a")) {
ivpar = Int(:ivpar)
iphi = Int(:iphi)
itheta = Int(:itheta)
ir = Int(:ir)
decl ivpar, iphi, itheta, ir
numres = Real(:numres)
posx = Real(:posx)
decl numres, posx
coefs = (0..3).collect { |i|
Real("coef#{i}")
}
decl *coefs
pr OpenMP::Parallel( :private => [ir,itheta,iphi,ivpar,numres,posx]+coefs, :num_threads => options[:omp_num_threads] ) {
pr OpenMP::For( :schedule => "static", :collapse => 3 )
pr For(ivpar, 0, NVPAR-1) {
pr For(iphi, 0, NPHI-1) {
pr For(itheta, 0, NTHETA-1) {
for1 = For(ir, 0, DECNR-1) {
pr f0[ir-DECNR,itheta,iphi,ivpar] === f0[ir+NR-DECNR,itheta,iphi,ivpar]
}
for2 = For(ir, 0, DECNR-1) {
pr f0[ir+NR,itheta,iphi,ivpar] === f0[ir,itheta,iphi,ivpar]
}
if options[:unroll] then
pr for1.unroll
pr for2.unroll
else
vector_pragmas.call
pr for1
vector_pragmas.call
pr for2
end
vector_pragmas.call
pr For(ir, 0, NR-1) {
pr posx === 1.5
pr f1[ir,itheta,iphi,ivpar] ===
(-1.0/6.0).to_var * (posx-1.0) * (posx-2.0) * (posx-3.0) * f0[ir-1+0,itheta,iphi,ivpar] +
(1.0/2.0).to_var * (posx) * (posx-2.0) * (posx-3.0) * f0[ir-1+1,itheta,iphi,ivpar] +
(-1.0/2.0).to_var * (posx) * (posx-1.0) * (posx-3.0) * f0[ir-1+2,itheta,iphi,ivpar] +
(1.0/6.0).to_var * (posx) * (posx-1.0) * (posx-2.0) * f0[ir-1+3,itheta,iphi,ivpar]
}
}
}
}
}
pr Int(:a) === 0
}Now that the code is finished, we create a kernel and return it.
k = CKernel::new
k.procedure = p
pr p
return k
endWe will repeat the kernel 32 times, and start arrays at 0.
nbrepeat = 32
set_array_start(0)Compile the reference code with OpenMP enabled.
k_init, k_ref, k_verif = generate_reference
puts k_ref
k_init.build(:OPENMP => true)
k_verif.build(:OPENMP => true)
k_ref.build(:OPENMP => true)Create input data.
fn = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
fnp1 = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
fnp1_ref = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
geo = NArray::float(11)Execute the reference implementation 32 times and store the results.
k_init.run(fn, geo)
stats = []
nbrepeat.times {
stats.push k_ref.run(fn, fnp1_ref, geo)[:duration]
}
p stats.sort!
stats = k_verif.run(fnp1_ref, geo)Specify the values for each of our optimization parameters.
opt_space = OptimizationSpace::new( :vector_pragmas => [ true, false ],
:omp_num_threads => 1..6,
:nontemporal => [true, false],
:unroll => [true, false] )Run the different implementation versions. They will be run out of order and using all combinations of parameters.
optimizer = BruteForceOptimizer::new(opt_space, :randomize => true)
puts optimizer.optimize { |options|
k = generate_fn_advec(options)
# puts k
k.build(:OPENMP => true)
stats = []
nbrepeat.times {
stats.push k.run(fn, fnp1, geo)[:duration]
}Compare against the reference results to be sure we obtained valid results.
diff = (fnp1 - fnp1_ref).abs
puts diff.max
#k_verif.run(fnp1, geo)Of all the 32 replications, output the one with the lowest execution time for this combination of parameters.
best = stats.sort.first
puts best
best
}require 'BOAST'
include BOAST
NR=128
NTHETA=128
NVPAR=32
NPHI=32
DECNR=8
ALLOCSIZER=(2*DECNR+NR)
def generate_reference()
push_env( :lang => C )
macro_ref = <<EOF
#ifndef NBREPEAT
#define NBREPEAT 2
#endif
#ifndef NR
#define NR 128
#endif
#ifndef NTHETA
#define NTHETA 128
#endif
#ifndef NVPAR
#define NVPAR 32
#endif
#ifndef NPHI
#define NPHI 32
#endif
#define DECNR 8
#define ALLOCSIZER (2*DECNR+NR)
#define FVAL(f,i1,i2,i3,i4) \
f[DECNR+i1+ALLOCSIZER*(i2+NTHETA*(i3+NPHI*(i4)))]
typedef struct {
double thetamin, dtheta;
double phimin, dphi;
double rmin, dr;
double vparmin, dvpar;
double *thetatmp;
double *phitmp;
double *rtmp;
} geom_t;
EOF
code_ref= <<EOF
int fn_advec(double *f0, double *f1, geom_t *geom) {
int ivpar, iphi, itheta, ir;
double numres, posx;
double coef0, coef1, coef2, coef3;
__assume_aligned(f0, 64);
__assume_aligned(f1, 64);
#pragma omp parallel private(ir,itheta,iphi,ivpar, \
numres,coef0,coef1,coef2,coef3,posx)
#pragma omp for schedule(static) collapse(3)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,ir-DECNR,itheta,iphi,ivpar) = FVAL(f0,NR-DECNR+ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<DECNR; ir++) {
FVAL(f0,NR+ir,itheta,iphi,ivpar) = FVAL(f0,ir,itheta,iphi,ivpar);
}
#pragma vector always
#pragma vector nontemporal
for (ir=0; ir<NR; ir++) {
posx = 1.5;
FVAL(f1,ir,itheta,iphi,ivpar) =
-1./6. * (posx-1.) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+0,itheta,iphi,ivpar) +
1./2. * (posx) * (posx-2.) * (posx-3.) *
FVAL(f0,ir-1+1,itheta,iphi,ivpar) +
-1./2. * (posx) * (posx-1.) * (posx-3.) *
FVAL(f0,ir-1+2,itheta,iphi,ivpar) +
1./6. * (posx) * (posx-1.) * (posx-2.) *
FVAL(f0,ir-1+3,itheta,iphi,ivpar);
}
}
}
}
return 0;
}
EOF
init_ref = <<EOF
int fn_init(double *f, geom_t *geom) {
int ivpar, iphi, itheta,ir;
double rval, thval, pval, vval;
geom->rtmp = malloc(NR*sizeof(double));
geom->thetatmp = malloc(NTHETA*sizeof(double));
geom->phitmp = malloc(NPHI*sizeof(double));
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr );
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,rval,thval,pval,vval)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
#pragma vector always
#pragma ivdep
for (ir=0; ir<NR; ir++) {
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
FVAL(f,ir,itheta,iphi,ivpar) = rval * thval * pval * vval;
}
}
}
}
return 0;
}
EOF
code_verif = <<EOF
int fn_verif(double *f, geom_t *geom) {
int ivpar, iphi, itheta, ir;
int64_t count,lagrange1d.org modulo;
double rval, thval, pval, vval;
double numres, exact;
modulo = NR*NTHETA*NPHI*NVPAR/10;
for (iphi=0; iphi<NPHI; iphi++) geom->phitmp[iphi]=sin( geom->phimin + iphi *geom->dphi );
for (itheta=0; itheta<NTHETA; itheta++) geom->thetatmp[itheta]=sin( geom->thetamin + itheta*geom->dtheta + geom->dtheta*.5);
for (ir=0; ir<NR; ir++) geom->rtmp[ir] = sin( ir*geom->dr +.5*geom->dr);
#pragma omp parallel for schedule(static) private(ir,itheta,iphi,ivpar,count,rval,thval,pval,vval, \
numres,exact)
for (ivpar=0; ivpar<NVPAR; ivpar++) {
for (iphi=0; iphi<NPHI; iphi++) {
for (itheta=0; itheta<NTHETA; itheta++) {
for (ir=0; ir<NR; ir++) {
count=ir+NR*(itheta+NTHETA*(iphi+NPHI*ivpar));
rval = geom->rtmp[ir];
thval = geom->thetatmp[itheta];
pval = geom->phitmp[iphi];
vval = 1.;
numres = FVAL(f,ir,itheta,iphi,ivpar);
exact = rval * thval * pval * vval;
if (!(fabs(numres-exact) < 1.e-4)) {
#pragma omp critical
{
printf( "ERROR! at %d %d %d %d, %.5e %.5e %.5e\\n",
ir,itheta,iphi,ivpar,numres,exact,numres-exact );
exit(2);
}
} else {
if (count%modulo == 0) {
#pragma omp critical
{
// printf( "OK %d %d %d %d, %.5e %.5e %.5e\\n",
// ir,itheta,iphi,ivpar,numres,exact,numres-exact );
}
}
}
}
}
}
}
return 0;
}
EOF
f = Real( "f", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out)
f0 = Real( "f0", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :in)
f1 = Real( "f1", :dim => [Dim(ALLOCSIZER),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out)
geom = CStruct( "geom", :type_name => "geom_t", :members => [
Real( "thetamin"),
Real( "dtheta"),
Real( "phimin"),
Real( "dphi"),
Real( "rmin"),
Real( "dr"),
Real( "vparmin"),
Real( "dvpar"),
Real( "thetatmp", :dim => [Dim(NTHETA)]),
Real( "phitmp", :dim => [Dim(NPHI)]),
Real( "rtmp", :dim => [Dim(NR)])
],
:dim => [Dim(1)])
File::open("protolag1d.c") { |f|
source_ref = f.read
}
p_init = Procedure("fn_init",[f,geom], :return => Int("a"))
k_init = CKernel::new
k_init.procedure = p_init
get_output.print macro_ref
get_output.print init_ref
p = Procedure("fn_advec",[f0,f1,geom], :return => Int("a"))
k = CKernel::new
k.procedure = p
get_output.print macro_ref
get_output.print code_ref
p_verif = Procedure("fn_verif",[f,geom], :return => Int("a"))
k_verif = CKernel::new
k_verif.procedure = p_verif
get_output.print macro_ref
get_output.print code_verif
pop_env(:lang)
return [k_init, k, k_verif]
end
def generate_fn_advec(options = {})
default_options = { :vector_pragmas => false, :omp_num_threads => nil, :nontemporal => true, :unroll => false }
options = default_options.merge( options )
p options
f0 = Real( "f0", :dim => [Dim(-DECNR,ALLOCSIZER-DECNR-1),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :inout, :align => 64)
f1 = Real( "f1", :dim => [Dim(-DECNR,ALLOCSIZER-DECNR-1),Dim(NTHETA),Dim(NPHI),Dim(NVPAR)], :dir => :out, :align => 64)
geom = CStruct( "geom", :type_name => "geom_t", :members => [
Real( "thetamin"),
Real( "dtheta"),
Real( "phimin"),
Real( "dphi"),
Real( "rmin"),
Real( "dr"),
Real( "vparmin"),
Real( "dvpar"),
Real( "thetatmp", :dim => [Dim(NTHETA)]),
Real( "phitmp", :dim => [Dim(NPHI)]),
Real( "rtmp", :dim => [Dim(NR)])
],
:dim => [Dim(1)])
vector_pragmas = lambda {
if options[:vector_pragmas] then
pr Pragma(:vector, "always")
pr Pragma(:vector, "nontemporal") if options[:nontemporal]
end
}
p = Procedure("fn_advec",[f0,f1,geom], :return => Int("a")) {
ivpar = Int(:ivpar)
iphi = Int(:iphi)
itheta = Int(:itheta)
ir = Int(:ir)
decl ivpar, iphi, itheta, ir
numres = Real(:numres)
posx = Real(:posx)
decl numres, posx
coefs = (0..3).collect { |i|
Real("coef#{i}")
}
decl *coefs
pr OpenMP::Parallel( :private => [ir,itheta,iphi,ivpar,numres,posx]+coefs, :num_threads => options[:omp_num_threads] ) {
pr OpenMP::For( :schedule => "static", :collapse => 3 )
pr For(ivpar, 0, NVPAR-1) {
pr For(iphi, 0, NPHI-1) {
pr For(itheta, 0, NTHETA-1) {
for1 = For(ir, 0, DECNR-1) {
pr f0[ir-DECNR,itheta,iphi,ivpar] === f0[ir+NR-DECNR,itheta,iphi,ivpar]
}
for2 = For(ir, 0, DECNR-1) {
pr f0[ir+NR,itheta,iphi,ivpar] === f0[ir,itheta,iphi,ivpar]
}
if options[:unroll] then
pr for1.unroll
pr for2.unroll
else
vector_pragmas.call
pr for1
vector_pragmas.call
pr for2
end
vector_pragmas.call
pr For(ir, 0, NR-1) {
pr posx === 1.5
pr f1[ir,itheta,iphi,ivpar] ===
(-1.0/6.0).to_var * (posx-1.0) * (posx-2.0) * (posx-3.0) * f0[ir-1+0,itheta,iphi,ivpar] +
(1.0/2.0).to_var * (posx) * (posx-2.0) * (posx-3.0) * f0[ir-1+1,itheta,iphi,ivpar] +
(-1.0/2.0).to_var * (posx) * (posx-1.0) * (posx-3.0) * f0[ir-1+2,itheta,iphi,ivpar] +
(1.0/6.0).to_var * (posx) * (posx-1.0) * (posx-2.0) * f0[ir-1+3,itheta,iphi,ivpar]
}
}
}
}
}
pr Int(:a) === 0
}
k = CKernel::new
k.procedure = p
pr p
return k
end
nbrepeat = 32
set_array_start(0)
k_init, k_ref, k_verif = generate_reference
puts k_ref
k_init.build(:OPENMP => true)
k_verif.build(:OPENMP => true)
k_ref.build(:OPENMP => true)
fn = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
fnp1 = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
fnp1_ref = ANArray::float(64, ALLOCSIZER*NTHETA*NPHI*NVPAR)
geo = NArray::float(11)
k_init.run(fn, geo)
stats = []
nbrepeat.times {
stats.push k_ref.run(fn, fnp1_ref, geo)[:duration]
}
p stats.sort!
stats = k_verif.run(fnp1_ref, geo)
opt_space = OptimizationSpace::new( :vector_pragmas => [ true, false ],
:omp_num_threads => 1..6,
:nontemporal => [true, false],
:unroll => [true, false] )
optimizer = BruteForceOptimizer::new(opt_space, :randomize => true)
puts optimizer.optimize { |options|
k = generate_fn_advec(options)
# puts k
k.build(:OPENMP => true)
stats = []
nbrepeat.times {
stats.push k.run(fn, fnp1, geo)[:duration]
}
diff = (fnp1 - fnp1_ref).abs
puts diff.max
#k_verif.run(fnp1, geo)
best = stats.sort.first
puts best
best
}- node007 of mesocentre Aix-Marseille Université
- Westmere
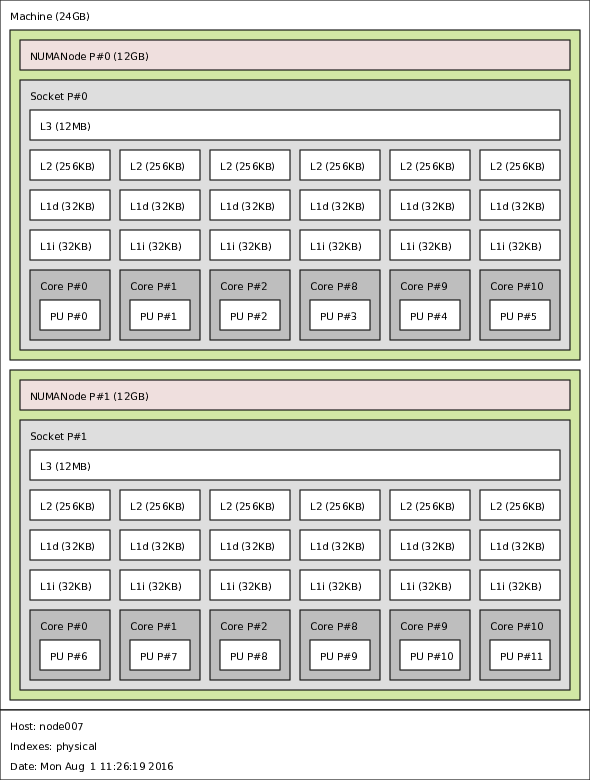
[bulldog@node008 ~]$ lscpu Architecture: x86_64 CPU op-mode(s): 32-bit, 64-bit Byte Order: Little Endian CPU(s): 24 On-line CPU(s) list: 0-11 Off-line CPU(s) list: 12-23 Thread(s) per core: 1 Core(s) per socket: 6 Socket(s): 2 NUMA node(s): 2 Vendor ID: GenuineIntel CPU family: 6 Model: 44 Stepping: 2 CPU MHz: 3066.815 BogoMIPS: 6133.14 Virtualization: VT-x L1d cache: 32K L1i cache: 32K L2 cache: 256K L3 cache: 12288K NUMA node0 CPU(s): 0-5 NUMA node1 CPU(s): 6-11
- NUMA
Let’s verify the effect of memory placement on the kernel:

As the figure shows, for this kernel interleave is the best of the tested NUMA policies. All figures below use this policy.
- Speedup

There is a small speedup up to 8 threads.
- Other Parameters

parapluie of Grid5000

Architecture: x86_64 CPU op-mode(s): 32-bit, 64-bit Byte Order: Little Endian CPU(s): 24 On-line CPU(s) list: 0-23 Thread(s) per core: 1 Core(s) per socket: 12 Socket(s): 2 NUMA node(s): 4 Vendor ID: AuthenticAMD CPU family: 16 Model: 9 Stepping: 1 CPU MHz: 1700.000 BogoMIPS: 3400.16 Virtualization: AMD-V L1d cache: 64K L1i cache: 64K L2 cache: 512K L3 cache: 5118K NUMA node0 CPU(s): 0-5 NUMA node1 CPU(s): 6-11 NUMA node2 CPU(s): 18-23 NUMA node3 CPU(s): 12-17
- NUMA

- Speedup-

- Other parameters

Node of the octodroid cluster on Mont-Blanc
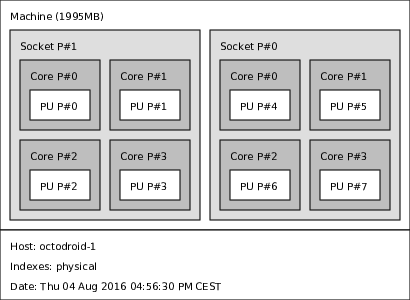
Architecture: armv7l Byte Order: Little Endian CPU(s): 8 On-line CPU(s) list: 0-7 Thread(s) per core: 1 Core(s) per socket: 4 Socket(s): 2 Model name: ARMv7 Processor rev 3 (v7l) CPU max MHz: 1400.0000 CPU min MHz: 200.0000
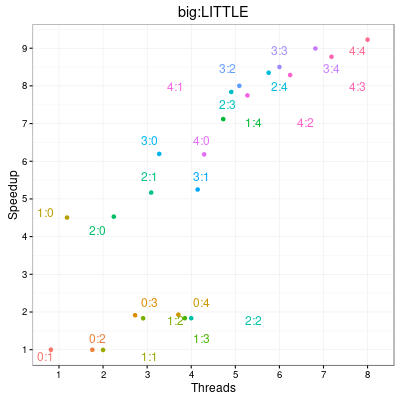
- Speedup for big and little cores

- Speedup
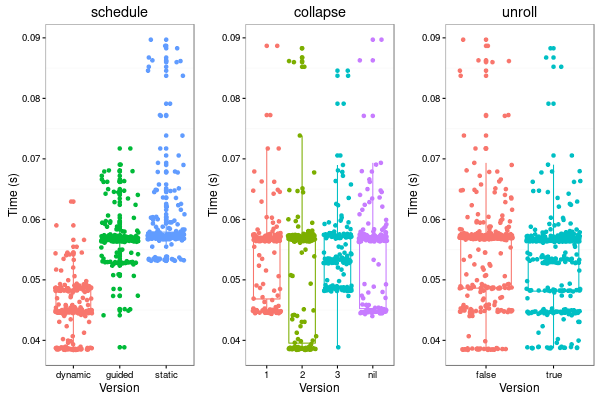
- Other parameters

Laptop

Architecture: x86_64 CPU op-mode(s): 32-bit, 64-bit Byte Order: Little Endian CPU(s): 8 On-line CPU(s) list: 0-7 Thread(s) per core: 2 Core(s) per socket: 4 Socket(s): 1 NUMA node(s): 1 Vendor ID: GenuineIntel CPU family: 6 Model: 58 Model name: Intel(R) Core(TM) i7-3720QM CPU @ 2.60GHz Stepping: 9 CPU MHz: 1203.109 CPU max MHz: 3600.0000 CPU min MHz: 1200.0000 BogoMIPS: 5185.09 Virtualization: VT-x L1d cache: 32K L1i cache: 32K L2 cache: 256K L3 cache: 6144K NUMA node0 CPU(s): 0-7 Flags: fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat pse36 clflush dts acpi mmx fxsr sse sse2 ss ht tm pbe syscall nx rdtscp lm constant_tsc arch_perfmon pebs bts rep_good nopl xtopology nonstop_tsc aperfmperf eagerfpu pni pclmulqdq dtes64 monitor ds_cpl vmx smx est tm2 ssse3 cx16 xtpr pdcm pcid sse4_1 sse4_2 x2apic popcnt tsc_deadline_timer aes xsave avx f16c rdrand lahf_lm epb tpr_shadow vnmi flexpriority ept vpid fsgsbase smep erms xsaveopt dtherm ida arat pln pts
Average execution time and energy for all combinations of parameters.

Execution time and energy consumption for the three fastest and three most efficient kernels:
