Docs-1

SciML · Jan 10, 2024 · 3d11a70 · 3d11a70
1 parent 8008f3a
commit 3d11a70
Show file tree

Hide file tree

Showing 8 changed files with 181 additions and 36 deletions.
diff --git a/docs/src/manual/bpinns.md b/docs/src/manual/bpinns.md
@@ -0,0 +1,22 @@
+# `BayesianPINN` Discretizer for PDESystems
+
+Using the Bayesian PINNs solvers, we can solve general nonlinear PDEs,ODEs and Also simultaniously perform PDE,ODE parameter Estimation.
+
+Note: The BPINN PDE solver also works for ODEs defined using ModelingToolkit, [ModelingToolkit.jl PDESystem documentation](https://docs.sciml.ai/ModelingToolkit/stable/systems/PDESystem/). Despite this the ODE specific BPINN solver `BNNODE` [refer](https://docs.sciml.ai/NeuralPDE/dev/manual/ode/#NeuralPDE.BNNODE) exists and uses `NeuralPDE.advancedhmc_pinn_ode` at a lower level.
+
+# `BayesianPINN` Discretizer for PDESystems and lower level Bayesian PINN Solver calls for PDEs and ODEs.
+
+```@docs
+NeuralPDE.BayesianPINN
+NeuralPDE.advancedhmc_pinn_pde
+NeuralPDE.advancedhmc_pinn_ode
+```
+
+## `symbolic_discretize` for `BayesianPINN` and lower level interface.
+
+```@docs
+SciMLBase.symbolic_discretize(::PDESystem, ::NeuralPDE.AbstractPINN)
+NeuralPDE.BPINNstats
+NeuralPDE.BPINNsolution
+```
+
diff --git a/docs/src/manual/pinns.md b/docs/src/manual/pinns.md
@@ -29,10 +29,10 @@ NeuralPDE.Phi
 SciMLBase.discretize(::PDESystem, ::NeuralPDE.PhysicsInformedNN)
 ```
 
-## `symbolic_discretize` and the lower-level interface
+## `symbolic_discretize` for `PhysicsInformedNN` and the lower-level interface
 
 ```@docs
-SciMLBase.symbolic_discretize(::PDESystem, ::NeuralPDE.PhysicsInformedNN)
+SciMLBase.symbolic_discretize(::PDESystem, ::NeuralPDE.AbstractPINN)
 NeuralPDE.PINNRepresentation
 NeuralPDE.PINNLossFunctions
 ```
diff --git a/docs/src/tutorials/low_level.md → docs/src/tutorials/low_level_1.md b/docs/src/tutorials/low_level.md → docs/src/tutorials/low_level_1.md
@@ -1,4 +1,4 @@
-# Investigating `symbolic_discretize` with the 1-D Burgers' Equation
+# Investigating `symbolic_discretize` with the `PhysicsInformedNN` Discretizer for the 1-D Burgers' Equation
 
 Let's consider the Burgers' equation:
 

diff --git a/docs/src/tutorials/low_level_2.md b/docs/src/tutorials/low_level_2.md
@@ -0,0 +1,75 @@
+# Using `ahmc_bayesian_pinn_pde` with the `BayesianPINN` Discretizer for the 1-D Burgers' Equation
+
+Let's consider the Burgers' equation:
+
+```math
+\begin{gather*}
+∂_t u + u ∂_x u - (0.01 / \pi) ∂_x^2 u = 0 \, , \quad x \in [-1, 1], t \in [0, 1] \, , \\
+u(0, x) = - \sin(\pi x) \, , \\
+u(t, -1) = u(t, 1) = 0 \, ,
+\end{gather*}
+```
+
+with Bayesian Physics-Informed Neural Networks. Here is an example of using `BayesianPINN` discretization with `ahmc_bayesian_pinn_pde` :
+
+```@example low_level_2
+using NeuralPDE, Lux, ModelingToolkit
+import ModelingToolkit: Interval, infimum, supremum
+
+@parameters t, x
+@variables u(..)
+Dt = Differential(t)
+Dx = Differential(x)
+Dxx = Differential(x)^2
+
+#2D PDE
+eq = Dt(u(t, x)) + u(t, x) * Dx(u(t, x)) - (0.01 / pi) * Dxx(u(t, x)) ~ 0
+
+# Initial and boundary conditions
+bcs = [u(0, x) ~ -sin(pi * x),
+    u(t, -1) ~ 0.0,
+    u(t, 1) ~ 0.0,
+    u(t, -1) ~ u(t, 1)]
+
+# Space and time domains
+domains = [t ∈ Interval(0.0, 1.0),
+    x ∈ Interval(-1.0, 1.0)]
+# Discretization
+dx = 0.05
+# Neural network
+chain = Lux.Chain(Lux.Dense(2, 10, Lux.σ), Lux.Dense(10, 10, Lux.σ), Lux.Dense(10, 1))
+strategy = NeuralPDE.GridTraining([dx,dx])
+
+discretization = NeuralPDE.BayesianPINN([chain], strategy)
+
+@named pde_system = PDESystem(eq, bcs, domains, [x, t], [u(x, t)])
+
+sol1 = ahmc_bayesian_pinn_pde(pde_system,
+    discretization;
+    draw_samples = 100,
+    bcstd = [0.01, 0.03, 0.03, 0.01],
+    phystd = [0.01],
+    priorsNNw = (0.0, 10.0),
+    saveats = [1 / 100.0, 1 / 100.0],progress=true)
+```
+
+And some analysis:
+
+```@example low_level
+using Plots
+
+ts, xs = [infimum(d.domain):0.01:supremum(d.domain) for d in domains]
+u_predict_contourf = reshape([first(phi([t, x], res.u)) for t in ts for x in xs],
+                             length(xs), length(ts))
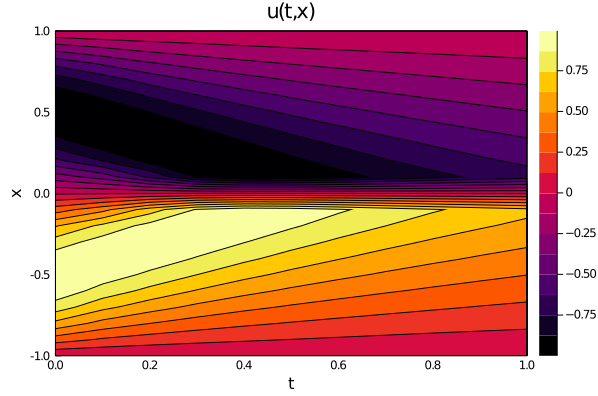
+plot(ts, xs, u_predict_contourf, linetype = :contourf, title = "predict")
+
+u_predict = [[first(phi([t, x], res.u)) for x in xs] for t in ts]
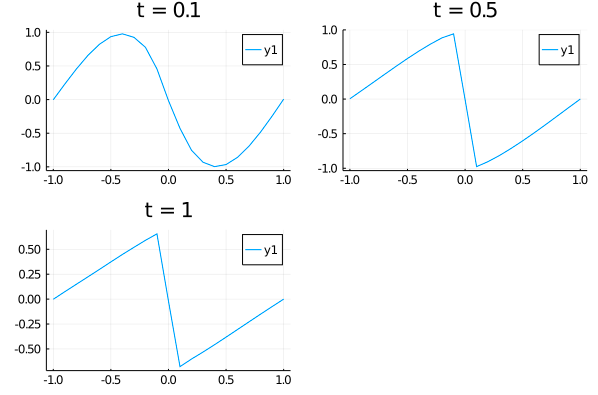
+p1 = plot(xs, u_predict[3], title = "t = 0.1");
+p2 = plot(xs, u_predict[11], title = "t = 0.5");
+p3 = plot(xs, u_predict[end], title = "t = 1");
+plot(p1, p2, p3)
+```
+
+![burgers](https://user-images.githubusercontent.com/12683885/90984874-a0870800-e580-11ea-9fd4-af8a4e3c523e.png)
+
+![burgers2](https://user-images.githubusercontent.com/12683885/90984856-8c430b00-e580-11ea-9206-1a88ebd24ca0.png)
diff --git a/src/advancedHMC_MCMC.jl b/src/advancedHMC_MCMC.jl
@@ -436,7 +436,6 @@ Incase you are only solving the Equations for solution, do not provide dataset
 
 ## Keyword Arguments
 * `strategy`: The training strategy used to choose the points for the evaluations. By default GridTraining is used with given physdt discretization.
-* `dataset`: Vector containing Vectors of corresponding u,t values 
 * `init_params`: intial parameter values for BPINN (ideally for multiple chains different initializations preferred)
 * `nchains`: number of chains you want to sample (random initialisation of params by default)
 * `draw_samples`: number of samples to be drawn in the MCMC algorithms (warmup samples are ~2/3 of draw samples)
@@ -469,7 +468,6 @@ Incase you are only solving the Equations for solution, do not provide dataset
 """
 
 """
-dataset would be (x̂,t)
 priors: pdf for W,b + pdf for ODE params
 """
 function ahmc_bayesian_pinn_ode(prob::DiffEqBase.ODEProblem, chain;

diff --git a/src/discretize.jl b/src/discretize.jl
@@ -389,14 +389,15 @@ end
 
 """
 ```julia
-prob = symbolic_discretize(pde_system::PDESystem, discretization::PhysicsInformedNN)
+prob = symbolic_discretize(pde_system::PDESystem, discretization::AbstractPINN)
 ```
 
 `symbolic_discretize` is the lower level interface to `discretize` for inspecting internals.
 It transforms a symbolic description of a ModelingToolkit-defined `PDESystem` into a
 `PINNRepresentation` which holds the pieces required to build an `OptimizationProblem`
-for [Optimization.jl](https://docs.sciml.ai/Optimization/stable) whose solution is the solution
-to the PDE.
+for [Optimization.jl](https://docs.sciml.ai/Optimization/stable) or a Likelihood Function
+used for HMC based Posterior Sampling Algorithms [AdvancedHMC.jl](https://turinglang.org/AdvancedHMC.jl/stable/)
+which is later optimized upon to give Solution or the Solution Distribution of the PDE.
 
 For more information, see `discretize` and `PINNRepresentation`.
 """

diff --git a/src/pinn_types.jl b/src/pinn_types.jl
@@ -17,7 +17,7 @@ end
 
 """This function is defined here as stubs to be overriden by the subpackage NeuralPDELogging if imported"""
 function logvector(logger, v::AbstractVector{R}, name::AbstractString,
-                   step::Integer) where {R <: Real}
+        step::Integer) where {R <: Real}
     nothing
 end
 
@@ -95,17 +95,17 @@ struct PhysicsInformedNN{T, P, PH, DER, PE, AL, ADA, LOG, K} <: AbstractPINN
     kwargs::K
 
     @add_kwonly function PhysicsInformedNN(chain,
-                                           strategy;
-                                           init_params = nothing,
-                                           phi = nothing,
-                                           derivative = nothing,
-                                           param_estim = false,
-                                           additional_loss = nothing,
-                                           adaptive_loss = nothing,
-                                           logger = nothing,
-                                           log_options = LogOptions(),
-                                           iteration = nothing,
-                                           kwargs...)
+            strategy;
+            init_params = nothing,
+            phi = nothing,
+            derivative = nothing,
+            param_estim = false,
+            additional_loss = nothing,
+            adaptive_loss = nothing,
+            logger = nothing,
+            log_options = LogOptions(),
+            iteration = nothing,
+            kwargs...)
         multioutput = chain isa AbstractArray
 
         if phi === nothing
@@ -134,23 +134,22 @@ struct PhysicsInformedNN{T, P, PH, DER, PE, AL, ADA, LOG, K} <: AbstractPINN
         new{typeof(strategy), typeof(init_params), typeof(_phi), typeof(_derivative),
             typeof(param_estim),
             typeof(additional_loss), typeof(adaptive_loss), typeof(logger), typeof(kwargs)}(chain,
-                                                                                            strategy,
-                                                                                            init_params,
-                                                                                            _phi,
-                                                                                            _derivative,
-                                                                                            param_estim,
-                                                                                            additional_loss,
-                                                                                            adaptive_loss,
-                                                                                            logger,
-                                                                                            log_options,
-                                                                                            iteration,
-                                                                                            self_increment,
-                                                                                            multioutput,
-                                                                                            kwargs)
+            strategy,
+            init_params,
+            _phi,
+            _derivative,
+            param_estim,
+            additional_loss,
+            adaptive_loss,
+            logger,
+            log_options,
+            iteration,
+            self_increment,
+            multioutput,
+            kwargs)
     end
 end
 
-
 """
 ```julia
 BayesianPINN(chain,
@@ -177,6 +176,9 @@ BayesianPINN(chain,
 
 ## Keyword Arguments
 
+* `Dataset`: A vector of matrix, each matrix for ith dependant
+  variable and first col in matrix is for dependant variables,
+  remaining coloumns for independant variables.
 * `init_params`: the initial parameters of the neural networks. This should match the
   specification of the chosen `chain` library. For example, if a Flux.chain is used, then
   `init_params` should match `Flux.destructure(chain)[1]` in shape. If `init_params` is not

diff --git a/test/BPINN_PDE_tests.jl b/test/BPINN_PDE_tests.jl
@@ -171,7 +171,7 @@ chain = Lux.Chain(Lux.Dense(dim, 9, Lux.σ), Lux.Dense(9, 9, Lux.σ), Lux.Dense(
 
 # Discretization
 dx = 0.05
-discretization=NeuralPDE.BayesianPINN([chain], GridTraining(dx))
+discretization = NeuralPDE.BayesianPINN([chain], GridTraining(dx))
 
 @named pde_system = PDESystem(eq, bcs, domains, [x, y], [u(x, y)])
 
@@ -198,4 +198,51 @@ diff_u = abs.(u_predict .- u_real)
 #     pmean(sol1.ensemblesol[1]),
 #     linetype = :contourf)
 # plot(sol1.timepoints[1][1, :], sol1.timepoints[1][2, :], u_real, linetype = :contourf)
-# plot(sol1.timepoints[1][1, :], sol1.timepoints[1][2, :], diff_u, linetype = :contourf)
+# plot(sol1.timepoints[1][1, :], sol1.timepoints[1][2, :], diff_u, linetype = :contourf)
+
+using NeuralPDE, Lux, ModelingToolkit
+import ModelingToolkit: Interval, infimum, supremum
+
+@parameters t, x
+@variables u(..)
+Dt = Differential(t)
+Dx = Differential(x)
+Dxx = Differential(x)^2
+
+#2D PDE
+eq = Dt(u(t, x)) + u(t, x) * Dx(u(t, x)) - (0.01 / pi) * Dxx(u(t, x)) ~ 0
+
+# Initial and boundary conditions
+bcs = [u(0, x) ~ -sin(pi * x),
+    u(t, -1) ~ 0.0,
+    u(t, 1) ~ 0.0,
+    u(t, -1) ~ u(t, 1)]
+
+# Space and time domains
+domains = [t ∈ Interval(0.0, 1.0),
+    x ∈ Interval(-1.0, 1.0)]
+# Discretization
+dx = 0.05
+# Neural network
+chain = Lux.Chain(Lux.Dense(2, 8, Lux.tanh), Lux.Dense(8, 8, Lux.tanh), Lux.Dense(8, 1))
+strategy = NeuralPDE.GridTraining([dx, dx])
+
+discretization = NeuralPDE.BayesianPINN([chain], strategy)
+
+@named pde_system = PDESystem(eq, bcs, domains, [x, t], [u(x, t)])
+
+sol1 = ahmc_bayesian_pinn_pde(pde_system,
+    discretization;
+    draw_samples = 200,
+    bcstd = [0.01, 0.01, 0.01, 0.01],
+    phystd = [0.01],
+    priorsNNw = (0.0, 10.0),
+    saveats = [1 / 100.0, 1 / 100.0], progress = true)
+
+using Plots, StatsPlots
+plotly()
+plot(sol1.timepoints[1][2, :], sol1.timepoints[1][1, :],
+    pmean(sol1.ensemblesol[1]),
+    linetype = :contourf)
+
+plot(sol1.timepoints[1][1, :], pmean(sol1.ensemblesol[1]))