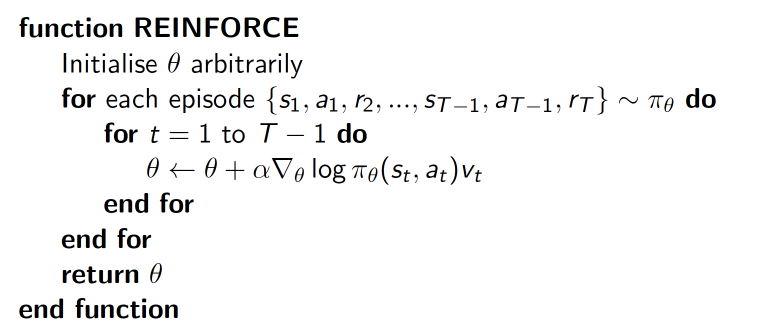Policy based Sequential Decision
别看底下有英文,真的很简单,不信你读😉
做Reinforcement Learning方向的,要明确其目标: 找到可以让agent获得最优回报的最优行为策略
- on-policy
- either discrete or continuous action spaces
Policy gradient输出不是 action 的 value, 而是具体的那一个 action, 这样 policy gradient 就跳过了 value 评估这个阶段, 对策略本身进行评估。
We must find the best parameters (θ) to maximize a score function, J(θ). $$ J(\theta)=E_{\pi_\theta}[\sum\gamma r] $$ There are two steps:
- Measure the quality of a π (policy) with a policy score function J(θ) (策略评估)
- Use policy gradient ascent to find the best parameter θ that improves our π. (策略提升)
-
episode environment with same start state
$s_1$ $$ J_1(\theta)=E_\pi[G_1=R_1+\gamma R_2+\gamma^2 R_3+\dots]=E_\pi (V(s_1)) $$ -
continuous environment (use the average value)
$$\begin{aligned} J_{avgv}(\theta)&=E_{\pi}(V(s))=\sum_{s\in \mathcal{S}} d^\pi (s)V^\pi(s)\&=\sum_{s\in \mathcal{S}} d^\pi (s) \sum_{a\in \mathcal{A}} \pi_\theta(a|s)Q^\pi(s,a) \end{aligned} $$
where
$d^\pi (s)=\dfrac{N(s)}{\sum_{s'}N(s')}$ ,$N(s)$ means Number of occurrences of the state,$\sum_{s'}N(s')$ represents Total number of occurrences of all state. So$d^\pi (s)$ 代表在策略$\pi_\theta$ 下马尔科夫链的平稳分布 (on-policy state distribution under π), 详见Policy Gradient Algorithms - lilianweng's blog👍 -
use the average reward per time step. The idea here is that we want to get the most reward per time step.
与我们惯用的梯度下降相反,这里用的是梯度上升! $$ \theta\leftarrow \theta + \alpha\nabla_\theta J(\theta) $$
Our score function J(θ) can be also defined as:
Since
我们将上一节的三种policy score function归纳为:
It provides a nice reformation of the derivative of the objective function to not involve the derivative of the state distribution
Proof: Policy Gradient Algorithms - lilianweng's blog👍
It is also hard to differentiating
分解
那么这个log的偏导怎么求呢?
在Coding的时候就是这段:
y = np.zeros([self.act_space])
y[act] = 1 # 制作离散动作空间,执行了的置1
self.gradients.append(np.array(y).astype('float32')-prob)
最后, 我们得到了VPG的更新方法:
对应的code就是, 这里对reward做了归一化:
def learn(self):
gradients = np.vstack(self.gradients)
rewards = np.vstack(self.rewards)
rewards = self.discount_rewards(rewards)
# reward归一化
rewards = (rewards - np.mean(rewards)) / (np.std(rewards) + 1e-7)
gradients *= rewards
X = np.squeeze(np.vstack([self.states]))
Y = self.act_probs + self.alpha * np.squeeze(np.vstack([gradients]))
REINFORCE: 一种基于整条回合数据的更新, remember that? Monte-Carlo method!
其中,$\nabla log \pi_{\theta}(s_t,a_t)v_t$可以理解为在状态
$s$ 对所选动作的$a$ 的吃惊度,$\pi_{\theta}(s_t,a_t)$概率越小,反向的$log(Policy(s,a))$ (即-log(P)) 反而越大. 如果在Policy(s,a)很小的情况下, 拿到了一个大的R, 也就是大的V, 那$\nabla log \pi_{\theta}(s_t,a_t)v_t$ 就更大, 表示更吃惊, (我选了一个不常选的动作, 却发现原来它能得到了一个好的 reward, 那我就得对我这次的参数进行一个大幅修改). 这就是吃惊度的物理意义.
VPG (OpenAI SpinningUp的定义)
可以发现引入了值函数/优势函数,这是后期改进之后的版本,使其可以用于非回合制的环境。
'''
用于回合更新的离散控制 REINFORCE
'''
class Skylark_VPG():
def __init__(self, env, alpha = 0.1, gamma = 0.6, epsilon=0.1, update_freq = 200):
self.obs_space = 80*80 # 视根据具体gym环境的state输出格式,具体分析
self.act_space = env.action_space.n
self.env = env
self.alpha = alpha # learning rate
self.gamma = gamma # discount rate
self.states = []
self.gradients = []
self.rewards = []
self.act_probs = []
self.total_step = 0
self.model = self._build_model()
self.model.summary()
def _build_model(self):
model = Sequential()
model.add(Reshape((1, 80, 80), input_shape=(self.obs_space,)))
model.add(Conv2D(32, (6, 6), activation="relu", strides=(3, 3),
padding="same", kernel_initializer="he_uniform"))
model.add(Flatten())
model.add(Dense(64, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(32, activation='relu', kernel_initializer='he_uniform'))
# softmax策略使用描述状态和行为的特征ϕ(s,a) 与参数\theta的线性组合来权衡一个行为发生的概率
# 输出为每个动作的概率
model.add(Dense(self.act_space, activation='softmax'))
opt = Adam(lr=self.alpha)
model.compile(loss='categorical_crossentropy', optimizer=opt)
return model
def choose_action(self, state):
state = state.reshape([1, self.obs_space])
act_prob = self.model.predict(state).flatten()
prob = act_prob / np.sum(act_prob)
self.act_probs.append(act_prob)
# 按概率选取动作
action = np.random.choice(self.act_space, 1, p=prob)[0]
return action, prob
def store_trajectory(self, s, a, r, prob):
y = np.zeros([self.act_space])
y[a] = 1 # 制作离散动作空间,执行了的置1
self.gradients.append(np.array(y).astype('float32')-prob)
self.states.append(s)
self.rewards.append(r)
def discount_rewards(self, rewards):
'''
从回合结束位置向前修正reward
'''
discounted_rewards = np.zeros_like(rewards)
running_add = 0
for t in reversed(range(0, rewards.size)):
if rewards[t] != 0:
running_add = 0
running_add = running_add * self.gamma + rewards[t]
discounted_rewards[t] = np.array(running_add)
return discounted_rewards
def learn(self):
gradients = np.vstack(self.gradients)
rewards = np.vstack(self.rewards)
rewards = self.discount_rewards(rewards)
# reward归一化
rewards = (rewards - np.mean(rewards)) / (np.std(rewards) + 1e-7)
gradients *= rewards
X = np.squeeze(np.vstack([self.states]))
Y = self.act_probs + self.alpha * np.squeeze(np.vstack([gradients]))
self.model.train_on_batch(X, Y)
self.states, self.act_probs, self.gradients, self.rewards = [], [], [], []
def train(self, num_episodes, batch_size = 128, num_steps = 100):
for i in range(num_episodes):
state = self.env.reset()
steps, penalties, reward, sum_rew = 0, 0, 0, 0
done = False
while not done:
# self.env.render()
state = preprocess(state)
action, prob = self.choose_action(state)
# Interaction with Env
next_state, reward, done, info = self.env.step(action)
self.store_trajectory(state, action, reward, prob)
sum_rew += reward
state = next_state
steps += 1
self.total_step += 1
if done:
self.learn()
print('Episode: {} | Avg_reward: {} | Length: {}'.format(i, sum_rew/steps, steps))
print("Training finished.")
Advantages
-
输出的这个 action 可以是一个连续值, 之前我们说到的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action. 而 policy gradient 可以在一个连续分布上选取 action.
-
Convergence: The problem with value-based methods is that they can have a big oscillation while training. This is because the choice of action may change dramatically for an arbitrarily small change in the estimated action values.
On the other hand, with policy gradient, we just follow the gradient to find the best parameters. We see a smooth update of our policy at each step.
Because we follow the gradient to find the best parameters, we’re guaranteed to converge on a local maximum (worst case) or global maximum (best case).
-
Policy gradients can learn stochastic policies
-
we don’t need to implement an exploration/exploitation trade off.
-
get rid of the problem of perceptual aliasing.
-
Disadvantages
- A lot of the time, they converge on a local maximum rather than on the global optimum.
- In a situation of Monte Carlo, waiting until the end of episode to calculate the reward.
- on-policy
- either discrete or continuous action spaces
TRPO译为信赖域策略优化,TRPO的出现是要解决VPG存在的问题的:VPG的更新步长
这让我想起了优化中对步长的估计:Armijo-Goldstein准则、Wolfe-Powell准则等。当然和TRPO关系不大。
TRPO有一个大胆的想法,要让更新后的策略回报函数单调不减。一个自然的想法是,将新策略所对应的回报函数表示成旧策略所对应的回报函数+其他项。下式就是TRPO的起手式:
-
$\eta$ 会被用作代价函数,毕竟在PG的梯度上升中,代价函数和回报函数等价 -
$A_\pi$ 为优势函数(这个会在A2C的章节讲到)
Proof: (也可以通过构造法反推) $$\begin{aligned} E_{\tau | \hat{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t} A_{\pi}\left(s_{t}, a_{t}\right)\right] &=E_{\tau | \hat{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(r(s)+\gamma V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_{t}\right)\right)\right] \ &=E_{\tau | \hat{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(r\left(s_{t}\right)\right)+\sum_{t=0}^{\infty} \gamma^{t}\left(\gamma V^{\pi}\left(s_{t+1}\right)-V^{\pi}\left(s_{t}\right)\right)\right] \ &=E_{\tau | \hat{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t}\left(r\left(s_{t}\right)\right)\right]+E_{s_{0}}\left[-V^{\pi}\left(s_{0}\right)\right] \ &=\eta(\hat{\pi})-\eta(\pi) \end{aligned}$$
由此,我们就实现了将新策略的回报表示为旧策略回报的目标。
有了起手式,我们在实际操作时候具体怎么计算呢?尤其是优势函数外那个期望的怎么处理?
将其分解成state和action的求和:
-
$\sum_{a} \hat{\pi}(a | s) \gamma^{t} A_{\pi}(s, a)$ 是在状态 s 时,计算动作 a 的边际分布 -
$\sum_{s} P\left(s_{t}=s | \hat{\pi}\right)$ 是在时间 t 时,求状态 s 的边际分布 -
$\sum_{t=0}^{\infty} \sum_{s} P\left(s_{t}=s | \hat{\pi}\right)$ 对整个时间序列求和。
定义
即有
这个公式在应用时也无法使用,因为状态 s 是根据新策略的分布产生的,而新策略又是我们要求的,这就导致了含有
-
一个简单的想法:用旧策略代替上式中的新策略
-
重要性采样来处理动作分布,也是TRPO的关键: $$\sum_{a} \hat{\pi}{\theta}\left(a | s{n}\right) A_{\theta_{o l d}}\left(s_{n}, a\right)=E_{a \sim q}\left[\frac{\hat{n}{\theta}\left(a | s{n}\right)}{\pi_{\theta_{o l d}}\left(a | s_{n}\right)} A_{\theta_{o l d}}\left(s_{n}, a\right)\right]$$ 得到
$\hat{\pi}$ 的一阶近似,替代回报函数$L_\pi(\hat{\pi})$ $$L_{\pi}(\hat{\pi})=\eta(\pi)+E_{s \sim \rho_{\theta_{o l d}}, a \sim \pi_{\theta_{o l d}}}\left[\frac{\hat{\pi}{\theta}\left(a | s{n}\right)}{\pi_{\theta_{o l d}}\left(a | s_{n}\right)} A_{\theta_{o l d}}\left(s_{n}, a\right)\right]$$
说完了损失函数的构建,那么步长到底怎么定呢?
$$\eta(\hat{\pi}) \geq L_{\pi}(\hat{\pi})-C D_{K L}^{\max }(\pi, \hat{\pi})$$ - 惩罚因子
$C=\frac{2 \epsilon_{V}}{(1-V)^{2}}$ -
$D_{K L}^{\max }(\pi, \hat{\pi})$ 为每个状态下动作分布的最大值
得到一个单调递增的策略序列:
$$M_{i}(\pi)=L_{\pi_{i}}(\tilde{\pi})-C D_{K L}^{\max }\left(\pi_{i}, \tilde{\pi}\right)$$ 可知
$$\eta\left(\pi_{i+1}\right) \geq M_{i}\left(\pi_{i+1}\right), and \quad \eta\left(\pi_{i}\right)=M_{i}\left(\pi_{i}\right)$$ $$\eta\left(\pi_{i+1}\right)-\eta\left(\pi_{i}\right) \geq M_{i}\left(\pi_{i+1}\right)-M\left(\pi_{i}\right)$$ 我们只需要在新策略序列中找到一个使
$M_i$ 最大的策略即可,对策略的搜寻就变成了优化问题:$$\max {\hat{\theta}}\left[L{\theta_{o l d}}-C D_{K L}^{\max }\left(\theta_{o l d}, \hat{\theta}\right)\right]$$
由于在实际中,C的限制会导致步长过小。因此,在TRPO原文中写作了约束优化问题:
$$\max {\theta} E{s \sim \rho_{\theta_{o l d}}, a \sim \pi_{o_{o l d}}}\left[\frac{\tilde{\pi}{\theta}\left(a | s{n}\right)}{\pi_{\theta_{o l d}}\left(a | s_{n}\right)} A_{\theta_{o l d}}\left(s_{n}, a\right)\right] \ s.t. \quad D_{K L}^{\max }\left(\theta_{o l d} || \theta\right) \leq \delta$$
- 惩罚因子
-
利用平均KL散度代替最大KL散度,最大KL不利于数值数值优化。
-
对约束问题二次近似,非约束问题一次近似,这是凸优化的一种常见改法。最后TRPO利用共轭梯度的方法进行最终的优化。
Q: 为什么觉得TRPO的叙述方式反了?私以为应该是在约束新旧策略的散度的前提下,找到使替代回报函数$L_\pi(\hat{\pi})$ 最大的
$\theta$ -> 转化为约束优化问题,这样就自然多了嘛。所以那一步惩罚因子的作用很让人迷惑,烦请大佬们在评论区解惑。
class Policy_Network(nn.Module):
def __init__(self, obs_space, act_space):
super(Policy_Network, self).__init__()
self.affine1 = nn.Linear(obs_space, 64)
self.affine2 = nn.Linear(64, 64)
self.action_mean = nn.Linear(64, act_space)
self.action_mean.weight.data.mul_(0.1)
self.action_mean.bias.data.mul_(0.0)
self.action_log_std = nn.Parameter(torch.zeros(1, act_space))
self.saved_actions = []
self.rewards = []
self.final_value = 0
def forward(self, x):
x = torch.tanh(self.affine1(x))
x = torch.tanh(self.affine2(x))
action_mean = self.action_mean(x)
action_log_std = self.action_log_std.expand_as(action_mean)
action_std = torch.exp(action_log_std)
return action_mean, action_log_std, action_std
class Value_Network(nn.Module):
def __init__(self, obs_space):
super(Value_Network, self).__init__()
self.affine1 = nn.Linear(obs_space, 64)
self.affine2 = nn.Linear(64, 64)
self.value_head = nn.Linear(64, 1)
self.value_head.weight.data.mul_(0.1)
self.value_head.bias.data.mul_(0.0)
def forward(self, x):
x = torch.tanh(self.affine1(x))
x = torch.tanh(self.affine2(x))
state_values = self.value_head(x)
return state_values
Transition = namedtuple('Transition', ('state', 'action', 'mask',
'reward', 'next_state'))
class Memory(object):
def __init__(self):
self.memory = []
def push(self, *args):
"""Saves a transition."""
self.memory.append(Transition(*args))
def sample(self):
return Transition(*zip(*self.memory))
def __len__(self):
return len(self.memory)
class Skylark_TRPO():
def __init__(self, env, alpha = 0.1, gamma = 0.6,
tau = 0.97, max_kl = 1e-2, l2reg = 1e-3, damping = 1e-1):
self.obs_space = 80*80
self.act_space = env.action_space.n
self.policy = Policy_Network(self.obs_space, self.act_space)
self.value = Value_Network(self.obs_space)
self.env = env
self.alpha = alpha # learning rate
self.gamma = gamma # discount rate
self.tau = tau #
self.max_kl = max_kl
self.l2reg = l2reg
self.damping = damping
self.replay_buffer = Memory()
self.buffer_size = 1000
self.total_step = 0
def choose_action(self, state):
state = torch.unsqueeze(torch.FloatTensor(state), 0)
action_mean, _, action_std = self.policy(Variable(state))
action = torch.normal(action_mean, action_std)
return action
def conjugate_gradients(self, Avp, b, nsteps, residual_tol=1e-10):
x = torch.zeros(b.size())
r = b.clone()
p = b.clone()
rdotr = torch.dot(r, r)
for i in range(nsteps):
_Avp = Avp(p)
alpha = rdotr / torch.dot(p, _Avp)
x += alpha * p
r -= alpha * _Avp
new_rdotr = torch.dot(r, r)
betta = new_rdotr / rdotr
p = r + betta * p
rdotr = new_rdotr
if rdotr < residual_tol:
break
return x
def linesearch(self, model,
f,
x,
fullstep,
expected_improve_rate,
max_backtracks=10,
accept_ratio=.1):
fval = f(True).data
print("fval before", fval.item())
for (_n_backtracks, stepfrac) in enumerate(.5**np.arange(max_backtracks)):
xnew = x + stepfrac * fullstep
set_flat_params_to(model, xnew)
newfval = f(True).data
actual_improve = fval - newfval
expected_improve = expected_improve_rate * stepfrac
ratio = actual_improve / expected_improve
print("a/e/r", actual_improve.item(), expected_improve.item(), ratio.item())
if ratio.item() > accept_ratio and actual_improve.item() > 0:
print("fval after", newfval.item())
return True, xnew
return False, x
def trpo_step(self, model, get_loss, get_kl, max_kl, damping):
loss = get_loss()
grads = torch.autograd.grad(loss, model.parameters())
loss_grad = torch.cat([grad.view(-1) for grad in grads]).data
def Fvp(v):
kl = get_kl()
kl = kl.mean() # 平均散度
grads = torch.autograd.grad(kl, model.parameters(), create_graph=True)
flat_grad_kl = torch.cat([grad.view(-1) for grad in grads])
kl_v = (flat_grad_kl * Variable(v)).sum()
grads = torch.autograd.grad(kl_v, model.parameters())
flat_grad_grad_kl = torch.cat([grad.contiguous().view(-1) for grad in grads]).data
return flat_grad_grad_kl + v * damping
stepdir = self.conjugate_gradients(Fvp, -loss_grad, 10)
shs = 0.5 * (stepdir * Fvp(stepdir)).sum(0, keepdim=True)
lm = torch.sqrt(shs / max_kl)
fullstep = stepdir / lm[0]
neggdotstepdir = (-loss_grad * stepdir).sum(0, keepdim=True)
print(("lagrange multiplier:", lm[0], "grad_norm:", loss_grad.norm()))
prev_params = get_flat_params_from(model)
success, new_params = self.linesearch(model, get_loss, prev_params, fullstep,
neggdotstepdir / lm[0])
set_flat_params_to(model, new_params)
return loss
def learn(self, batch_size=128):
batch = self.replay_buffer.sample()
rewards = torch.Tensor(batch.reward)
masks = torch.Tensor(batch.mask)
actions = torch.Tensor(np.concatenate(batch.action, 0))
states = torch.Tensor(batch.state)
values = self.value(Variable(states))
returns = torch.Tensor(actions.size(0),1)
deltas = torch.Tensor(actions.size(0),1)
advantages = torch.Tensor(actions.size(0),1)
prev_return = 0
prev_value = 0
prev_advantage = 0
for i in reversed(range(rewards.size(0))):
returns[i] = rewards[i] + self.gamma * prev_return * masks[i] # 计算了折扣累计回报
deltas[i] = rewards[i] + self.gamma * prev_value * masks[i] - values.data[i] # V - Q state value的偏差
advantages[i] = deltas[i] + self.gamma * self.tau * prev_advantage * masks[i] # 优势函数 A
prev_return = returns[i, 0]
prev_value = values.data[i, 0]
prev_advantage = advantages[i, 0]
targets = Variable(returns)
# Original code uses the same LBFGS to optimize the value loss
def get_value_loss(flat_params):
'''
构建替代回报函数 L_\pi(\hat{\pi})
'''
set_flat_params_to(self.value, torch.Tensor(flat_params))
for param in self.value.parameters():
if param.grad is not None:
param.grad.data.fill_(0)
values_ = self.value(Variable(states))
value_loss = (values_ - targets).pow(2).mean() # (f(s)-r)^2
# weight decay
for param in self.value.parameters():
value_loss += param.pow(2).sum() * self.l2reg # 参数正则项
value_loss.backward()
return (value_loss.data.double().numpy(), get_flat_grad_from(self.value).data.double().numpy())
# 使用 scipy 的 l_bfgs_b 算法来优化无约束问题
flat_params, _, opt_info = optimize.fmin_l_bfgs_b(func=get_value_loss, x0=get_flat_params_from(self.value).double().numpy(), maxiter=25)
set_flat_params_to(self.value, torch.Tensor(flat_params))
# 归一化优势函数
advantages = (advantages - advantages.mean()) / advantages.std()
action_means, action_log_stds, action_stds = self.policy(Variable(states))
fixed_log_prob = normal_log_density(Variable(actions), action_means, action_log_stds, action_stds).data.clone()
def get_loss(volatile=False):
'''
计算策略网络的loss
'''
if volatile:
with torch.no_grad():
action_means, action_log_stds, action_stds = self.policy(Variable(states))
else:
action_means, action_log_stds, action_stds = self.policy(Variable(states))
log_prob = normal_log_density(Variable(actions), action_means, action_log_stds, action_stds)
# -A * e^{\hat{\pi}/\pi_{old}}
action_loss = -Variable(advantages) * torch.exp(log_prob - Variable(fixed_log_prob))
return action_loss.mean()
def get_kl():
mean1, log_std1, std1 = self.policy(Variable(states))
mean0 = Variable(mean1.data)
log_std0 = Variable(log_std1.data)
std0 = Variable(std1.data)
kl = log_std1 - log_std0 + (std0.pow(2) + (mean0 - mean1).pow(2)) / (2.0 * std1.pow(2)) - 0.5
return kl.sum(1, keepdim=True)
self.trpo_step(self.policy, get_loss, get_kl, self.max_kl, self.damping)
def train(self, num_episodes, batch_size = 128, num_steps = 100):
for i in range(num_episodes):
state = self.env.reset()
steps, reward, sum_rew = 0, 0, 0
done = False
while not done and steps < num_steps:
state = preprocess(state)
action = self.choose_action(state)
action = action.data[0].numpy()
action_ = np.argmax(action)
# Interaction with Env
next_state, reward, done, info = self.env.step(action_)
next_state_ = preprocess(next_state)
mask = 0 if done else 1
self.replay_buffer.push(state, np.array([action]), mask, reward, next_state_)
if len(self.replay_buffer) > self.buffer_size:
self.learn(batch_size)
sum_rew += reward
state = next_state
steps += 1
self.total_step += 1
print('Episode: {} | Avg_reward: {} | Length: {}'.format(i, sum_rew/steps, steps))
print("Training finished.")
- on-policy
- either discrete or continuous action spaces
Same as the TRPO, the central idea of Proximal Policy Optimization is to avoid having too large policy update. To do that, we use a ratio that will tells us the difference between our new and old policy and clip this ratio from 0.8 to 1.2. Doing that will ensure that our policy update will not be too large.
The problem comes from the step size of gradient ascent:
- Too small, the training process was too slow
- Too high, there was too much variability in the training.
The idea is that PPO improves the stability of the Actor training by limiting the policy update at each training step.
把TRPO的约束转化为目标函数的罚项,并且能够自动地调整惩罚系数。
这么说 TRPO 那步惩罚因子是半成品,TRPO的完整版应该就是PPO1了。
$$L^{KLPEN}(\theta)=\hat{\mathbb{E}}{t}\left[\frac{\pi{\theta}\left(a_{t} | s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} | s_{t}\right)} \hat{A}{t}-\beta \operatorname{KL}\left[\pi{\theta_{\text {old }}}\left(\cdot | s_{t}\right), \pi_{\theta}\left(\cdot | s_{t}\right)\right]\right]$$
self.beta = tf.placeholder(tf.float32, None, 'lambda')
kl = tf.distributions.kl_divergence(old_nd, nd)
self.kl_mean = tf.reduce_mean(kl)
self.aloss = -(tf.reduce_mean(surr - self.beta * kl))
Keypoint:$\beta$参数跟随训练进程自调整:
if kl < self.kl_target / 1.5:
self.lam /= 2
elif kl > self.kl_target * 1.5:
self.lam *= 2
依靠对目标函数的专门裁剪来消除新策略远离旧策略的动机,代替KL散度。
To be able to do that PPO introduced a new objective function called “Clipped surrogate objective function” that will constraint the policy change in a small range using a clip.
Instead of using
- If
$r_t(θ)$ >1, it means that the action is more probable in the current policy than the old policy. - If
$r_t(θ)$ is between 0 and 1: it means that the action is less probable for current policy than for the old one.
As consequence, our new objective function could be: $$ L^{CPI}(\theta)=\hat{\mathbb{E}}t\lbrack\dfrac{\pi\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat{A}_t\rbrack=\hat{\mathbb{E}}_t[r_t(\theta)\hat{A}_t] $$ By doing that we’ll ensure that not having too large policy update because the new policy can’t be too different from the older one.
To do that we have two solutions:
- TRPO (Trust Region Policy Optimization) uses KL divergence constraints outside of the objective function to constraint the policy update. But this method is much complicated to implement and it takes more computation time.
- PPO clip probability ratio directly in the objective function with its Clipped surrogate objective function.
The final Clipped Surrogate(代理) Objective Loss:
# PPO1 + PPO2 连续动作空间
class Skylark_PPO():
def __init__(self, env, gamma = 0.9, epsilon = 0.1, kl_target = 0.01, t='ppo2'):
self.t = t
self.log = 'model/{}_log'.format(t)
self.env = env
self.bound = self.env.action_space.high[0]
self.gamma = gamma
self.A_LR = 0.0001
self.C_LR = 0.0002
self.A_UPDATE_STEPS = 10
self.C_UPDATE_STEPS = 10
# KL penalty, d_target、β for ppo1
self.kl_target = kl_target
self.beta = 0.5
# ε for ppo2
self.epsilon = epsilon
self.sess = tf.Session()
self.build_model()
def _build_critic(self):
"""critic model.
"""
with tf.variable_scope('critic'):
x = tf.layers.dense(self.states, 100, tf.nn.relu)
self.v = tf.layers.dense(x, 1)
self.advantage = self.dr - self.v
def _build_actor(self, name, trainable):
"""actor model.
"""
with tf.variable_scope(name):
x = tf.layers.dense(self.states, 100, tf.nn.relu, trainable=trainable)
mu = self.bound * tf.layers.dense(x, 1, tf.nn.tanh, trainable=trainable)
sigma = tf.layers.dense(x, 1, tf.nn.softplus, trainable=trainable)
norm_dist = tf.distributions.Normal(loc=mu, scale=sigma)
params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=name)
return norm_dist, params
def build_model(self):
"""build model with ppo loss.
"""
# inputs
self.states = tf.placeholder(tf.float32, [None, 3], 'states')
self.action = tf.placeholder(tf.float32, [None, 1], 'action')
self.adv = tf.placeholder(tf.float32, [None, 1], 'advantage')
self.dr = tf.placeholder(tf.float32, [None, 1], 'discounted_r')
# build model
self._build_critic()
nd, pi_params = self._build_actor('actor', trainable=True)
old_nd, oldpi_params = self._build_actor('old_actor', trainable=False)
# define ppo loss
with tf.variable_scope('loss'):
# critic loss
self.closs = tf.reduce_mean(tf.square(self.advantage))
# actor loss
with tf.variable_scope('surrogate'):
ratio = tf.exp(nd.log_prob(self.action) - old_nd.log_prob(self.action))
surr = ratio * self.adv
if self.t == 'ppo1':
self.tflam = tf.placeholder(tf.float32, None, 'lambda')
kl = tf.distributions.kl_divergence(old_nd, nd)
self.kl_mean = tf.reduce_mean(kl)
self.aloss = -(tf.reduce_mean(surr - self.tflam * kl))
else:
self.aloss = -tf.reduce_mean(tf.minimum(
surr,
tf.clip_by_value(ratio, 1.- self.epsilon, 1.+ self.epsilon) * self.adv))
# define Optimizer
with tf.variable_scope('optimize'):
self.ctrain_op = tf.train.AdamOptimizer(self.C_LR).minimize(self.closs)
self.atrain_op = tf.train.AdamOptimizer(self.A_LR).minimize(self.aloss)
with tf.variable_scope('sample_action'):
self.sample_op = tf.squeeze(nd.sample(1), axis=0)
# update old actor
with tf.variable_scope('update_old_actor'):
self.update_old_actor = [oldp.assign(p) for p, oldp in zip(pi_params, oldpi_params)]
tf.summary.FileWriter(self.log, self.sess.graph)
self.sess.run(tf.global_variables_initializer())
def choose_action(self, state):
"""choice continuous action from normal distributions.
Arguments:
state: state.
Returns:
action.
"""
state = state[np.newaxis, :]
action = self.sess.run(self.sample_op, {self.states: state})[0]
return np.clip(action, -self.bound, self.bound)
def get_value(self, state):
"""get q value.
Arguments:
state: state.
Returns:
q_value.
"""
if state.ndim < 2: state = state[np.newaxis, :]
return self.sess.run(self.v, {self.states: state})
def discount_reward(self, states, rewards, next_observation):
"""Compute target value.
Arguments:
states: state in episode.
rewards: reward in episode.
next_observation: state of last action.
Returns:
targets: q targets.
"""
s = np.vstack([states, next_observation.reshape(-1, 3)])
q_values = self.get_value(s).flatten()
targets = rewards + self.gamma * q_values[1:]
targets = targets.reshape(-1, 1)
return targets
def learn(self, states, action, dr):
"""update model.
Arguments:
states: states.
action: action of states.
dr: discount reward of action.
"""
self.sess.run(self.update_old_actor)
adv = self.sess.run(self.advantage,
{self.states: states,
self.dr: dr})
# update actor
if self.t == 'ppo1':
# run ppo1 loss
for _ in range(self.A_UPDATE_STEPS):
_, kl = self.sess.run(
[self.atrain_op, self.kl_mean],
{self.states: states,
self.action: action,
self.adv: adv,
self.tflam: self.beta})
if kl < self.kl_target / 1.5:
self.beta /= 2
elif kl > self.kl_target * 1.5:
self.beta *= 2
else:
# run ppo2 loss
for _ in range(self.A_UPDATE_STEPS):
self.sess.run(self.atrain_op,
{self.states: states,
self.action: action,
self.adv: adv})
# update critic
for _ in range(self.C_UPDATE_STEPS):
self.sess.run(self.ctrain_op,
{self.states: states,
self.dr: dr})
def train(self, num_episodes, batch_size=32, num_steps = 1000):
tf.reset_default_graph()
for i in range(num_episodes):
state = self.env.reset()
states, actions, rewards = [], [], []
steps, sum_rew = 0, 0
done = False
while not done and steps < num_steps:
action = self.choose_action(state)
next_state, reward, done, _ = self.env.step(action)
states.append(state)
actions.append(action)
sum_rew += reward
rewards.append((reward + 8) / 8)
state = next_state
steps += 1
if steps % batch_size == 0:
states = np.array(states)
actions = np.array(actions)
rewards = np.array(rewards)
d_reward = self.discount_reward(states, rewards, next_state)
self.learn(states, actions, d_reward)
states, actions, rewards = [], [], []
print('Episode: {} | Avg_reward: {} | Length: {}'.format(i, sum_rew/steps, steps))
print("Training finished.")
Advantage
It can be used in both discrete and continuous control.
Disadvantage
on-policy -> data inefficient (there is a off-policy version)