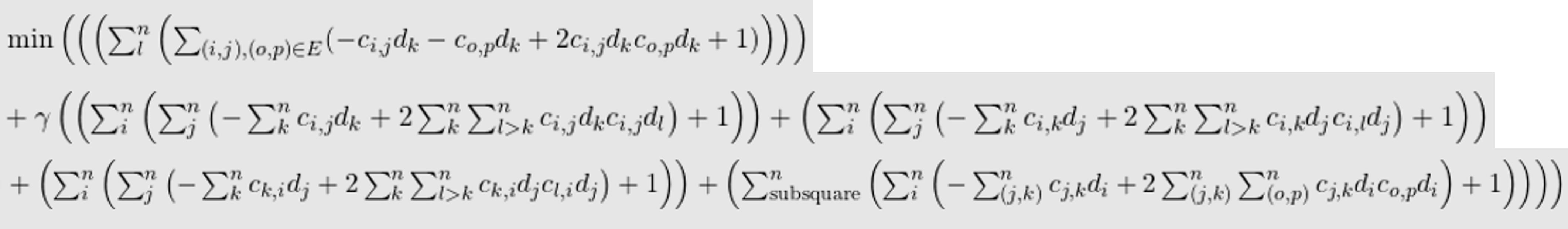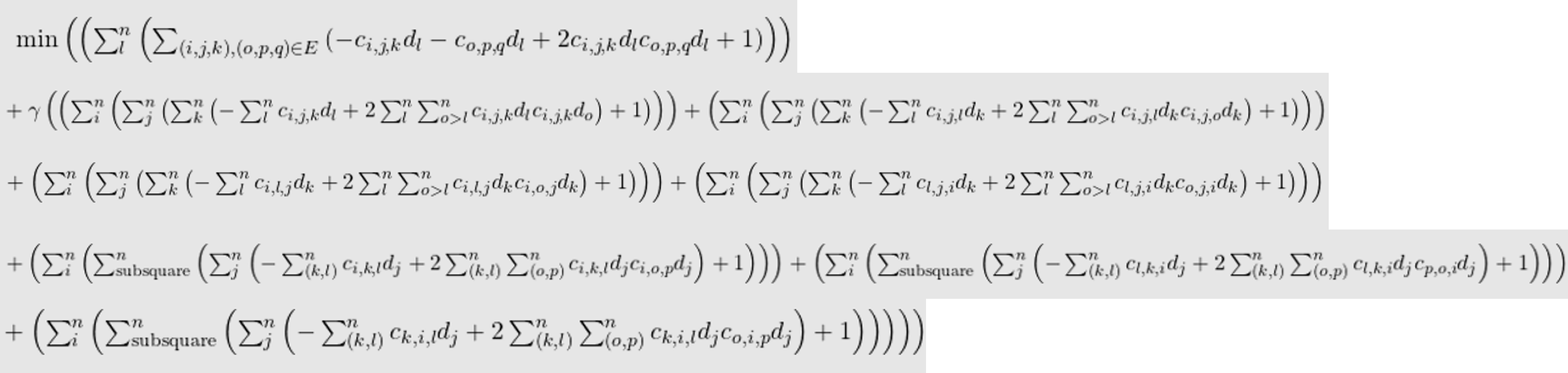solves both 2D and 3D sudoku puzzles using quantum annealing based on the QUBO model
I have designed a quantum sudoku solver that can solve both 2D and 3D sudoku puzzles using the programming language of python along with Dwave’s Ocean sdk. This was implemented in the remaining 3 weeks of my Quantum Computing course.
My solver is successfully able to solve 2D and 3D Sudoku puzzles of varying size and difficulty using the approach of quantum annealing, a branch of quantum computing in which a quantum system attempts to solve a BQM by finding the lowest energy state.
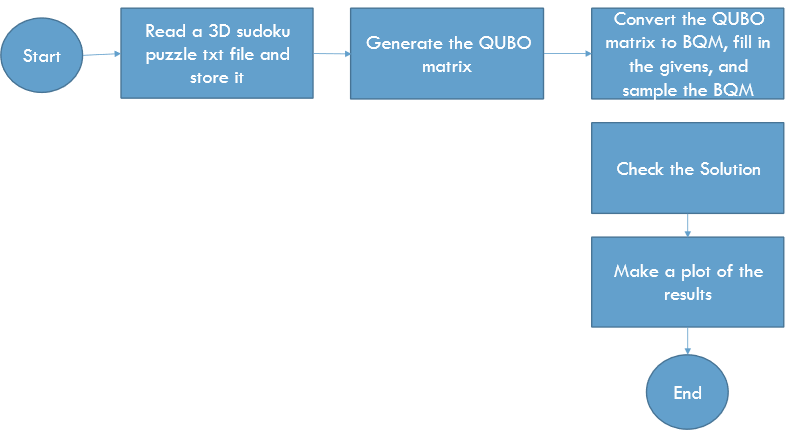
My approach to implementing the quantum sudoku solver involved formulating Quadratic Unconstrained Binary Optimization equations for both 2-dimensional and 3-dimensional Sudoku puzzles and using the equations to write a program which can generate QUBO matrices based on arbitrary Sudoku puzzles. The QUBO matrix would then be converted into a BQM to be inputted into the sampler to obtain a solution. As an additional feature, I utilized matplotlib to generate plots of solutions to assist with the visualization of the results.
In my equations, each variable is represented by a pair of c and d letters. c represents a particular cell of the sudoku puzzle using two coordinate indices, and d represents the particular digit being used out of the n possible digits. I group these two properties as one variable in order to allow me to differentiate which part of the variable represents the cell and which part represents the digit. The indices i, j, and k represent the order in which the values will be cycled through. Generally, the index that is cycled through first is the one that is enclosed by the innermost parentheses and so on.
My equations for the 3D sudoku solver are similar to those of the 2D sudoku. However, for these equations, there is one more index as a consequence of the additional dimension. So, we now have indices i, j, k, and l.
Each variable is represented by a pair of c and d letters. c represents a particular cell of the sudoku puzzle using three coordinate indices, and d represents the particular digit being used out of the n possible digits.
The program I have written for my Sudoku solver can be divided into two parts: the nxn Sudoku solver (2D) and the nxnxn Sudoku solver (3D). There are 4 python files associated with each solver.
For the nxn sudoku solver, there are the nxn_generate.py, nxn_plot.py, nxn_QUBO.py, and nxn_solver.py files.
Similarly, for the nxnxn sudoku solver, there are the nxnxn_generate.py, nxnxn_plot.py, nxnxn_QUBO.py, and nxnxn_solver.py files.
This python file is used for generating Sudoku puzzles of arbitrary size, and the user can specify the number of empty cells that should initially be on the Sudoku puzzle. The nxn_generate.py file generates 2D nxn sudoku puzzles and the nxnxn_generate.py file generates 3D nxnxn sudoku puzzles by generating n sudoku layers that would form the nxnxn cube.
I did not come up with this sudoku generator completely by myself. Credit for this part of the program goes to Emma Hogan (https://github.com/roonil-wazlib/3D_Sudoku). I only had to make small modifications to their program in order to generate puzzles of arbitrary size. This was really convenient because it allowed me to efficiently test my program on various sizes and difficulties of sudoku puzzles without having to manually copy puzzles from different internet sites.
This python file is used for generating nice-looking visuals of the results obtained by my solver. It actually plots the solution onto a sudoku grid using matplotlib, which is really convenient for reading larger sudoku puzzles. The nxn_plot.py file just plots the result onto an nxn sudoku grid, and the nxnxn_plot.py file actually creates a visualization of the cube with the numbers filled in and then it proceeds to display the 3n nxn sudoku layers, which make up the nxnxn cube, onto nxn sudoku grids.
This python file is used for generating the QUBO matrices needed for solving the sudoku puzzles. These files are based on the QUBO equations. Within these files, there is actually two options for generating a QUBO matrix: the simple QUBO generator and the complex QUBO generator. The simple QUBO only takes into account the constraint parts of the QUBO equations I formulated, and the complex QUBO will take into account both the objective and constraint parts of the QUBO equations I formulated. I did this because I was initially unsure of the effectiveness of the objective function on the full QUBO equation, so I created these two options to allow me to quickly switch between the two versions of the QUBO equations.
This python file acts kind of like a main file for each version of sudoku. Within this file, the conversion of the QUBO matrix into a BQM occurs as well as the sampling of the BQM to obtain the final results. Additionally, I added some functions into these files which enable the program to determine if the solution found is correct and to print the results onto the screen in plaint text.
This python file acts as the main controller for the entire program. It has access to all the other files and the user can generate and solve sudoku puzzles of 2D or 3D type directly from this file.
Looking into the directory of the program, you will see that there are various .txt files of varying names, such as “9x9.txt” or “9x9x9.txt”. These are actually the files that store the generated example puzzles which the solver attempts to solve. If it is in the “nxn.txt” format, then it is a 2D puzzle, and similarly the “nxnxn.txt” format means that it is a 3D puzzle.
It can solve puzzles of sizes 4x4-25x25
It can solve puzzles of sizes 4x4x4-25x25x25. Possibly more, but I have not tried yet.
You need python 3, Dwave Ocean sdk, and matplotlib
Run the program on a terminal
You just run the sudoku_main.py file and provide two additional arguements. One is to specify if you want to solve or generate a sudoku puzzle, and the other is to specify the puzzle you want to solve or generate. Make sure to only use "solve" or "generate" for the first argument, and "nxn" or "nxnxn" format for the second argument.
Also, make sure the n you choose is an integer such that its square root is also an integer, otherwise the program won't work because it only solves the most conventional sizes.
(ocean) C:\Users\mario\PycharmProjects\QuantumSudokuFinal>python sudoku_main.py solve 4x4x4
or
(ocean) C:\Users\mario\PycharmProjects\QuantumSudokuFinal>python sudoku_main.py generate 4x4x4
You have to specify which QUBO generator you want to use. Complex QUBO includes a graph coloring application in the equations, and simple QUBO does not.
Then you must specify if you want to make a plot (1 for yes, 0 for no) and the number of samples.
QUBO Type? (1 for complex, 0 for simple): 1
Make Plot? (1 for yes, 0 for no): 1
How many samples?: 5
Just specify the number of blanks you want the puzzle to have. It tells you the maximum number of blanks the puzzle can have, so don't go over that number.
Number of Blanks (max is 64):63
The sampler is set to the "neal" simulated annealer by default, but it can be changed by modifying the sudoku_main.py file.