-
Notifications
You must be signed in to change notification settings - Fork 0
JWormBench Design
The idea behind WormBench is inspired in the Snake game. In this case the snakes are worms formed by a body and head, moving in a shared world - matrix of nodes. Each node has an integer value and the worms' group id that is over that node (worms belonging to other groups should not cross through each other).
The total sum of the values of all world's nodes is the world's state. For read-only workloads, the world's state should remain unchanged by the execution of the benchmark.
A worm object has the following properties: unique identifier, group id, speed, head's size, coordinates of the head, and coordinates of the body. A worm provides a move method that receives a direction as parameter and moves the worm. Moving the worm includes two tasks: (1) updates the coordinates of the body according to the new direction and (2) updates the nodes below the body with the worm's reference.
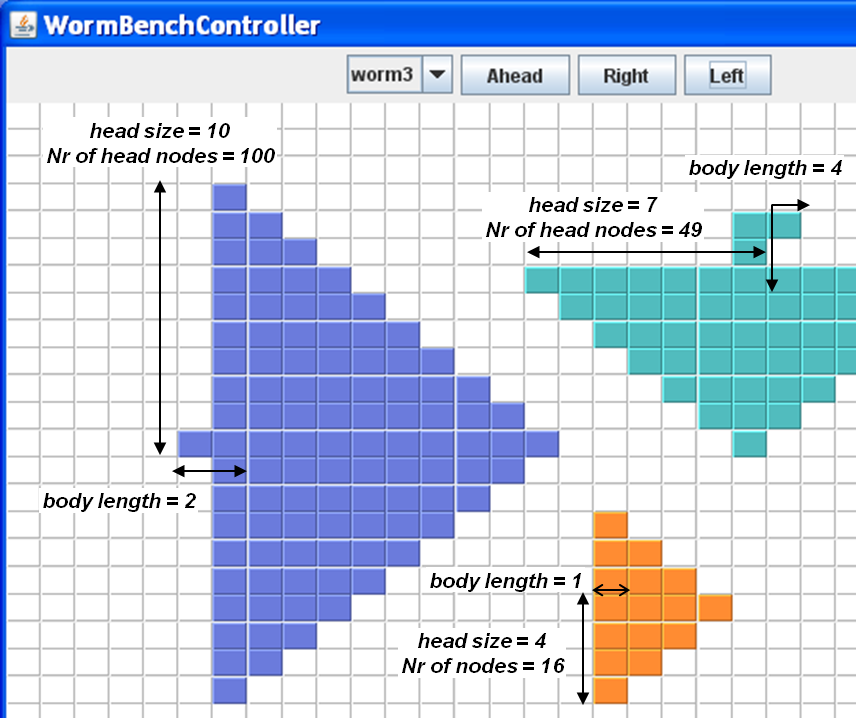
The worms perform worm operations on the nodes under the worms's head. The number of nodes under the head of the worm is equal to the square of his head's size, as illustrated in the following figure. Given that a worm reads all the nodes under its head for each worm operation and a transaction performs just one worm operation, this means that the length of the transaction read-set grows quadratically with the head's size of the worm.
One of the key differences from WormBench is the STM integration model of JWormBench. For that purpose, the JWormBench introduces the concept of step that is an abstraction of an iteration performed by the worm's thread. A step includes the following tasks: (1) performs a worm operation, (2) moves the worm, updating the coordinates of the body and the head of the worm, and (3) updates the nodes under the body with the worm's reference.
The JWormBench implementation provides 13 types of worm operations, which are presented in the following Table:
#| Operation | read-set | write-set | complexity | ----|-------------|-------------|-------------|-------------|------------- 0 | Sum |head's size^2| 0 | O(n) | returns the sum of the nodes' values under the worm's head 1 | Average |head's size^2 | 0 | O(n) | returns the average of the nodes' values under the worm's head 2 | Median |head's size^2 | 0 | O(n2) | returns the median value of the nodes under the worm's head 3 | Minimum |head's size^2 | 0 | O(n) | returns the minimum value of the nodes under the worm's head 4 | Maximum |head's size^2 | 0 | O(n) | returns the maximum value of the nodes under the worm's head 5 | ReplaceMaxWithAverage |2 * head's size^2 | 1 | O(n) | replaces the maximum by the average of the nodes' values under the worm's head 6 | ReplaceMinWithAverage |2 * head's size^2 | 1 | O(n) | replaces the minimum by the average of the nodes' values under the worm's head 7 | ReplaceMedianWithAverage |2 * head's size^2 | 1 | O(n2) | replaces the median by the average of the nodes' values under the worm's head 8 | ReplaceMedianWithMax |2 * head's size^2 | 1 | O(n2) | replaces the median by the maximum value of the nodes under the worm's head 9 | ReplaceMedianWithMin |2 * head's size^2 | 1 | O(n2) | replaces the median by the minimum value of the nodes under the worm's head 10 | ReplaceMaxWithMin |2 * head's size^2 | 1 | O(n) | replaces the maximum by the minimum value of the nodes under the worm's head 11 | Sort |head's size^2 |head's size^2 | O(n2) | sort the values of the nodes under worm's head and write them back to those nodes 12 | Transpose |head's size^2 |head's size^2 | O(n) | transpose the values of the nodes under worm's head and write them back to those nodes
These operations may be grouped in three categories:
- read-only - Sum, Average, Median, Minimum, and Maximum (from #0 to #4). Each of these operations reads all the nodes under the worm's head, corresponding to head's size^2_ nodes;
- n-reads-1-write - ReplaceWith (from #5 to #10). Each of these operations combines two of the read-only operations described in the previous item: They use the value returned by the first operation to update the node returned by the second. Each operation makes 2*head's size^2_ reads and one write, updating the world's state.
- n-reads-n-writes - Sort (#11) and Transpose (#12). When these operations are properly synchronized with other concurrent worm operations, they preserve the world's state, i.e. the total value of all nodes in the world remains the same before and after the execution of these operations.
The JWormBench’s world is accessed by worms that can update the nodes’ values. If we use a read-only workload and the nodes’ values are not modified by worms, then the world’s state must be the same before and after workload execution.
On the other hand, for read-write workloads the total value can change, or not, depending on the kind of update operations. For instance, if we just use operations of n-reads-n-writes category as sort and transpose (see table above), the world’s state will be preserved.
But for operations of n-reads-1-writes like ReplaceWith, then the total value of world nodes will change. To verify if the total value is correct at the end of work-load execution, we must store in the thread’s private buffer the difference between the new and the old value updated by a worm operation. At the end subtracting the accumulated differences on each thread’s private buffer to the total value of all nodes, must be equals to the initial sum of nodes’ values.