This package estimates linear models with high dimensional categorical variables and/or instrumental variables.

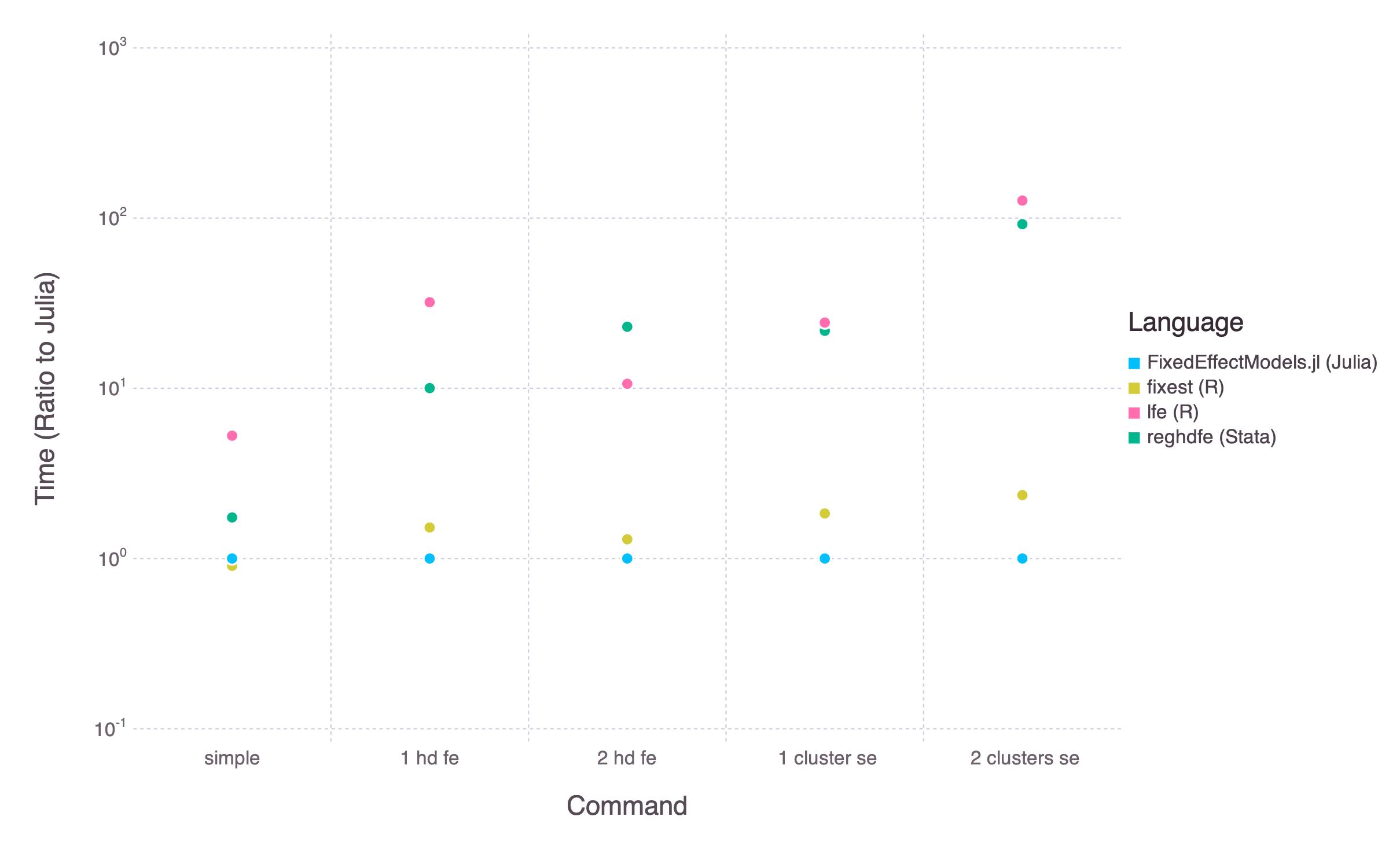
Its objective is similar to the Stata command reghdfe and the R function felm. The package tends to be much faster than these two options.

Installation

The package is registered in the General registry and so can be installed at the REPL with ] add FixedEffectModels.

Syntax

using DataFrames, RDatasets, FixedEffectModels
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), Vcov.cluster(:State), weights = :Pop)
# =====================================================================
# Number of obs:               1380   Degrees of freedom:            31
# R2:                         0.804   R2 within:                  0.139
# F-Statistic:              13.3481   p-value:                    0.000
# Iterations:                     6   Converged:                   true
# =====================================================================
#         Estimate  Std.Error  t value Pr(>|t|)   Lower 95%   Upper 95%
# ---------------------------------------------------------------------
# NDI  -0.00526264 0.00144043 -3.65351    0.000 -0.00808837 -0.00243691
# =====================================================================

• A typical formula is composed of one dependent variable, exogeneous variables, endogeneous variables, instrumental variables, and a set of high-dimensional fixed effects.

  dependent variable ~ exogenous variables + (endogenous variables ~ instrumental variables) + fe(fixedeffect variable)

  High-dimensional fixed effect variables are indicated with the function fe. You can add an arbitrary number of high dimensional fixed effects, separated with +. Moreover, you can interact a fixed effect with a continuous variable (e.g. fe(State)&Year) or with another fixed effect (e.g. fe(State)&fe(Year)).

  reg(df, @formula(Sales ~ Price + fe(State) + fe(Year)))
  reg(df, @formula(Sales ~ NDI + fe(State) + fe(State)&Year))
  reg(df, @formula(Sales ~ NDI + fe(State)&fe(Year)))
  reg(df, @formula(Sales ~ (Price ~ Pimin)))

  To construct formula programatically, use

  reg(df, Term(:Sales) ~ Term(:NDI) + fe(Term(:State)) + fe(Term(:Year))

• Standard errors are indicated with the prefix Vcov.

   Vcov.robust()
   Vcov.cluster(:State)
   Vcov.cluster(:State, :Year)

• The option weights specifies a variable for weights

   weights = :Pop

• The option subset specifies a subset of the data

   subset = df.State .>= 30

• The option save can be set to one of the following: :residuals to save residuals, :fe to save fixed effects, true to save both

• The option method can be set to one of the following: :lsmr, :lsmr_gpu, :lsmr_threads, :lsmr_cores (see Performances below).

• The option contrasts specifies particular contrasts for categorical variables in the formula, e.g.

   df.YearC = categorical(df.Year)
   reg(df, @formula(Sales ~ YearC); contrasts = Dict(:YearC => DummyCoding(base = 80)))

Output

reg returns a light object. It is composed of

• the vector of coefficients & the covariance matrix (use coef, coefnames, vcov on the output of reg)
• a boolean vector reporting rows used in the estimation
• a set of scalars (number of observations, the degree of freedoms, r2, etc)
• with the option save = true, a dataframe aligned with the initial dataframe with residuals and, if the model contains high dimensional fixed effects, fixed effects estimates (use residuals or fe on the output of reg)

Methods such as predict, residuals are still defined but require to specify a dataframe as a second argument. The problematic size of lm and glm models in R or Julia is discussed here, here, here here (and for absurd consequences, here and there).

You may use RegressionTables.jl to get publication-quality regression tables.

Performances

GPU

The package has support for GPUs (Nvidia) (thanks to Paul Schrimpf). This can make the package an order of magnitude faster for complicated problems.

First make sure that using CuArrays works without issue. Then, estimate a model with method = :lsmr_gpu.

When working on the GPU, it is encouraged to set the floating point precision to Float32 with double_precision = false, since it is usually much faster.

using FixedEffectModels
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), method = :lsmr_gpu, double_precision = false)

Parallel Computing

The package has support for multi-threading and multi-cores. In this case, each regressor is demeaned in a different thread. It only allows for a modest speedup (between 10% and 60%) since the demeaning operation is typically memory bound.

# Multi-threading
Threads.nthreads()
using DataFrames, RDatasets, FixedEffectModels
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), method = :lsmr_threads)

# Multi-cores 
using Distributed
addprocs(4)
@everywhere using DataFrames,  RDatasets, FixedEffectModels
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), method = :lsmr_cores)

Solution Method

Denote the model y = X β + D θ + e where X is a matrix with few columns and D is the design matrix from categorical variables. Estimates for β, along with their standard errors, are obtained in two steps:

1. y, X are regressed on D using the package FixedEffects.jl
2. Estimates for β, along with their standard errors, are obtained by regressing the projected y on the projected X (an application of the Frisch Waugh-Lovell Theorem)
3. With the option save = true, estimates for the high dimensional fixed effects are obtained after regressing the residuals of the full model minus the residuals of the partialed out models on D using the package FixedEffects.jl

References

Baum, C. and Schaffer, M. (2013) AVAR: Stata module to perform asymptotic covariance estimation for iid and non-iid data robust to heteroskedasticity, autocorrelation, 1- and 2-way clustering, and common cross-panel autocorrelated disturbances. Statistical Software Components, Boston College Department of Economics.

Correia, S. (2014) REGHDFE: Stata module to perform linear or instrumental-variable regression absorbing any number of high-dimensional fixed effects. Statistical Software Components, Boston College Department of Economics.

Fong, DC. and Saunders, M. (2011) LSMR: An Iterative Algorithm for Sparse Least-Squares Problems. SIAM Journal on Scientific Computing

Gaure, S. (2013) OLS with Multiple High Dimensional Category Variables. Computational Statistics and Data Analysis

Kleibergen, F, and Paap, R. (2006) Generalized reduced rank tests using the singular value decomposition. Journal of econometrics

Kleibergen, F. and Schaffer, M. (2007) RANKTEST: Stata module to test the rank of a matrix using the Kleibergen-Paap rk statistic. Statistical Software Components, Boston College Department of Economics.