Adding H-Entropy Search and a corresponding tutorial (#1794)

Summary:
<!--
Thank you for sending the PR! We appreciate you spending the time to make BoTorch better.

Help us understand your motivation by explaining why you decided to make this change.

You can learn more about contributing to BoTorch here: https://github.com/pytorch/botorch/blob/main/CONTRIBUTING.md
-->

## Motivation

This pull request introduces an implementation of the H-Entropy Search [1] procedure, along with a tutorial covering two tasks: Top-K Search and MinMax Search. This PR addresses issue #1733, which requested a new acquisition function for top-K search.
[1] W. Neiswanger, L. Yu, S. Zhao, C. Meng, S. Ermon. Generalizing Bayesian Optimization with Decision-theoretic Entropies. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022).

### Have you read the [Contributing Guidelines on pull requests](https://github.com/pytorch/botorch/blob/main/CONTRIBUTING.md#pull-requests)?

Yes, I have read the Contributing Guidelines on pull requests.

Pull Request resolved: #1794

Test Plan:
(Write your test plan here. If you changed any code, please provide us with clear instructions on how you verified your changes work. Bonus points for screenshots and videos!)

In the associated tutorial, two tests can be executed using the built-in 2D Ackley function with an input range of [-1, 1]. Within this range, there are four maxima located at each corner and one minimum at the center. The H-Entropy Search (HES) procedure, employing a Top-K (K = 2) loss function, is expected to identify two of the four maxima, with any combination being acceptable. Meanwhile, the H-Entropy Search procedure utilizing the MinMax loss function should locate one maximum and the central minimum.

Below are the results after running 10 steps of HES with MinMax: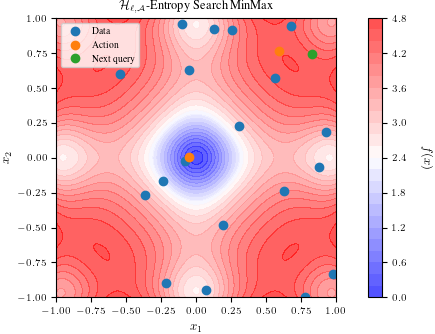
![image](https://user-images.githubusercontent.com/45890770/232338473-b55c96f1-8710-4496-8d8f-15215889e818.png)

And here are the results after running 10 steps of HES with TopK: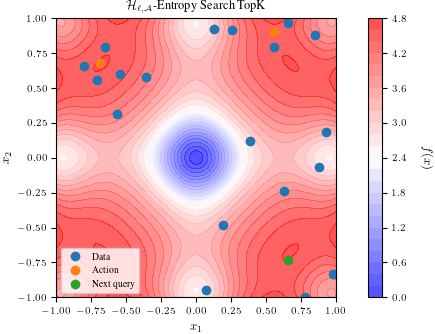
![image](https://user-images.githubusercontent.com/45890770/232338763-0a142d74-96ff-4e4f-a364-92937087fec7.png)

Both images can be reproduced by following the respective tutorial.

## Related PRs

Not applicable.

(If this PR adds or changes functionality, please take some time to update the docs at https://github.com/pytorch/botorch, and link to your PR here.)

Reviewed By: esantorella

Differential Revision: D46999676

Pulled By: saitcakmak

fbshipit-source-id: 4486c7e55919a331ed8bca9e7f2029ac7eeed54a

botorch_community/acquisition/hentropy_search.py

@@ -0,0 +1,257 @@
+#!/usr/bin/env python3
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+#
+# This source code is licensed under the MIT license found in the
+# LICENSE file in the root directory of this source tree.
+
+r"""
+This file has an implementation of Batch H-Entropy Search (qHES) via
+one-shot optimization as introduced in [Neiswanger2022]_.
+
+The authors adopt a generalized definition of entropy from past work
+in Bayesian decision theory, which proposes a family of decision-theoretic
+entropies parameterized by a problem-specific loss function and
+action set. The each action is typically a set of points in the input
+space which represents what we would like to do after gathering information
+about the blackbox function. The method allow the development of a common
+acquisition optimization procedure, which applies generically
+to many members of this family (where each member is induced by a
+specific loss function and action set).
+
+.. [Neiswanger2022]
+    W. Neiswanger, L. Yu, S. Zhao, C. Meng, S. Ermon. Generalizing Bayesian
+    Optimization with Decision-theoretic Entropies. Appears in Proceedings
+    of the 36th Conference on Neural Information Processing Systems
+    (NeurIPS 2022)
+
+Contributor: sangttruong, martinakaduc
+"""
+
+from __future__ import annotations
+
+from typing import Any, Dict, Optional, Tuple
+
+import torch
+import torch.nn as nn
+from botorch.acquisition.acquisition import OneShotAcquisitionFunction
+from botorch.acquisition.monte_carlo import MCAcquisitionFunction
+from botorch.models.model import Model
+from botorch.sampling.base import MCSampler
+from botorch.sampling.normal import SobolQMCNormalSampler
+from botorch.utils.transforms import t_batch_mode_transform
+from torch import Tensor
+
+
+def get_sampler_and_num_points(
+    sampler: Optional[MCSampler],
+    num_points: Optional[int],
+) -> Tuple[MCSampler, int]:
+    r"""Make sure the sampler and num_points are consistent, if specified.
+    If the sampler is not specified, construct one.
+    """
+    if sampler is None:
+        if num_points is None:
+            raise ValueError("Must specify `num_points` if no `sampler` is provided.")
+        sampler = SobolQMCNormalSampler(sample_shape=torch.Size([num_points]))
+    elif num_points is not None and sampler.sample_shape[0] != num_points:
+        raise ValueError(f"The sample shape of the sampler must match {num_points=}.")
+    else:
+        num_points = sampler.sample_shape[0]
+    return sampler, num_points
+
+
+class qHEntropySearch(MCAcquisitionFunction, OneShotAcquisitionFunction):
+    r"""H-Entropy Search using one-shot optimization."""
+
+    def __init__(
+        self,
+        model: Model,
+        loss_function_class: nn.Module,
+        loss_function_hyperparameters: Dict[str, Any],
+        n_fantasy_at_design_pts: Optional[int] = 64,
+        n_fantasy_at_action_pts: Optional[int] = 64,
+        design_sampler: Optional[MCSampler] = None,
+        action_sampler: Optional[MCSampler] = None,
+    ) -> None:
+        r"""Batch H-Entropy Search using one-shot optimization.
+
+        Args:
+            model: A fitted model. Must support fantasizing.
+            loss_function_class: The loss function class that is used to compute
+                the expected loss of the fantasized actions.
+            loss_function_hyperparameters: The hyperparameters for the loss
+                function class.
+            n_fantasy_at_design_pts: Number of fantasized outcomes for each
+                design point. Must match the sample shape of `design_sampler`
+                if specified.
+            n_fantasy_at_action_pts: Number of fantasized outcomes for each
+                action point. Must match the sample shape of `action_sampler`
+                if specified.
+            design_sampler: The sampler used to sample fantasized outcomes at each
+                design point. Optional if `n_fantasy_at_design_pts` is specified.
+            action_sampler: The sampler used to sample fantasized outcomes at each
+                action point. Optional if `n_fantasy_at_design_pts` is specified.
+        """
+
+        super(MCAcquisitionFunction, self).__init__(model=model)
+
+        self.design_sampler, self.n_fantasy_at_design_pts = get_sampler_and_num_points(
+            sampler=design_sampler, num_points=n_fantasy_at_design_pts
+        )
+        self.action_sampler, self.n_fantasy_at_action_pts = get_sampler_and_num_points(
+            sampler=action_sampler, num_points=n_fantasy_at_action_pts
+        )
+        self.loss_function_hyperparameters = loss_function_hyperparameters
+        self.loss_function = loss_function_class(
+            **self.loss_function_hyperparameters,
+        )
+
+    @t_batch_mode_transform()
+    def forward(self, X: Tensor, A: Tensor) -> Tensor:
+        r"""Evaluate qHEntropySearch objective (q-HES) on the candidate set `X`.
+
+        Args:
+            X: Design tensor of shape `(batch) x q x design_dim`.
+            A: Action tensor of shape `(batch) x n_fantasy_at_design_pts
+                x num_actions x action_dim`.
+
+        Returns:
+            A Tensor of shape `(batch)`.
+        """
+
+        # construct the fantasy model of shape `n_fantasy_at_design_pts x b`
+        fantasy_model = self.model.fantasize(X=X, sampler=self.design_sampler)
+
+        # Permute shape of A to work with self.model.posterior correctly
+        A = A.permute(1, 0, 2, 3)
+
+        fantasized_outcome = self.action_sampler(fantasy_model.posterior(A))
+        # >>> n_fantasy_at_action_pts x n_fantasy_at_design_pts
+        # ... x batch_size x num_actions x 1
+
+        fantasized_outcome = fantasized_outcome.squeeze(dim=-1)
+        # >>> n_fantasy_at_action_pts x n_fantasy_at_design_pts
+        # ... x batch_size x num_actions
+
+        values = self.loss_function(A=A, Y=fantasized_outcome)
+        # >>> n_fantasy_at_design_pts x batch_size
+
+        # return average over the fantasy samples
+        return values.mean(dim=0)
+
+    def get_augmented_q_batch_size(self, q: int) -> int:
+        r"""Get augmented q batch size for optimization.
+
+        Args:
+            q: The number of candidates to consider jointly.
+
+        Returns:
+            The augmented size for optimization.
+        """
+
+        return q + self.n_fantasy_at_design_pts
+
+    def extract_candidates(self, X_full: Tensor) -> Tensor:
+        r"""We only return X as the set of candidates post-optimization.
+
+        Args:
+            X_full: A `b x (q + num_fantasies) x d`-dim Tensor with `b`
+                t-batches of `q + num_fantasies` design points each.
+
+        Returns:
+            A `b x q x d`-dim Tensor with `b` t-batches of `q` design points each.
+        """
+        return X_full[..., : -self.n_fantasy_at_design_pts, :]
+
+
+class qLossFunctionTopK(nn.Module):
+    r"""Batch loss function for the task of finding top-K
+    relative to the values of the objective function."""
+
+    def __init__(self, dist_weight=1.0, dist_threshold=0.5) -> None:
+        r"""Batch loss function for the task of finding top-K
+        relative to the values of the objective function.
+
+        Args:
+            dist_weight: The weight of the distance between actions in the
+                loss function.
+            dist_threshold: The threshold for the distance between actions.
+        """
+
+        super().__init__()
+        self.dist_weight = dist_weight
+        self.dist_threshold = dist_threshold
+
+    def forward(self, A: Tensor, Y: Tensor) -> Tensor:
+        r"""Evaluate batch loss function on a tensor of actions.
+
+        Args:
+            A: Action tensor with shape `n_fantasy_at_design_pts x batch_size
+                x num_actions x action_dim`.
+            Y: Fantasized sample with shape `n_fantasy_at_action_pts x
+                n_fantasy_at_design_pts x batch_size x num_actions`.
+
+        Returns:
+            A Tensor of shape `n_fantasy_at_action_pts x batch_size`.
+        """
+
+        Y = Y.sum(dim=-1).mean(dim=0)
+        # >>> n_fantasy_at_design_pts x batch_size
+
+        num_actions = A.shape[-2]
+
+        dist_reward = 0
+        if num_actions >= 2:
+            A = A.contiguous()
+            # >>> n_fantasy_at_design_pts x batch_size x num_actions x action_dim
+
+            A_distance = torch.cdist(A, A, p=1.0)
+            # >>> n_fantasy_at_design_pts x batch_size x num_actions x num_actions
+
+            A_distance_triu = torch.triu(A_distance)
+            # >>> n_fantasy_at_design_pts x batch_size x num_actions x num_actions
+
+            A_distance_triu[A_distance_triu > self.dist_threshold] = self.dist_threshold
+            # >>> n_fantasy_at_design_pts x batch_size x num_actions x num_actions
+
+            denominator = num_actions * (num_actions - 1) / 2.0
+
+            dist_reward = A_distance_triu.sum((-1, -2)) / denominator
+            # >>> n_fantasy_at_design_pts x batch_size
+
+        q_hes = Y + self.dist_weight * dist_reward
+        # >>> n_fantasy_at_design_pts x batch_size
+
+        return q_hes
+
+
+class qLossFunctionMinMax(nn.Module):
+    r"""Batch loss function for the task of finding min and max
+    relative to the values of the objective function."""
+
+    def __init__(self) -> None:
+        r"""Loss function for task of finding min and max
+        relative to the values of the objective function."""
+
+        super().__init__()
+
+    def forward(self, A: Tensor, Y: Tensor) -> Tensor:
+        r"""Evaluate batch loss function on a tensor of actions.
+
+        Args:
+            A: Action tensor with shape `n_fantasy_at_design_pts x batch_size
+                x num_actions x action_dim`.
+            Y: Fantasized sample with shape `n_fantasy_at_action_pts x
+                n_fantasy_at_design_pts x batch_size x num_actions`.
+
+        Returns:
+            A Tensor of shape `n_fantasy_at_action_pts x batch`.
+        """
+
+        if A.shape[-2] != 2:  # pragma: no cover
+            raise RuntimeError("qLossFunctionMinMax only supports 2 actions.")
+
+        q_hes = (Y[..., 1:].sum(dim=-1) - Y[..., 0]).mean(dim=0)
+        # >>> n_fantasy_at_design_pts x batch_size
+
+        return q_hes