Pharmokinetic Model - NERC DTP Group 1

About

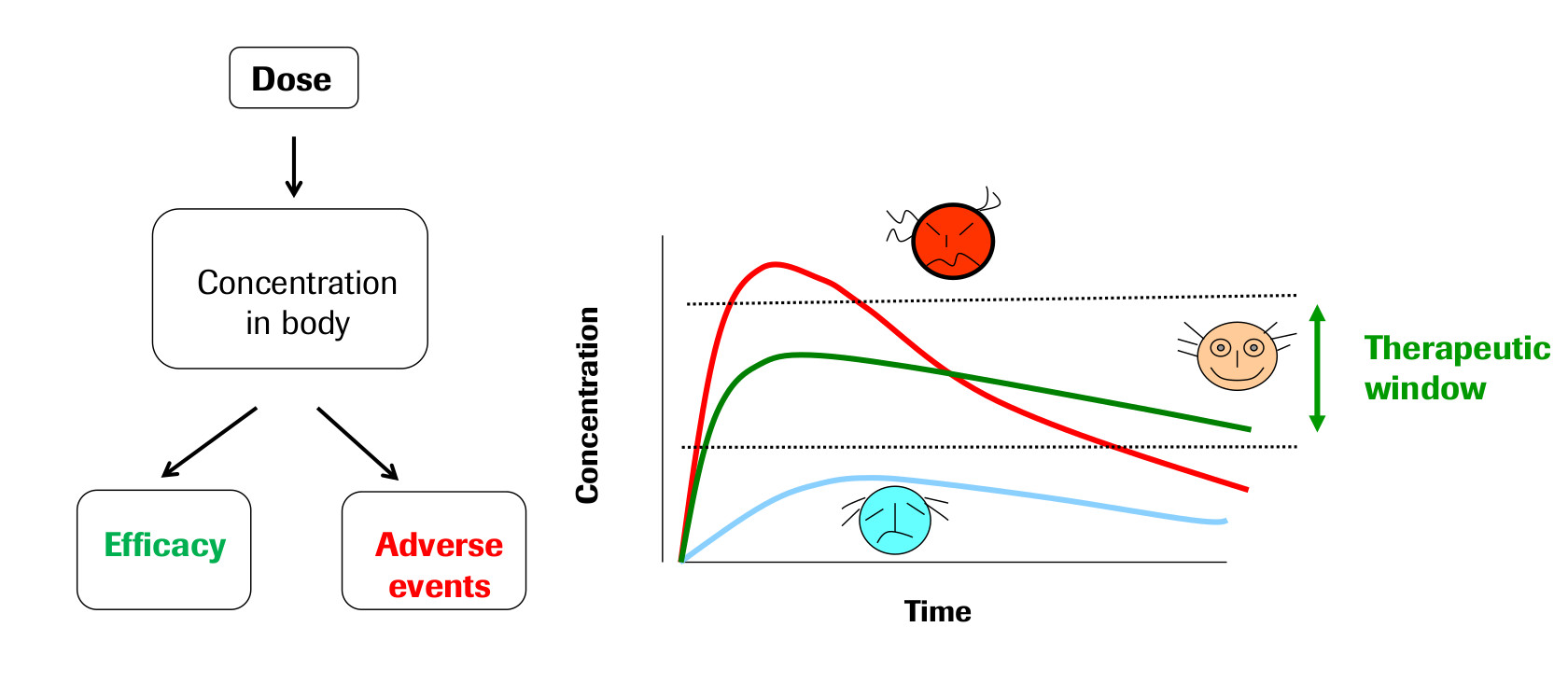
The field of Pharmacokinetics (PK) provides a quantitative basis for describing the delivery of a drug to a patient, the diffusion of that drug through the plasma/body tissue, and the subsequent clearance of the drug from the patient's system. PK is used to ensure that there is sufficient concentration of the drug to maintain the required efficacy of the drug, while ensuring that the concentration levels remain below the toxic threshold (See Fig 1).

There are two PK models that this package solves, Intravenous Bolus Dosing, and Subcutaneous Dosing. The models are described in the following sections.

Intravenous Bolus Dosing Protocol

The following example PK model describes a two-compartment model. The time-dependent variables to be solved are the drug quantity in the central and peripheral compartments, $q_c$ and $q_{p1}$ (units: [ng]) respectively.

$$ \begin{align} \frac{d q_c}{dt} &= \text{Dose}(t) - \frac{q_c}{V_c} CL - Q_{p1}\left( \frac{q_c}{V_c} - \frac{q_{p1}}{V_p1}\right)\\ \frac{d q_1}{dt} &= Q_{p1}\left( \frac{q_c}{V_c} - \frac{q_{p1}}{V_p1}\right) \end{align} $$

Subcutaneous Dosing Protocol

The following example PK model describes a three-compartment model. The time-dependent variables to be solved are the drug quantity in a compartment before the central compartment, the central, and peripheral compartments, $q_0$, $q_c$ and $q_{p1}$ (units: [ng]) respectively. $$ \begin{align} \frac{d q_0}{dt} &= \text{Dose}(t) - k_0 q_0 \ \frac{d q_c}{dt} &= k_0 q_0 - \frac{q_c}{V_c} CL - Q_{p1}\left( \frac{q_c}{V_c} - \frac{q_{p1}}{V_p1}\right)\ \frac{d q_1}{dt} &= Q_{p1}\left( \frac{q_c}{V_c} - \frac{q_{p1}}{V_p1}\right) \end{align} $$

Installation of Model

Installing package for general use

1. Setup virtual environment:
   1. python3 -m venv venv Setup virtual environment
   2. source venv/bin/activate Activate virtual environment
2. Install package:
   1. pip install --index-url https://test.pypi.org/simple --extra-index-url https://pypi.org/simple pkmodel-NERC1 Install package from Test PyPi.

Installing the package for development

1. Download package from GitHub:
   1. git clone [email protected]:robertdoanesolomon/software-engineering-projects-pk.git
   2. cd software-engineering-projects-pk
   3. git checkout --track origin/branch-name Optionally switch branch for development.
2. Setup virtual environment:
   1. python3 -m venv venv Setup virtual environment
   2. source venv/bin/activate Activate virtual environment
3. Install package:
   1. pip install -e . Install package
4. Test
   1. python run_test.py for example on how to call and use model

Example Model Use

After installing the pkmodel package, you can select the dosing protocol, run the model, and save save a visualisation of the results as follows:

Note that:

• the model simulates 1 hour only of drug delivery, calculated with 1000 timesteps,
• the model only simulates continuous, steady state, drug delivery over the one simulated hour, with the dose set in the parameters - see example below,
• this example is also available in run_test.py in the root directory of the package.

import pkmodel

#### Example run of the IV model

# Choose parameters for the model
# params = [Q_p1, V_c, V_p1, CL, X], where X is dose in each time step
params = [1, 1, 1, 1, 1]

# Initalise the model with the parameters
model_to_use = pkmodel.model.IV(parametersIV=params)

# Integrate the model to obtain solution
# The output of model_to_use.integrate() is a numpy array of dimension
# (2, 1000) where 1000 is the number of time steps, and 3 is the number of
# compartments in the order [q_c, q_p1, q_0]
solution = model_to_use.integrate()

# Visualise the solution and save to file
pkmodel.solution.visualise(solution, 'figure_IV.png')


##### Example run of the SC model

# Choose parameters for the model
# params = [Q_p1, V_c, V_p1, CL, X, ka], where X is dose in each time step
params = [1, 1, 1, 1, 1, 1]

# Initalise the model with the parameters
model_to_use = pkmodel.model.SC(parametersSC=params)

# Integrate the model to obtain solution
# The output of model_to_use.integrate() is a numpy array of dimension
# (3, 1000) where 1000 is the number of time steps, and 3 is the number of
# compartments in the order [q_c, q_p1]
solution = model_to_use.integrate()

# Visualise the solution and save to file
pkmodel.solution.visualise(solution, 'figure_SC.png')