Home

Rubikcubisme

Introduction

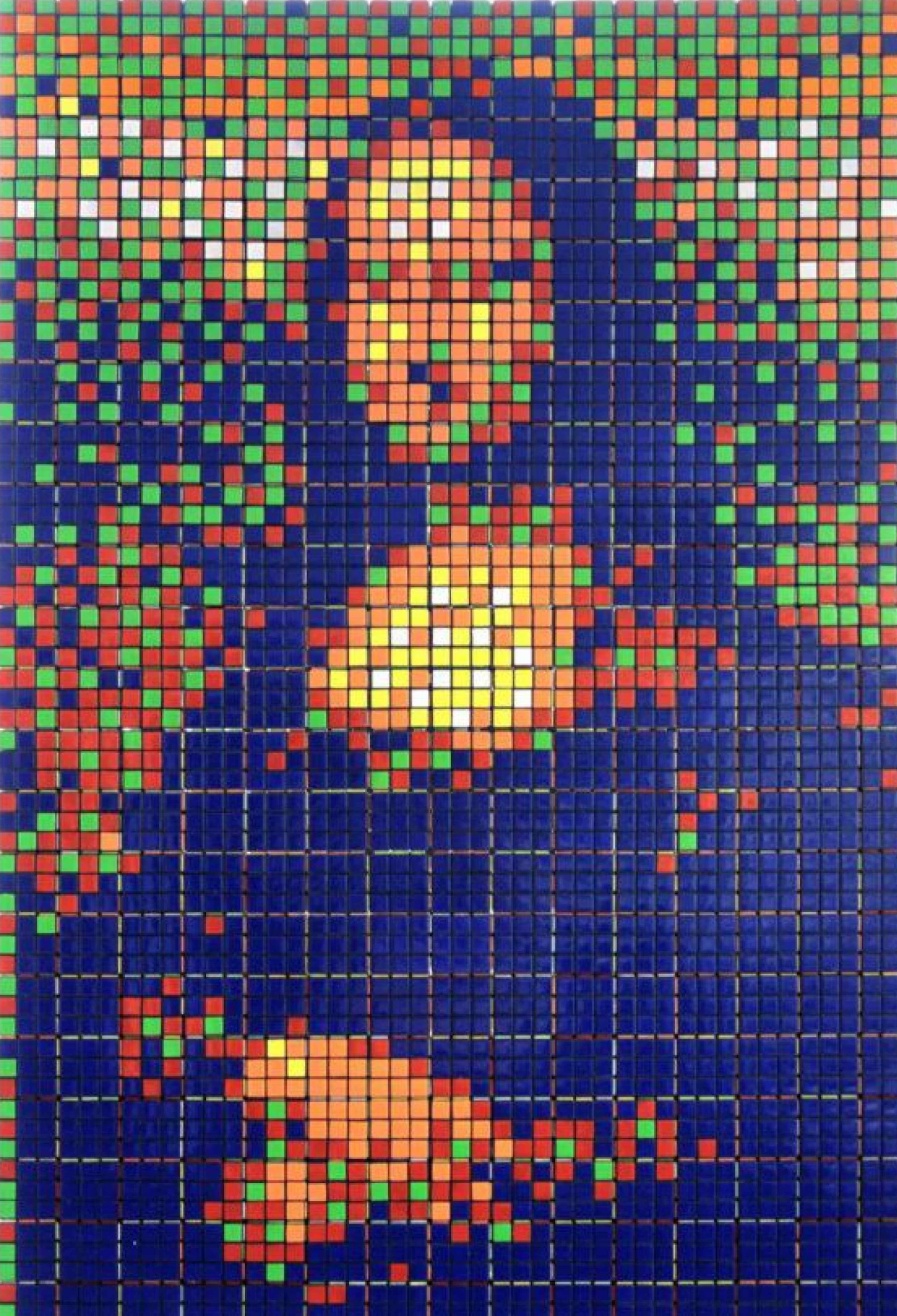
J'ai vu passer ici et là la news que la « Rubik Mona Lisa » de l'artiste Invader sera mise en enchère le 23 février à Paris. J'adore l'idée du Rubikcubisme mais ce n'est pas dans mes moyens (prix estimé 120-150 K€). EDIT : vendu pour 48,2K€, c'est définitivement pas pour moi ! Je pourrais donc peut-être le copier ? Mais avant d'investir 4K€ en Rubik's cubes (ce qui n'est pas dans mes moyens non plus, mais plus facilement envisageable 😉), j'ai décidé de produire une image pour voir si ça rend bien.

Les nombreux articles que j'ai lus disent que l'œuvre est composée de (près de) 330 Rubik's cubes. La Joconde de Leonardo fait 53 x 77 cm. En supposant qu'Invader a essayé d'avoir un format proche de l'original, faisons quelques calculs :

$ calc

; r=53/77
; sqrt(330*r)
	15.07125930846049582551
; 330/15
	22

On aurait donc 15 x 22 cubes ou 45 x 66 « pixels ». Si ce sont des cubes standard, le tableau doit mesurer environ 85 x 125 cm avec une densité de 1.33 dpi. Cool !

Première tâche, trouver une image de la Joconde en bonne résolution. Rapide recherche sur Google images, je tombe ici. 1400 x 2052 pixels, magnifique ! Heureusement j'ai un écran 4K me permettant de voir l'image entier en 100%. Un petit passage par Gimp pour couper un peu les bords afin de passer à 1350 x 1980, soit (30 * 45) x (30 * 66) et c'est parti !

Première tentative

Tout d'abord je dois réduire la taille de mon image à 45 x 66 pixels. Euh, pourquoi j'ai cherché une image de bonne résolution ? 😕 Au début je pensais séparer l'image en carrés 30 x 30 et calculer la couleur moyenne de chaque carrée, mais j'ai décidé de faire confiance à Processing qui doit faire à peu près la même chose mais peut-être mieux :

final int LISA_W = 15 * 3;
final int LISA_H = 22 * 3;
final int LISA_PSIZE = 30;

PImage lisa = loadImage("joconde1350x1980.jpg");
lisa.resize(LISA_W, LISA_H);
lisa.loadPixels();

Maintenant il ne reste qu'à agrandir les pixels et les dessiner en carrés :

stroke(0);
int i = 0;
for (int y = 0; y < LISA_H; y++) {
  for (int x = 0; x < LISA_W; x++) {
    fill(lisa.pixels[i++]);
    rect(x * LISA_PSIZE, y * LISA_PSIZE, LISA_PSIZE, LISA_PSIZE, LISA_PSIZE / 6);
  }
}

Et voici le résultat (click droit sur l'image pour la voir en taille réelle):

Pas mal !

Maintenant les choses semblent simples : remplacer la couleur de chaque pixel par la couleur du Rubik's cube la plus proche et le tour est joue !

Mais quelles sont les couleurs du Rubik's cube ? En googlant, je tombe sur cette palette qui me plaît bien :

final color[] RUBIK_COLORS = {
  #009B48, // green
  #B90000, // red
  #0045AD, // blue
  #FF5900, //orange
  #FFFFFF, // white
  #FFD500, // yellow
};

Pour mesurer la « proximité » entre deux couleurs, je les considère comme des points dans un espace 3D (RGB) et j'utilise la distance Euclidienne :

float distColor(color c1, color c2) {
  return dist(red(c1), green(c1), blue(c1), red(c2), green(c2), blue(c2));
}

Et pour trouver la couleur la plus proche dans une palette :

color closestColor(color c, color[] palette) {
  int closest = 0;
  float dMin = distColor(c, palette[0]);

  for (int i = 1; i < palette.length; i++) {
    float d = distColor(c, palette[i]);
    if (d < dMin) {
      closest = i;
      dMin = d;
    }
  }

  return palette[closest];
}

Maintenant, pour dessiner l'image en couleurs Rubik's cube, il faut juste légèrement modifier le corps de la boucle qui parcourt les pixels ;

for (int y = 0; y < LISA_H; y++) {
  for (int x = 0; x < LISA_W; x++) {
    fill(closestColor(lisa.pixels[i++], RUBIK_COLORS));
    rect(x * LISA_PSIZE, y * LISA_PSIZE, LISA_PSIZE, LISA_PSIZE, LISA_PSIZE / 6);
  }
}

Bah quoi ? C'est mon interprétation de la Joconde et je l'assume !

Ok, les couleurs, ce n'est pas si simple. J'ai un plan qui va peut-être marcher mieux :

• Réduire le nombre des couleurs de l'image originale à 6
• Faire un mapping entre les 6 couleurs ainsi obtenues et les 6 couleurs du Rubik's cube

Quantification

La quantification des couleurs est une technique qui consiste à réduire le nombre des couleurs d'une image en la gardant visuellement proche de l'original. Le principe est de regrouper les couleurs proches en clusters et de prendre le « centre » de chaque cluster comme couleur représentatif. On considère toujours les couleurs comme des points dans un espace euclidien et on applique des techniques de clustering standard. C'est parti donc pour implanter la méthode des k-means. Et puisque on y est, faisons les choses proprement pour que la méthode puisse s'appliquer non seulement aux couleurs mais à n'importe quelles données.

Le fonctionnement des k-means est très simple :

while(assignClusters()) updateCentroids();

assignClusters() attribue à chaque point le cluster dont le barycentre est le plus proche. updateCentroids() recalcule les barycentres selon la dernière attribution des clusters. On s'arrête quand aucun point ne change de cluster. On initialise en attribuant à chaque point un cluster au hasard.

J'ai fait une petite classe et avant de l'utiliser pour les couleurs, un test rapide ici afin de m'assurer qu'elle fonctionne bien.

Bon, passons maintenant à l'application des k-means sur notre image. Tout d'abord deux fonctions de conversion entre tableau et couleur :

// converts Processing's color to array of [r, g, b]
void colorToRgb(color c, float[] rgb) {
  rgb[0] = red(c);
  rgb[1] = green(c);
  rgb[2] = blue(c);
}

// converts array of [r, g, b] to Processing's color
color rgbToColor(float[] rgb) {
  return color(rgb[0], rgb[1], rgb[2]);
}

Et ensuite :

lisa.loadPixels();

// Prepare data for k-means
float[][] arrPixels = new float[lisa.pixels.length][3];
for (int i = 0; i < lisa.pixels.length; i++) {
  colorToRgb(lisa.pixels[i], arrPixels[i]);
}

// Run k-means
KMeans km = new KMeans(arrPixels, RUBIK_COLORS.length);
km.compute();

// use the palette found by k-means
for (int i = 0; i < lisa.pixels.length; i++) {
  lisa.pixels[i] = rgbToColor(km.getCentroid(km.getCluster(i)));
}

lisa.updatePixels();

Tadaaam ! En haut à gauche la palette calculée par k-means, à droite l'image original pour comparaison.

À noter que les résultats son légèrement différents à chaque exécution car k-means trouve un optimum local et l'attribution initiale de clusters se fait aléatoirement.

Bon, je sais, je peux faire ça avec Gimp en 10 secondes, mais on apprend beaucoup en faisant les choses tout seul comme un grand. En plus, c'est facile d'observer le fonctionnement de k-means itération par itération :

Jouons encore un peu avec les couleurs. Un passage ici a attiré mon attention.

The three color channels are usually red, green, and blue, but another popular choice is the Lab color space, in which Euclidean distance is more consistent with perceptual difference.

Mais c'est quoi cet espace Lab ? Bon, j'avoue que je n'ai pas tout compris, mais pour ma défense, c'est une invention d'illuminés 😃.

En revanche, j'ai choppé des formules de conversion ici. L'implantation de ces formules fut longue et pénible et le code résultant très, très moche. Mais j'ai tenté une conversion RGB -> Lab -> RGB sur l'image original et surprise, ça a marché du premier coup !

Juste pour le fun, un dégradé allant de pur vert à pur bleu avec une interpolation linéaire dans RGB, Lab et HSB :

Pour plus d'information sur les couleurs, je recommande ce livre.

Voici une comparaison entre les quantifications dans les deux espaces. À gauche RGB, à droite Lab.

J'ai du mal à décider laquelle je préfère. À gauche on a beaucoup plus de détails, mais à droite on a moins de bleu sur la peau et les couleurs sont peut-être plus naturelles.

Bon, maintenant je dois transformer mon image initiale de 1350 x 1980 pixels à 31744 couleurs en image de 45 x 66 pixels à 6 couleurs. En gros, cela correspond à une perte d'information de 17K fois ! J'ai plusieurs possibilités.

Image à quantifier :

1. Quantifier l'image original. Partager-la en carrés de 30 x 30, trouver la couleur la plus fréquente pour chaque carré qui sera la couleur du pixel correspondant de l'image rétrécie.
2. Rétrécir l'image original en utilisant PImage.resize(). Quantifier l'image rétrécie.

Espace colorimétrique :

1. RGB
2. Lab

Le produit cartésien (image à quantifier x espace) donne cela :

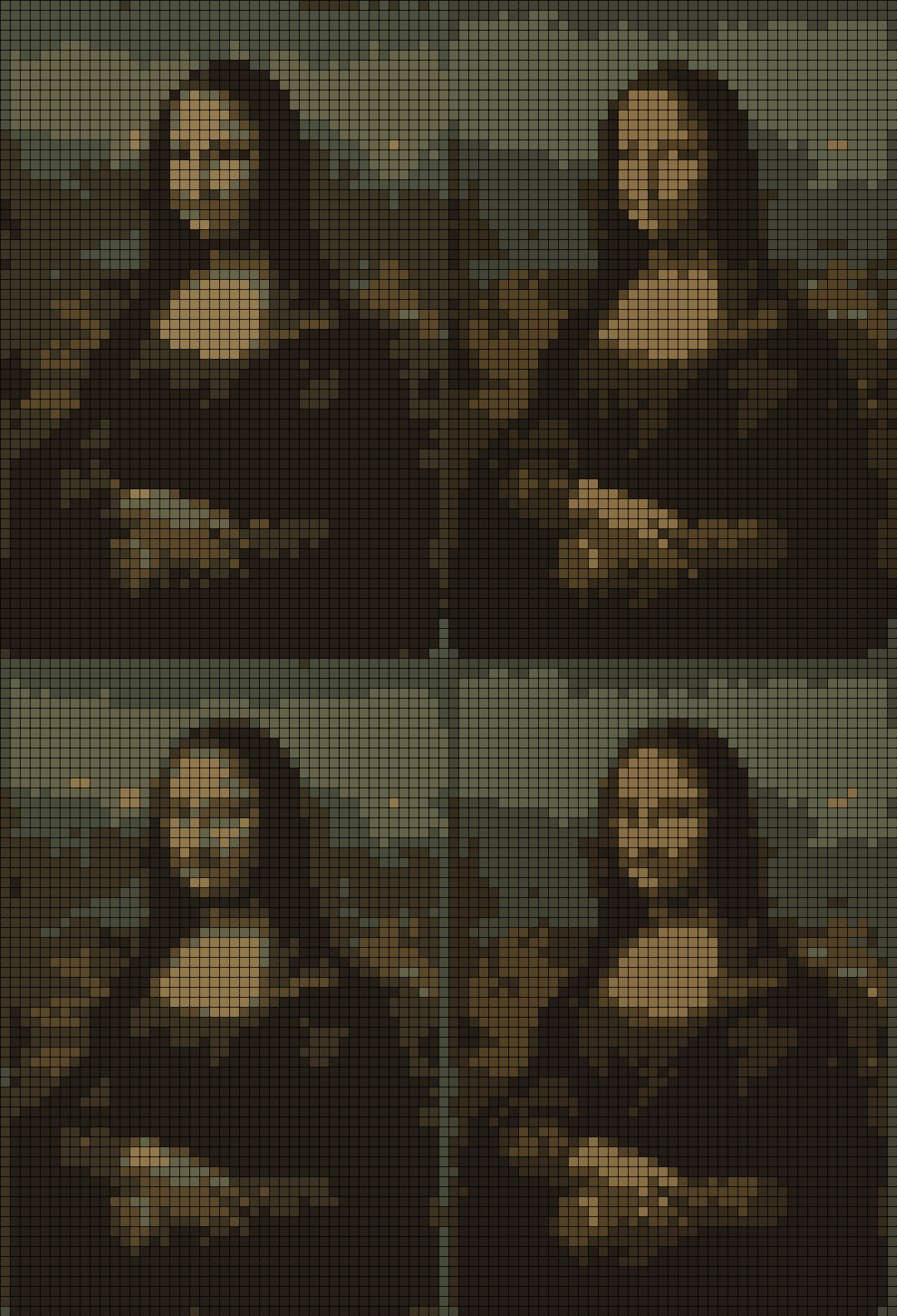
Les lignes sont l'image de départ et les colonnes l'espace couleur. Encore une fois, les résultats varient d'une exécution à l'autre, mais étonnement, la plupart du temps je préfère 21 (image rétrécie / RGB). Intuitivement, j'ai misé tout le contraire, 12 (image original, Lab). Comme quoi, il ne faut pas se fier à son intuition !

Le code qui fait cette comparaison est ici. Le nom de la classe QImage est un clin d'œil à PImage et ses pixels sont des indices dans sa palette.

Problème d'affectation

Maintenant il ne nous reste qu'à passer de la palette douce et pastelle de notre Joconde quantifiée à la palette vive et joyeuse du Rubik's cube. Juste pour rigoler, commençons par un remplacement aléatoire:

Bon, ce n'est pas terrible. Une approche plus intelligente serait de résoudre un problème d'affectation. Ce problème peut être formulé ainsi :

Nous avons n agents (couleurs de la palette quantifiée) et n tâches (couleurs de la palette Rubik). Chaque agent doit réaliser exactement une tâche et chaque tâche doit être réalisée (chaque couleur de la première palette doit être remplacée par une couleur de la deuxième et chaque couleur de la deuxième doit être présent). Affecter la tâche j à l'agent i nous coûte c[i][j] (la distance entre la couleur i de la première palette et la couleur j de la deuxième est c[i][j]). Le but est de minimiser le coût total (la somme des distances entre des paires de couleurs remplacées).

J'ai une certaine culture RO et j'ai honte de ce que je vais faire, mais j'ai trop la flemme d'implanter l'algorithme hongrois qui s'exécute en O(n³). À la place, je vais brute-forcer en générant toutes les n! affectations possibles et en calculant le coût de chacune. Pour ma défense, pour n = 6 on ne remarquera pas vraiment la différence du temps d'exécution.

Il y a beaucoup de méthodes pour générer toutes les permutations de n éléments. J'ai choisi de les générer en ordre lexicographique. Étant donné une permutation a, voici comment on trouve la suivante dans l'ordre lexicographique :

1. Trouver le plus grand j tel que a[j] < a[j + 1]. S'il y en a pas, stop, c'est la dernière permutation.
2. Trouver le plus grand l tel que a[j] < a[l]. Permuter a[j] et a[l].
3. Renverser a[j + 1] ... a[n - 1]

En code, cela se traduit en :

boolean nextPerm(int[] a) {
  int j, l, t;

  // Find the biggest j such that a[j] < a[j + 1]
  for (j = a.length - 2; j>= 0 && a[j] >= a[j + 1]; j--);
  // If not such j, stop, this is the last permutation
  if (j == -1) return false;
  // Find the biggest l such that a[j] < a[l]
  for (l = a.length - 1; a[j] >= a[l]; l--);
  // Swap a[j] and a[l]
  t = a[j]; a[j] = a[l]; a[l] = t;
  // Reverse a[j + 1] ... a[n - 1]
  for (j++, l = a.length - 1; j < l; j++, l--) {
    t = a[j]; a[j] = a[l]; a[l] = t;
  }
  return true;
}

Si par exemple on veut afficher toutes les permutations, on peut utiliser quelque chose comme :

int[] a = new int[4];

void setup() {
  for (int i = 0; i < a.length; i++) a[i] = i;
}

void draw() {
  println(java.util.Arrays.toString(a));
  if (!nextPerm(a)) noLoop();
}

Quand on sait générer toutes les permutations, calculer l'affectation optimale devient un jeu d'enfant. Et quand on sait calculer l'affectation optimale, il est facile d'affecter les couleurs Rubik à la palette de Lisa. Il suffit de préparer la matrice des coûts :

PImage lisa = loadImage("joconde1350x1980.jpg");
lisa.resize(LISA_W, LISA_H);

int k = RUBIK_COLORS.length;
QImage lisaQ = new QImage(lisa, k, RGB);

// compute cost matrix
float[][] costs = new float[k][k];
float[][] lisaRgb = new float[k][3];
float[][] rubikRgb = new float[k][3];

for (int c = 0; c < k; c++) {
  colorToRgb(lisaQ.palette[c], lisaRgb[c]);
  colorToRgb(RUBIK_COLORS[c], rubikRgb[c]);
}

for (int i = 0; i < k; i++) {
  for (int j = 0; j < k; j++) {
    costs[i][j] = sqrt(sqDist(lisaRgb[i], rubikRgb[j]));
  }
}

// assign Rubik colors to Lisa's palette
Assignment ass = new Assignment(costs);
ass.compute();

// display the assignment
for (int c = 0; c < k; c++) {
  fill(lisaQ.palette[c]);
  rect(100 * c, 0, 100, 100);
  fill(RUBIK_COLORS[ass.getPair(c)]);
  rect(100 * c, 100, 100, 100);
}

Cela me semble pertinent, j'aurais fait pareil à la main. D'ailleurs en utilisant colorToLab() à la place de colorToRgb() j'obtiens la même affectation. Et j'ass-ume les noms de mes variables !

On est pas loin du but ! Il ne reste qu'à mettre ce code dans une méthode changePalette() de la classe QImage et de l'appeler avant de dessiner Lisa. Et voilà !

Bon, ma Lisa est beaucoup moins belle que celle d'Invader mais je l'aime bien quand-même.

Ce sketch génère une nouvelle Lisa à chaque click de la souris. En jouant avec, je constate que je tombe toujours sur quelques images typiques qui doivent correspondre aux minima locaux trouvés par k-means.

Ce sketch génère 12 Lisas suffisamment distinctes (pixels en commun < 95%) :

Pour y arriver, j'ai dû faire 255 343 tentatives et faire tourner le ventilo. Les touches brûlent encore mes doigts pendant que j'écris ceci 😃. On remarque que dans certaines images il manque une ou plusieurs couleurs, il y en a une carrément monochrome. Ceci signifie que k-means a produit des clusters vides.

Bonus

Ce qui est bien avec le code est que quand on sait Rubik-cubiser la Joconde, on sait transformer n'importe quelle image sans tout recommencer from scratch. Je vais compléter cette section avec quelques tableaux célèbres.

---

Hexaèdre bleu, 18 x 18 cubes, RGB quantization, 19 février 2020 (tableau original)

Proposé par @RecRuinLandscp

---

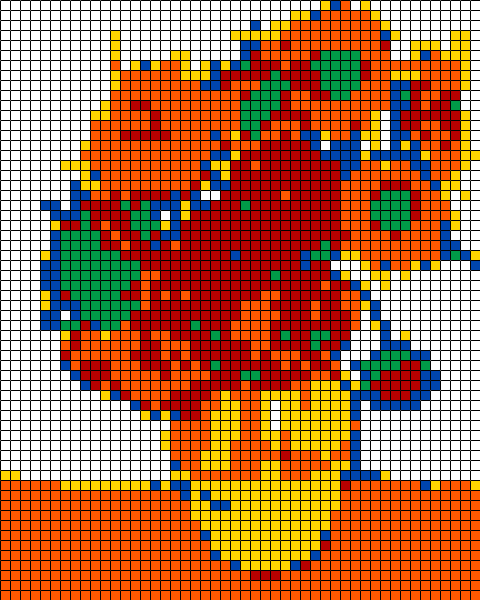
Vase avec douze tournecubes, 16 x 20 cubes, RGB quantization, 20 février 2020 (tableau original)

---

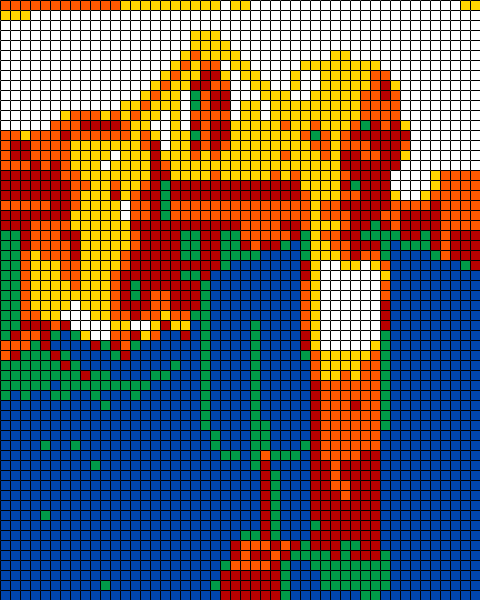
American Rubik, 16 x 20 cubes, RGB quantization, 21 février 2020 (tableau original)

---

Can't solve this cube!, 16 x 20 cubes, Lab quantization, 22 février 2020 (tableau original)

---

Impression, carré levant, 20 x 16 cubes, RGB quantization, seed 19865, 23 février 2020, (tableau original)

---

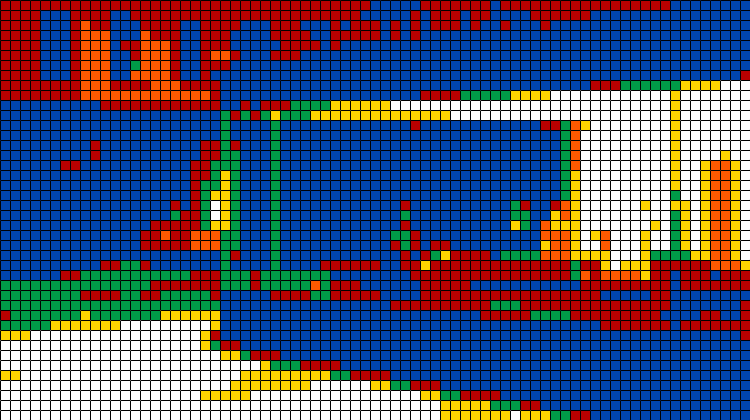
Nightcubers, 25 x 14 cubes, RGB quantization, seed 2321, 24 février 2020. (tableau original)

---

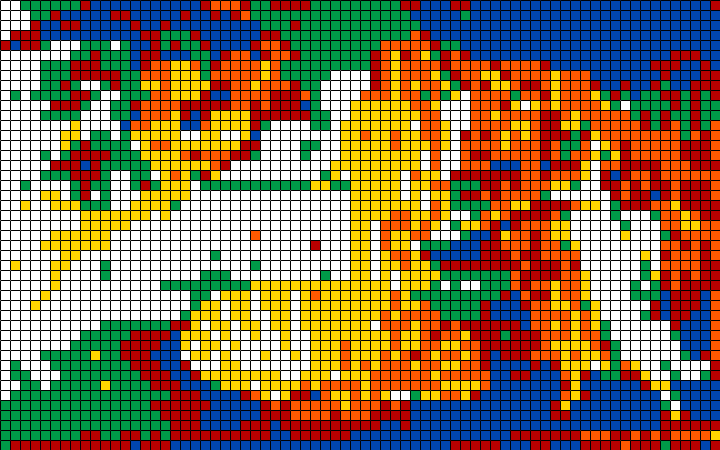
The birth of Cubus (Cubotticelli), 24 x 15 cubes, Lab quantization, seed 3000, 25 février 2020. (tableau original)

---

Cheval de cubes, 22 x 15 cubes, Lab quantization, seed 150592, 26 février 2020. (tableau original)

---

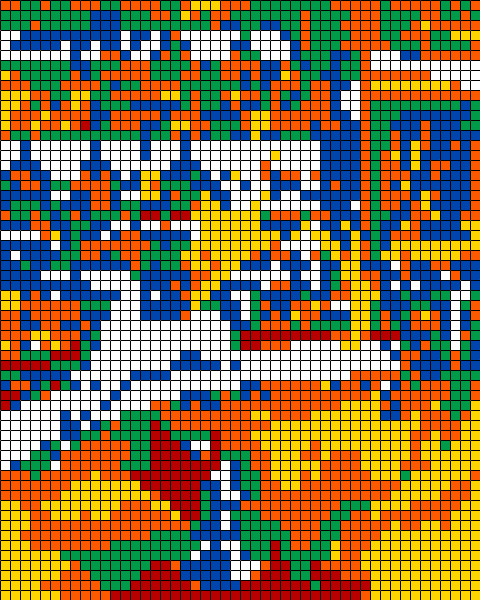
The Rubik's Circus, 16 x 20 cubes, Lab quantization, seed 81191, 26 février 2020. (tableau original)

---

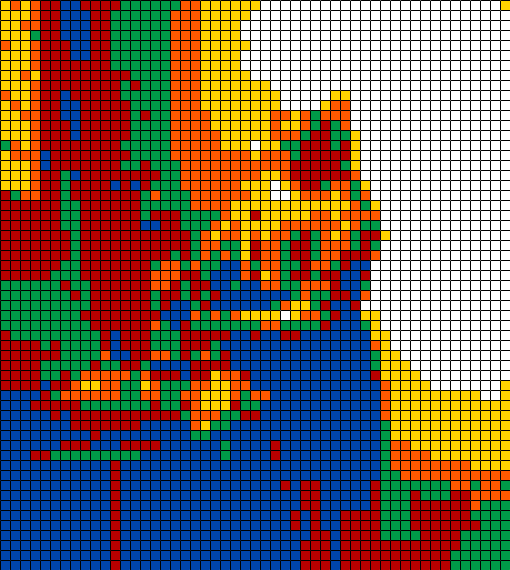
The Rubikmaid, 17 x 19 cubes, RGB quantization, seed 90263, 27 février 2020. (tableau original)

---

Le fils du cube, 15 x 22 cubes, Lab quantization, seed 6569, 28 février 2020. (tableau original)

---

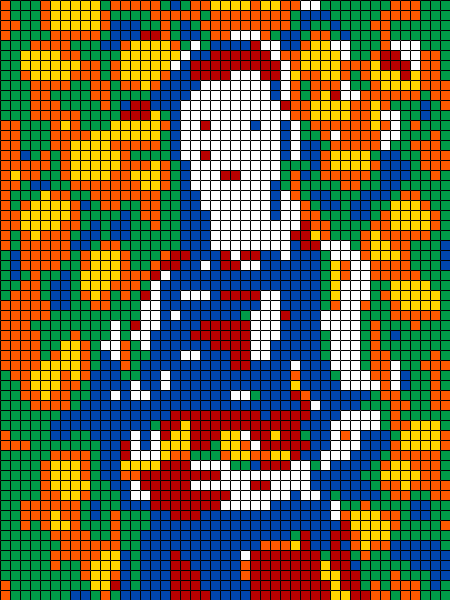
Момиче с кубове (A girl with cubes), 15 x 22 cubes, Lab quantization, seed 152552, 29 février 2020. (tableau original)

---

Frida con collar de cubos, 16 x 20 cubes, RGB quantization, seed 28926, 1er mars 2020. (tableau original)

---

Élisabeth au chapeau de cubes, 15 x 22 cubes, RGB quantization, seed 80992, 2 mars 2020. (tableau original)

---

La grande vague de Cubewaga, 22 x 15 cubes, RGB quantization, seed 60190, 2 mars 2020. (tableau original)

---

La persistance du cube, 21 x 16 cubes, RGB quantization, seed 24521, 3 mars 2020. (tableau original)

---

La danse des cubes, 22 x 15 cubes, Lab quantization, seed 1497, 4 mars 2020. (tableau original)

---

The Rubikiss, 18 x 18 cubes, RGB quantization, seed 8316, 5 mars 2020. (tableau original)

---

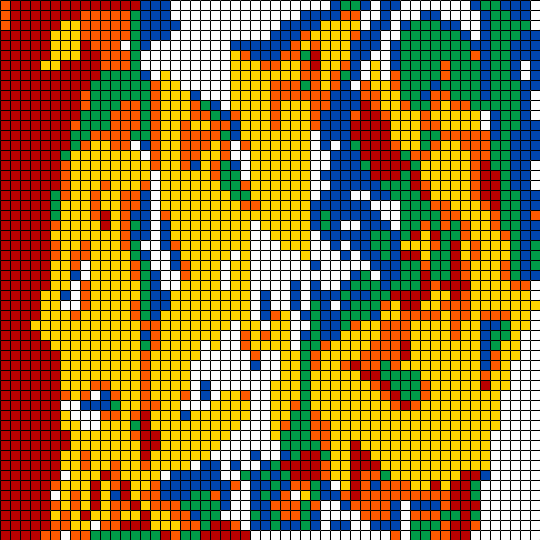
Les cubes d'Avignon, 18 x 18 cubes, Lab quantization, seed 2565, 6 mars 2020. (tableau original)

---