-
-
Notifications
You must be signed in to change notification settings - Fork 60
Python Geometry
The Geometry object is a class containing coordinates
of atomic elements. For each atom attached to the geometry
an Atom object is attached.
Also the Geometry class enherits a multitude of the
SuperCell class which enables a unified
class to contain information about a full simulation cell.
The simplest way to create a Geometry is
geom = sisl.Geometry([[0,0,0],[1,1,1]])
which is a 2-atom Geometry with atoms located at origo
and another shifted by 1 Å along each Cartesian coordinate.
sisl will automatically guess the SuperCell to be
[2,2,2]. This is done per the Cartesian bond-lengths along each direction.
Any Geometry can have arbitrarily many atoms and any combination of
atomic species.
For creating the graphene honeycomb unit cell you can do this
sc = sisl.SuperCell([[1.5, 3.**.5 * 0.5, 0.],
[1.5,-3.**.5 * 0.5, 0.],
[0. , 0. ,10.]], nsc=[3,3,1])
g = sisl.Geometry([[0.,0.,0.],[1.,0.,0.]], atom=sisl.Atom[6], sc=sc)
where the bond-length is 1 Å.
Similarly to generate hexagonal boron nitride the following change suffices
g = sisl.Geometry([[0.,0.,0.],[1.,0.,0.]],
atom=[sisl.Atom[5],sisl.Atom[7]], sc=sc)
sisl implement several standard lattice structures defined in sisl.geom.
The following geometries are present
from sisl import Atom
from sisl.geom import *
honeycomb(1.42,Atom(6)) # graphene
honeycomb(1.42,Atom(6), orthogonal=True) # graphene in an orthogonal unit-cell
honeycomb(1.42,[Atom(5),Atom(7)]) # Hexagonal boron-nitride
honeycomb(1.42,[Atom(5),Atom(7)], orthogonal=True) # Orthogonal hexagonal boron-nitride
graphene() # shorthand for `honeycomb(1.42,Atom(6))`
graphene(orthogonal=True) # shorthand for `honeycomb(1.42,Atom(6),orthogonal=True)`
sc(alat,Atom) # Simple Cubic lattice
bcc(alat,Atom) # BCC lattice
fcc(alat,Atom) # FCC lattice
hcp(alat,Atom) # HCP lattice
diamond(alat,Atom) # diamond lattice
The Geometry class implements several routines to retrieve information about neighbours
and manipulations.
Note that sgeom is a utility for
using several of the methods inherent to the Geometry class.
Creating a graphene flake of 40.000 atoms
from sisl.geom import graphene
g = graphene().tile(200, 0).tile(100, 1)
g = graphene(orthogonal=True).tile(100, 0).tile(100, 1)
which creates a skewed unit cell axis or an orthogonal cell, respectively.
We will here highlight a few methods inherent to the class
-
tile/repeat(int, axis)Expanding the geometry by adding more unit cells in the given lattice directions. Each routine takes an integer to denote number of times it is repeated, and the axis decides which lattice vectors will be expanded. The underlying SuperCell object also gets expanded.
-
close(int|xyz,...)Returns an array of indices with elements within a certain radius of the, 1) atom corresponding to the integer index, or 2) coordinate given by the vector
xyz.This is handy for geometry creation as well as finding atoms close to other atoms.
-
sub(list)Returns a new geometry only with the requested atoms.
-
remove(list)Returns a new geometry with all other than the removed atoms.
-
append(other, axis)Extends another geometry on top of the current one in the direction of the axis lattice vector.
-
prepend(other, axis)Extends another geometry below of the current one in the direction of the axis lattice vector. This is equivalent to
appendbut with the order of the atoms being theother, then the current atoms.
The geometry is attached a SuperCell object which holds information about the geometry periodicity.
As an example we will create a geometry as
import sisl
sc = sisl.SuperCell([0.5,1,20]) # nsc = [1,1,1] default
A = sisl.Atom(1,R=0.36) # Nearest neighbour interaction
g = sisl.Geometry([[0.15,0.1,0],[0.4,0.35,0],
[0.15,0.6,0],[0.4,0.85,0]], atom=A, sc=sc)
which results in this geometry
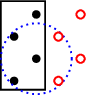
where all the black dots are the atoms, and the circle is the interaction range,
(orbital range).
However, the auxiliary cell is not big enough to encompass all connections.
So if one uses the close method to retrieve all neighbours of any of the atoms
the connection scheme will be erroneous. Two of the atoms will connect to 1 other atom
and the other two atoms will connect to 2 other atoms.
To correct the super cell we update the number of auxiliary cells by
g.set_nsc([3,3,1])
which results in the following structure
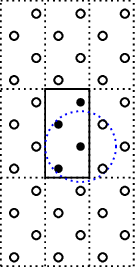
where all connections are correctly found, any atom will connect to 4 atoms.
If the orbitals in the system have a much larger interaction range we will again
find an inconsistency in the number of atoms that is connected. For instance
by making the interaction range Atom(1,R=1.1), but only nsc=[3,3,1] will
result in
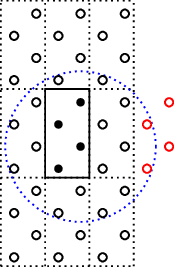
which again becomes too small.
The auxiliary cell is extremely important in defining Hamiltonian models where the interaction range and found neighbours are very important.