-
-
Notifications
You must be signed in to change notification settings - Fork 208
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
1 parent
3d11a70
commit 5864e65
Showing
7 changed files
with
206 additions
and
79 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -1,75 +1,136 @@ | ||
| # Using `ahmc_bayesian_pinn_pde` with the `BayesianPINN` Discretizer for the 1-D Burgers' Equation | ||
| # Using `ahmc_bayesian_pinn_pde` with the `BayesianPINN` Discretizer for the Kuramoto–Sivashinsky equation | ||
|
|
||
| Let's consider the Burgers' equation: | ||
| Consider the Kuramoto–Sivashinsky equation: | ||
|
|
||
| ```math | ||
| \begin{gather*} | ||
| ∂_t u + u ∂_x u - (0.01 / \pi) ∂_x^2 u = 0 \, , \quad x \in [-1, 1], t \in [0, 1] \, , \\ | ||
| u(0, x) = - \sin(\pi x) \, , \\ | ||
| u(t, -1) = u(t, 1) = 0 \, , | ||
| \end{gather*} | ||
| ∂_t u(x, t) + u(x, t) ∂_x u(x, t) + \alpha ∂^2_x u(x, t) + \beta ∂^3_x u(x, t) + \gamma ∂^4_x u(x, t) = 0 \, , | ||
| ``` | ||
|
|
||
| with Bayesian Physics-Informed Neural Networks. Here is an example of using `BayesianPINN` discretization with `ahmc_bayesian_pinn_pde` : | ||
| where $\alpha = \gamma = 1$ and $\beta = 4$. The exact solution is: | ||
|
|
||
| ```math | ||
| u_e(x, t) = 11 + 15 \tanh \theta - 15 \tanh^2 \theta - 15 \tanh^3 \theta \, , | ||
| ``` | ||
|
|
||
| where $\theta = t - x/2$ and with initial and boundary conditions: | ||
|
|
||
| ```math | ||
| \begin{align*} | ||
| u( x, 0) &= u_e( x, 0) \, ,\\ | ||
| u( 10, t) &= u_e( 10, t) \, ,\\ | ||
| u(-10, t) &= u_e(-10, t) \, ,\\ | ||
| ∂_x u( 10, t) &= ∂_x u_e( 10, t) \, ,\\ | ||
| ∂_x u(-10, t) &= ∂_x u_e(-10, t) \, . | ||
| \end{align*} | ||
| ``` | ||
|
|
||
| With Bayesian Physics-Informed Neural Networks, here is an example of using `BayesianPINN` discretization with `ahmc_bayesian_pinn_pde` : | ||
|
|
||
| ```@example low_level_2 | ||
| using NeuralPDE, Lux, ModelingToolkit | ||
| import ModelingToolkit: Interval, infimum, supremum | ||
| using NeuralPDE, Flux, Lux, ModelingToolkit, LinearAlgebra, AdvancedHMC | ||
| import ModelingToolkit: Interval, infimum, supremum, Distributions | ||
| using Plots, MonteCarloMeasurements | ||
| @parameters t, x | ||
| @parameters x, t, α | ||
| @variables u(..) | ||
| Dt = Differential(t) | ||
| Dx = Differential(x) | ||
| Dxx = Differential(x)^2 | ||
| Dx2 = Differential(x)^2 | ||
| Dx3 = Differential(x)^3 | ||
| Dx4 = Differential(x)^4 | ||
| # α = 1 | ||
| β = 4 | ||
| γ = 1 | ||
| eq = Dt(u(x, t)) + u(x, t) * Dx(u(x, t)) + α * Dx2(u(x, t)) + β * Dx3(u(x, t)) + γ * Dx4(u(x, t)) ~ 0 | ||
| #2D PDE | ||
| eq = Dt(u(t, x)) + u(t, x) * Dx(u(t, x)) - (0.01 / pi) * Dxx(u(t, x)) ~ 0 | ||
| u_analytic(x, t; z = -x / 2 + t) = 11 + 15 * tanh(z) - 15 * tanh(z)^2 - 15 * tanh(z)^3 | ||
| du(x, t; z = -x / 2 + t) = 15 / 2 * (tanh(z) + 1) * (3 * tanh(z) - 1) * sech(z)^2 | ||
| # Initial and boundary conditions | ||
| bcs = [u(0, x) ~ -sin(pi * x), | ||
| u(t, -1) ~ 0.0, | ||
| u(t, 1) ~ 0.0, | ||
| u(t, -1) ~ u(t, 1)] | ||
| bcs = [u(x, 0) ~ u_analytic(x, 0), | ||
| u(-10, t) ~ u_analytic(-10, t), | ||
| u(10, t) ~ u_analytic(10, t), | ||
| Dx(u(-10, t)) ~ du(-10, t), | ||
| Dx(u(10, t)) ~ du(10, t)] | ||
| # Space and time domains | ||
| domains = [t ∈ Interval(0.0, 1.0), | ||
| x ∈ Interval(-1.0, 1.0)] | ||
| domains = [x ∈ Interval(-10.0, 10.0), | ||
| t ∈ Interval(0.0, 1.0)] | ||
| # Discretization | ||
| dx = 0.05 | ||
| dx = 0.4; | ||
| dt = 0.2; | ||
| # Function to compute analytical solution at a specific point (x, t) | ||
| function u_analytic_point(x, t) | ||
| z = -x / 2 + t | ||
| return 11 + 15 * tanh(z) - 15 * tanh(z)^2 - 15 * tanh(z)^3 | ||
| end | ||
| # Function to generate the dataset matrix | ||
| function generate_dataset_matrix(domains, dx, dt) | ||
| x_values = -10:dx:10 | ||
| t_values = 0.0:dt:1.0 | ||
| dataset = [] | ||
| for t in t_values | ||
| for x in x_values | ||
| u_value = u_analytic_point(x, t) | ||
| push!(dataset, [u_value, x, t]) | ||
| end | ||
| end | ||
| return vcat([data' for data in dataset]...) | ||
| end | ||
| datasetpde = [generate_dataset_matrix(domains, dx, dt)] | ||
| plot(datasetpde[1][:, 2], datasetpde[1][:, 1], title="Dataset from Analytical Solution") | ||
| # Add noise to dataset | ||
| datasetpde[1][:, 1] = datasetpde[1][:, 1] .+ randn(size(datasetpde[1][:, 1])) .* 5 / 100 .* | ||
| datasetpde[1][:, 1] | ||
| plot!(datasetpde[1][:, 2], datasetpde[1][:, 1]) | ||
| # Neural network | ||
| chain = Lux.Chain(Lux.Dense(2, 10, Lux.σ), Lux.Dense(10, 10, Lux.σ), Lux.Dense(10, 1)) | ||
| strategy = NeuralPDE.GridTraining([dx,dx]) | ||
| chain = Lux.Chain(Lux.Dense(2, 8, Lux.tanh), | ||
| Lux.Dense(8, 8, Lux.tanh), | ||
| Lux.Dense(8, 1)) | ||
| discretization = NeuralPDE.BayesianPINN([chain], strategy) | ||
| discretization = NeuralPDE.BayesianPINN([chain], | ||
| GridTraining([dx, dt]), param_estim = true, dataset = [datasetpde, nothing]) | ||
| @named pde_system = PDESystem(eq, bcs, domains, [x, t], [u(x, t)]) | ||
| @named pde_system = PDESystem(eq, | ||
| bcs, | ||
| domains, | ||
| [x, t], | ||
| [u(x, t)], | ||
| [α], | ||
| defaults = Dict([α => 0.5])) | ||
| sol1 = ahmc_bayesian_pinn_pde(pde_system, | ||
| discretization; | ||
| draw_samples = 100, | ||
| bcstd = [0.01, 0.03, 0.03, 0.01], | ||
| phystd = [0.01], | ||
| draw_samples = 100, Kernel = AdvancedHMC.NUTS(0.8), | ||
| bcstd = [0.2, 0.2, 0.2, 0.2, 0.2], | ||
| phystd = [1.0], l2std = [0.05], param = [Distributions.LogNormal(0.5, 2)], | ||
| priorsNNw = (0.0, 10.0), | ||
| saveats = [1 / 100.0, 1 / 100.0],progress=true) | ||
| saveats = [1 / 100.0, 1 / 100.0], progress = true) | ||
| ``` | ||
|
|
||
| And some analysis: | ||
|
|
||
| ```@example low_level | ||
| using Plots | ||
| ts, xs = [infimum(d.domain):0.01:supremum(d.domain) for d in domains] | ||
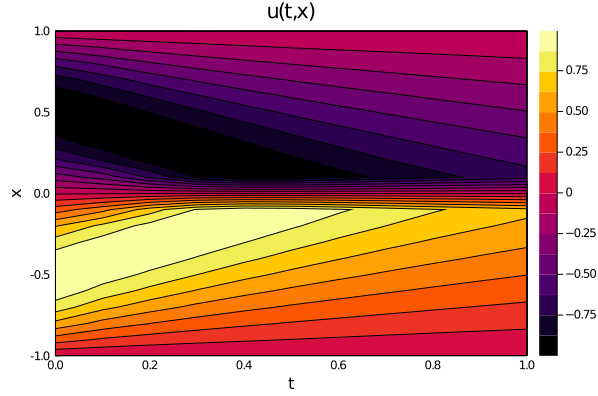
| u_predict_contourf = reshape([first(phi([t, x], res.u)) for t in ts for x in xs], | ||
| length(xs), length(ts)) | ||
| plot(ts, xs, u_predict_contourf, linetype = :contourf, title = "predict") | ||
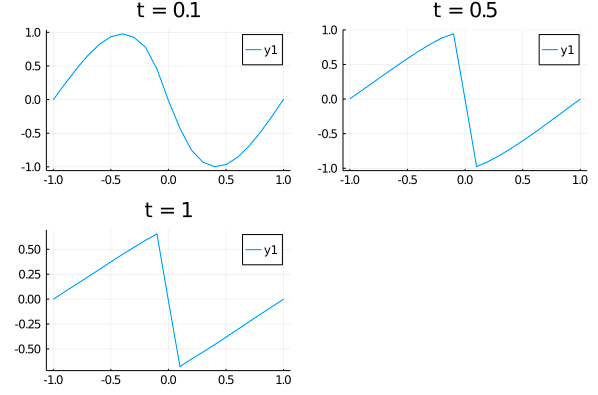
| u_predict = [[first(phi([t, x], res.u)) for x in xs] for t in ts] | ||
| p1 = plot(xs, u_predict[3], title = "t = 0.1"); | ||
| p2 = plot(xs, u_predict[11], title = "t = 0.5"); | ||
| p3 = plot(xs, u_predict[end], title = "t = 1"); | ||
| ```@example low_level_2 | ||
| phi = discretization.phi[1] | ||
| xs, ts = [infimum(d.domain):dx:supremum(d.domain) for (d, dx) in zip(domains, [dx / 10, dt])] | ||
| u_predict = [[first(pmean(phi([x, t], sol1.estimated_nn_params[1]))) for x in xs] | ||
| for t in ts] | ||
| u_real = [[u_analytic(x, t) for x in xs] for t in ts] | ||
| diff_u = [[abs(u_analytic(x, t) - first(pmean(phi([x, t], sol1.estimated_nn_params[1])))) | ||
| for x in xs] | ||
| for t in ts] | ||
| p1 = plot(xs, u_predict, title = "predict") | ||
| p2 = plot(xs, u_real, title = "analytic") | ||
| p3 = plot(xs, diff_u, title = "error") | ||
| plot(p1, p2, p3) | ||
| ``` | ||
|
|
||
|  | ||
|
|
||
|  |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
Oops, something went wrong.