Standard curves
Think of a standard curve as you think of a ruler, but it's a ruler that you have to create yourself, based on some known values. Standard curve is a concept/tool used to measure concentration or dilution. Unfortunately we can't measure it directly, so we measure the intensity of light, and using a standard curve, we translate the value we know to the value we want to know.
In many cases it's linear but not in our example. Curve we are trying to fit has logistic shape. Still the sample dilution is estimated the best (with the lowest variance) in a "liner" part of logistic curve.
You want to measure distance (easy to imagine) across values ranging from 0m to 1m. You have a rod of 1m in length and the ability to split it in half. While measuring distances close to 0, you want to split the rod in order to be more accurate. A shorter rod has more in common with numbers in this range. That is why, in the process of building a standard curve, it's best to use samples of various dilutions; we want to cover the whole range of possible dilutions so that test samples have some point of reference that makes sense for comparison (You don't want to measure the size of building with a ruler.
This one is more technical, but it illustrates the need for standard curves. Imagine you have a Naive Bayes machine learning model and want to predict probabilities with it. You know the one outputted by the model aren't quite right. Somehow, a miracle happened, and you know the actual probabilities for 1000 observations. Using this phenomenon, you can compare the real probabilities to the one your model outputs. It turns out that Naive Bayes shifts probabilities either to 0 or 1.
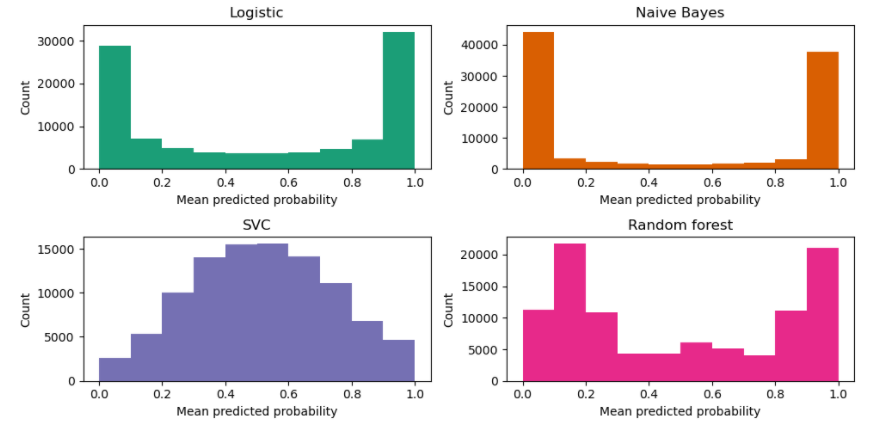
Equipped with this knowledge, we can "calibrate" our model outputs to better describe the reality of observed phenomena. Fun fact: curve similar to a sigmoid calibrates probabilities from the Naive Bayes model.
In this story, both values before and after calibration are in the realm of probabilities. That's not the case with the standard curves we are dealing with. Values before calibration are described using MFI, and after, we deal with dilutions or concentrations. But other than that, everything is analogous.