seqR is an R package for fast k-mer counting. It provides
- highly optimized (the core algorithm is written in C++)
- in-memory
- probabilistic (with configurable dimensionality of a hash value used for storing k-mers internally),
- multi-threaded (with a configurable size of the batch of
sequences (
batch_size) to process in a single step. Ifbatch_sizeequals 1, the multi-threaded mode is disabled, which potentially causes a longer computation time)
implementation that supports
- various variants of k-mers (contiguous, gapped, and positional counterparts)
- all biological sequences (e.g., nucleic acids and proteins)
Moreover, the result optimizes memory consumption by the application of sparse matrices (see package Matrix), compatible with machine learning packages such as ranger and xgboost.
To install seqR from CRAN:
install.packages("seqR")Alternatively, if you want to use the latest development version:
# install.packages("devtools")
devtools::install_github("slowikj/seqR")The package provides two functions that facilitate k-mer counting
count_kmers(used for counting k-mers of one type)count_multimers(a wrapper ofcount_kmers, used for counting k-mers of many types in a single invocation of the function)
and one function used for custom processing of k-mer matrices:
rbind_columnwise(a helper function used for merging several k-mer matrices that do not have same sets of columns)
To learn more, see features overview vignette and reference.
count_kmers(sequences=c("AAAAAVVAVFF", "DFGSADFGSA"),
k=5)
#> 2 x 12 sparse Matrix of class "dgCMatrix"
#> [[ suppressing 12 column names 'A.A.A.A.A_0.0.0.0', 'A.V.V.A.V_0.0.0.0', 'V.V.A.V.F_0.0.0.0' ... ]]
#>
#> [1,] 1 1 1 1 1 1 1 . . . . .
#> [2,] . . . . . . . 1 1 1 2 1count_kmers(sequences=c("AAAAAVVAVFF", "DFGSADFGSA"),
kmer_gaps=c(0, 1, 0, 2))
#> 2 x 7 sparse Matrix of class "dgCMatrix"
#> A.A.A.A.A_0.1.0.2 A.A.V.V.F_0.1.0.2 A.A.V.A.F_0.1.0.2 A.A.A.V.V_0.1.0.2
#> [1,] 1 1 1 1
#> [2,] . . . .
#> G.S.D.F.A_0.1.0.2 F.G.A.D.S_0.1.0.2 D.F.S.A.G_0.1.0.2
#> [1,] . . .
#> [2,] 1 1 1data(CsgA)
CsgA[1L:2]
#> $`sp|P28307|CSGA_ECOLI Major curlin subunit OS=Escherichia coli (strain K12) OX=83333 GN=csgA PE=1 SV=3`
#> [1] "M" "K" "L" "L" "K" "V" "A" "A" "I" "A" "A" "I" "V" "F" "S" "G" "S" "A"
#> [19] "L" "A" "G" "V" "V" "P" "Q" "Y" "G" "G" "G" "G" "N" "H" "G" "G" "G" "G"
#> [37] "N" "N" "S" "G" "P" "N" "S" "E" "L" "N" "I" "Y" "Q" "Y" "G" "G" "G" "N"
#> [55] "S" "A" "L" "A" "L" "Q" "T" "D" "A" "R" "N" "S" "D" "L" "T" "I" "T" "Q"
#> [73] "H" "G" "G" "G" "N" "G" "A" "D" "V" "G" "Q" "G" "S" "D" "D" "S" "S" "I"
#> [91] "D" "L" "T" "Q" "R" "G" "F" "G" "N" "S" "A" "T" "L" "D" "Q" "W" "N" "G"
#> [109] "K" "N" "S" "E" "M" "T" "V" "K" "Q" "F" "G" "G" "G" "N" "G" "A" "A" "V"
#> [127] "D" "Q" "T" "A" "S" "N" "S" "S" "V" "N" "V" "T" "Q" "V" "G" "F" "G" "N"
#> [145] "N" "A" "T" "A" "H" "Q" "Y"
#>
#> $`sp|P0A1E7|CSGA_SALEN Major curlin subunit OS=Salmonella enteritidis OX=149539 GN=csgA PE=1 SV=1`
#> [1] "M" "K" "L" "L" "K" "V" "A" "A" "F" "A" "A" "I" "V" "V" "S" "G" "S" "A"
#> [19] "L" "A" "G" "V" "V" "P" "Q" "W" "G" "G" "G" "G" "N" "H" "N" "G" "G" "G"
#> [37] "N" "S" "S" "G" "P" "D" "S" "T" "L" "S" "I" "Y" "Q" "Y" "G" "S" "A" "N"
#> [55] "A" "A" "L" "A" "L" "Q" "S" "D" "A" "R" "K" "S" "E" "T" "T" "I" "T" "Q"
#> [73] "S" "G" "Y" "G" "N" "G" "A" "D" "V" "G" "Q" "G" "A" "D" "N" "S" "T" "I"
#> [91] "E" "L" "T" "Q" "N" "G" "F" "R" "N" "N" "A" "T" "I" "D" "Q" "W" "N" "A"
#> [109] "K" "N" "S" "D" "I" "T" "V" "G" "Q" "Y" "G" "G" "N" "N" "A" "A" "L" "V"
#> [127] "N" "Q" "T" "A" "S" "D" "S" "S" "V" "M" "V" "R" "Q" "V" "G" "F" "G" "N"
#> [145] "N" "A" "T" "A" "N" "Q" "Y"
count_multimers(sequences=CsgA,
k_vector = c(1, 2))
#> 5 x 144 sparse Matrix of class "dgCMatrix"
#> [[ suppressing 144 column names 'R', 'L', 'Y' ... ]]
#>
#> [1,] 2 9 4 1 8 5 10 2 2 4 16 29 4 11 9 2 16 3 14 1 2 1 1 1 1 2 1 1 1 1 1 3 1 2
#> [2,] 3 8 5 2 7 6 11 2 2 4 17 22 3 11 10 2 20 1 15 1 3 1 . . 3 1 1 1 2 5 2 3 . 2
#> [3,] 3 8 5 2 7 6 11 2 2 4 17 22 3 11 10 2 20 1 15 1 3 1 . . 3 1 1 1 2 5 2 3 . 2
#> [4,] 2 9 4 1 9 5 10 2 1 4 15 30 4 11 9 2 17 4 13 1 2 1 1 1 1 2 1 1 1 1 1 3 1 2
#> [5,] 3 8 5 2 7 6 11 2 2 4 17 22 3 11 10 2 20 1 15 1 3 1 . . 3 1 1 1 2 5 2 3 . 2
#>
#> [1,] 1 3 1 3 1 2 7 1 1 1 1 3 1 1 2 2 1 1 12 3 1 2 1 1 1 1 1 1 1 1 1 1 1 2 1 2 2
#> [2,] . 2 . 2 1 2 3 . 1 2 . 3 1 . 3 2 2 1 6 4 2 3 1 2 1 . 1 . 1 1 . 1 . 1 1 2 .
#> [3,] . 2 . 2 1 2 3 . 1 2 . 3 1 . 3 2 2 1 6 4 2 3 1 2 1 . 1 . 1 1 . 1 . 1 1 2 .
#> [4,] 1 3 1 3 1 2 6 1 1 2 1 3 2 1 2 2 1 . 13 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2
#> [5,] . 2 . 2 1 2 3 . 1 2 . 3 1 . 3 2 2 1 6 4 2 3 1 2 1 . 1 . 1 1 . 1 . 1 1 2 .
#>
#> [1,] 1 1 1 1 1 1 2 7 1 1 2 1 1 1 2 1 1 1 1 1 1 2 2 3 1 1 1 1 1 1 1 2 2 1 1 3 1
#> [2,] . 1 . 1 1 1 1 5 . . 2 . . 1 1 1 . . . 1 1 2 1 4 1 1 1 1 . 1 . 2 3 1 1 1 .
#> [3,] . 1 . 1 1 1 1 5 . . 2 . . 1 1 1 . . . 1 1 2 1 4 1 1 1 1 . 1 . 2 3 1 1 1 .
#> [4,] 1 1 . 1 1 1 1 7 1 1 2 1 1 1 2 1 . 1 1 1 1 2 2 3 1 . 1 1 1 1 1 1 2 1 1 3 1
#> [5,] . 1 . 1 1 1 1 5 . . 2 . . 1 1 1 . . . 1 1 2 1 4 1 1 1 1 . 1 . 2 3 1 1 1 .
#>
#> [1,] 1 1 2 1 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
#> [2,] . 1 . 1 3 1 1 1 1 1 1 1 1 1 1 2 1 1 2 2 1 1 1 2 1 1 1 1 1 1 1 1 . . . .
#> [3,] . 1 . 1 3 1 1 1 1 1 1 1 1 1 1 2 1 1 2 2 1 1 1 2 1 1 1 1 1 1 1 1 . . . .
#> [4,] 1 1 2 1 2 . . . . . . . . . . . . . 1 . . . . . . . . . . . . . 1 1 1 1
#> [5,] . 1 . 1 3 1 1 1 1 1 1 1 1 1 1 2 1 1 2 2 1 1 1 2 1 1 1 1 1 1 1 1 . . . .For citation type:
citation("seqR")or use:
Jadwiga Słowik and Michał Burdukiewicz (2021). seqR: fast and comprehensive k-mer counting package. R package version 1.0.0.
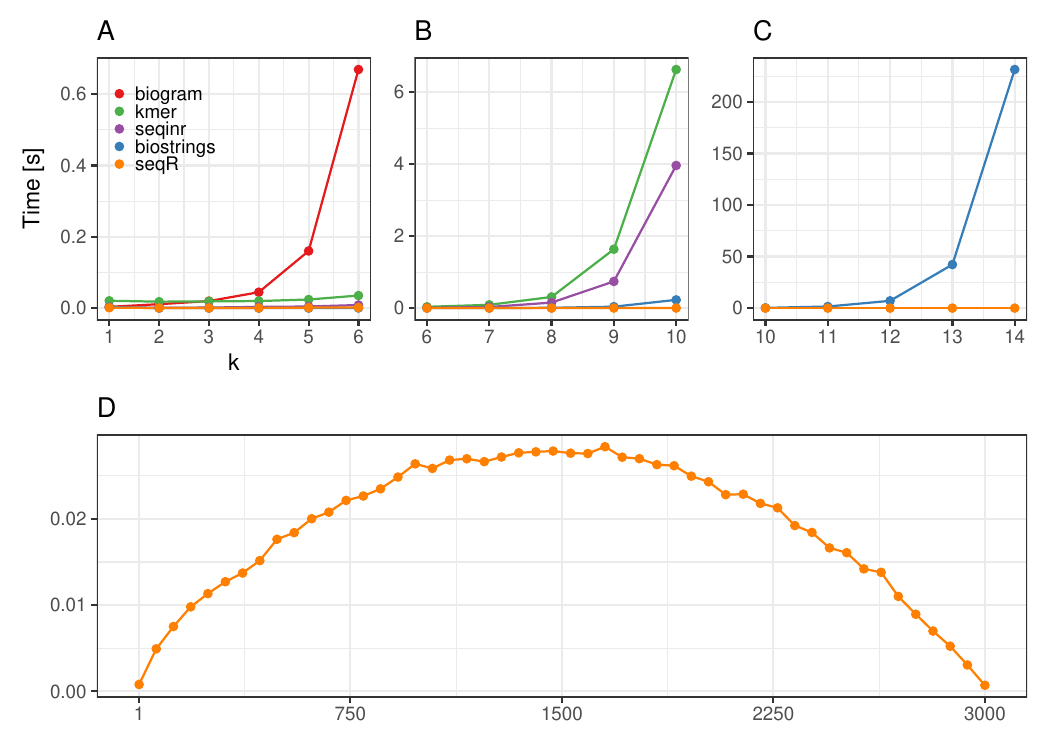
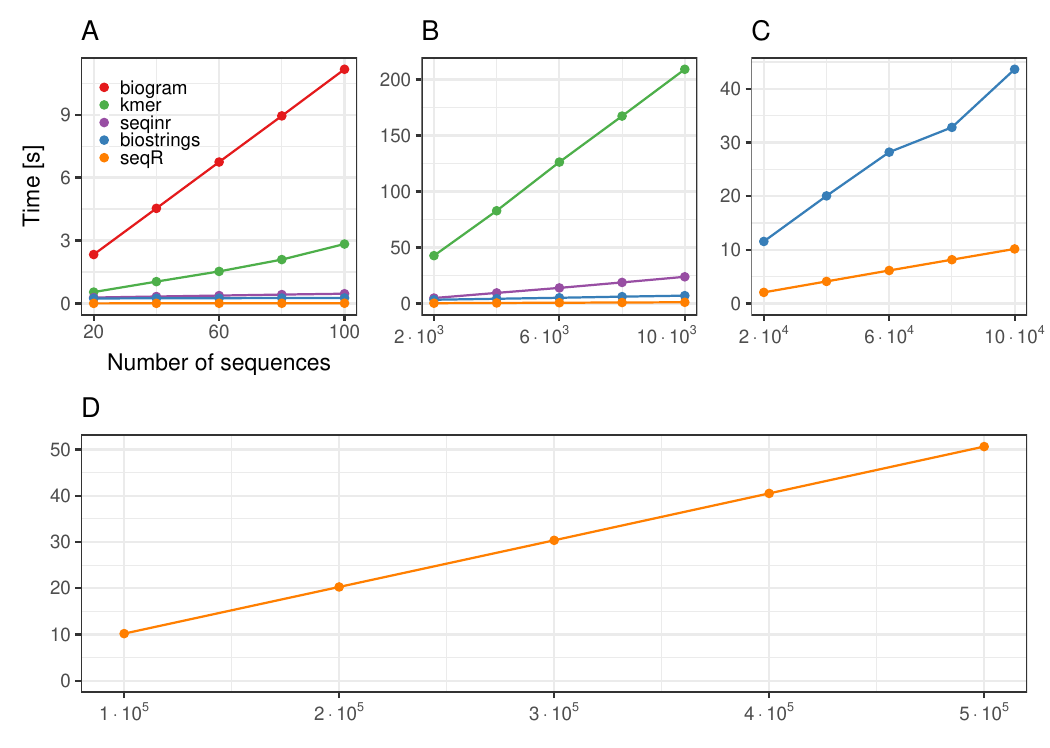
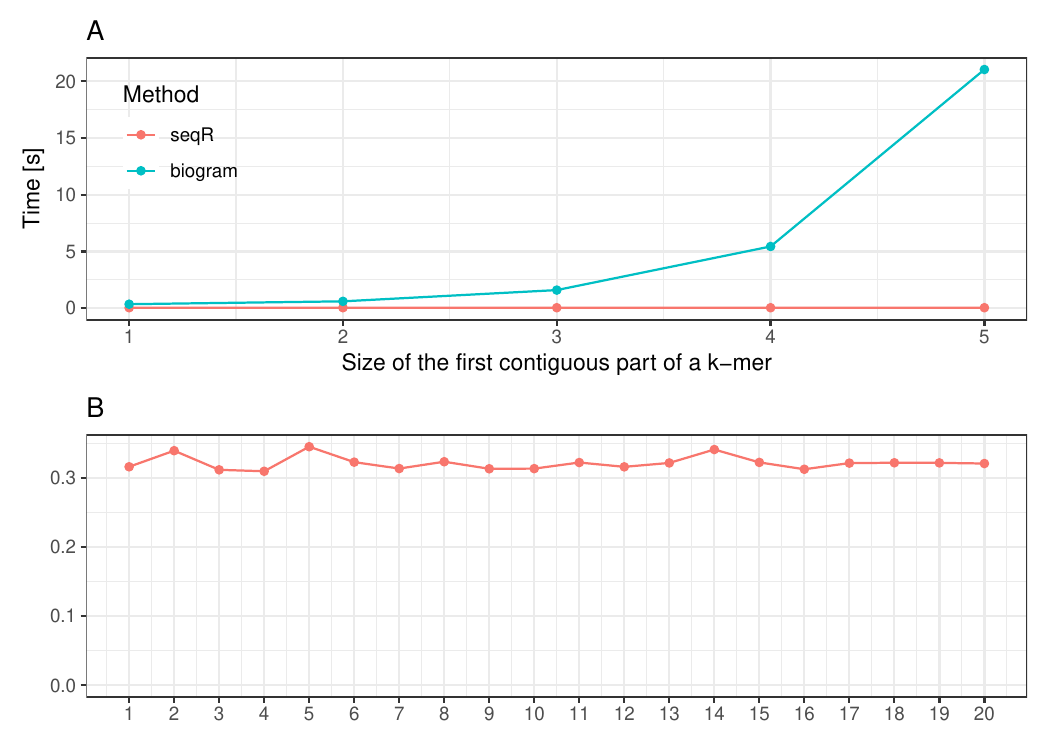
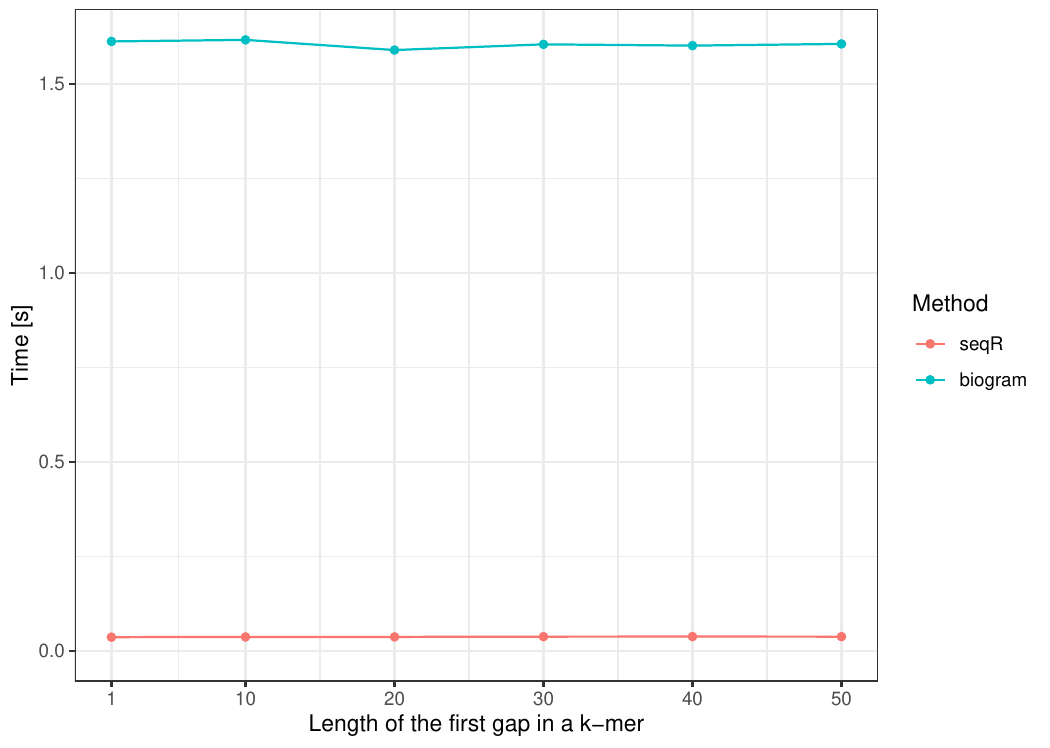
The seqR package has been compared with other existing k-mer counting
R packages: biogram,
kmer,
seqinr, and
biostrings.
All benchmark experiments have been performed using Intel Core i7-6700HQ 2.60GHz 8 cores, using the microbenchmark R package.
The input consists of one DNA sequence of length 3 000.
Each DNA sequence has 3 000 elements, contiguous 5-mer counting.
The input consists of one DNA sequence of length 1 000 000.
Gapped 5-mers counting with base gaps (1, 0, 0, 1).
The input consists of one DNA sequence of length 100 000.
Gapped 5-mers counting with base gaps (1, 0, 0, 1).