-
Notifications
You must be signed in to change notification settings - Fork 41
ShadowBias
在先前的ShadowMap实现中,已经简单的提到了shadow bias。可参考如下: 平行光实时阴影
当时只实现了一个简单的版本:
Bias的问题,目前是直接取了Light组件的设置,更好的方式是要结合ShadowMap分辨率来计算恰当的偏移。
本篇准备详细的展开聊聊shadow bias,以及实际实现中的自适应优化算法。将会包含以下内容:
- 阴影瑕疵(shadow acne)的成因及其数学模型
- shadow bias数值的精确计算方法
- 级联阴影(cascade shadow)对shadow bias的影响
- PCF阴影对shadow bias的影响
- 两种不同的shadow bias实现方式
- 自适应的bias算法
shadow bias是为了解决自遮挡阴影瑕疵(shadow acne)而提出的。 由于shadowmap技术自身的原因,当bias没有加入时,场景中会出现条状阴影纹路,这便是自遮挡阴影瑕疵。

引起shadow acne的原因如下:
- ShadowMap的分辨率有限
- 因此ShadowMap中的一个像素,对应到场景上是一片区域。
- 在ShadowMap生成阶段(Shadow Caster),该区域内的点(假设都暴露在光照下)最终会汇集到ShadowMap上的一个像素,形成一个平均深度值D。
- 在阴影计算阶段(Shadow Receiver),当我们将该区域内的点投影到ShadowMap中进行深度对比时,会发现其中一些点的深度大于D,而其中一些小于D,因此形成了亮暗条纹。
用一张图来解释:
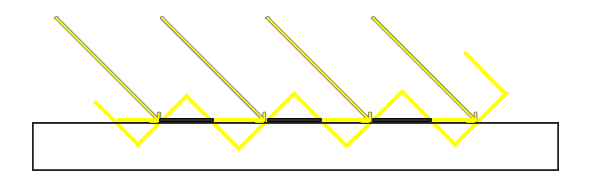
箭头为入射的平行光,每一条斜黄线断代表ShadowMap贴图中的一个像素,对应到水平地面上可能覆盖多个像素。多个像素里有些深度较大,有些深度较小,因而产生了条状瑕疵。
我们可以使用一个Shadow Debug Pass,将ShadowMap的分辨率以红黑格子的形式,投影到场景中绘制出来如下:

可以看得出来,自遮挡引起的阴影瑕疵条纹与shadowmap的分辨率格子大小是一致的。
凑近了观察一下

红黑格子为shadowmap投下的分辨率(平行光以45度照射,因此格子呈现1:2的长方形)。黑白条纹会自遮挡引起的阴影瑕疵。我们可以看出,从左至右,一个分辨率格子内包含了黑白条纹各一条。
接下来我们会将以上的阴影自遮挡问题,转化为一个纯粹的几何问题,来用数学进行精确描述。这将解释:
- 为什么瑕疵条纹与ShadowMap的分辨率会呈现以上的关系
- 如何精确的计算Bias的数值来修正自遮挡问题。
首先看下图:

- 橙色线条为平行光视角的近平面,记为L,这个近平面最终将映射为一张ShadowMap深度图。
- 蓝色线条为接受光照的平面。
我们暂且假设Light对应的正交矩阵其宽高相同(实际上URP中就是这样的),记为frustumSize。ShadowMap贴图的尺寸记为shadowMapSize。
设AB代表ShadowMap贴图上单位像素在Light近平面上对应的尺寸。那么我们有以下公式:
|AB| = frustumSize / shadowMapSize
从AB作橙线的垂线,相交场景蓝色平面于CD两点。易知,CD范围内的所有像素均投影到平面L上的AB区域。
由于AB代表了ShadowMap上的单个像素,因此AB像素中存储的深度值应当是CD中点F到平面L的距离,即|FE|(实际上是归一的)。
我们记:
Distance(X,L) - 表示任意点X到光源近平面L的距离。
那么显然:
- 对任意点X属于CF,有Distance(X,L) < |FE|,因此判定为不在阴影中
- 对任意点X属于DF,有Distance(X,L) > |FE|,因此判定为在阴影。
于是在CD区域中会呈现出一半白,一半黑的阴影瑕疵,这就是Shadow Acne,其以CD长度为周期在平面上循环交替,而|CD|正是ShadowMap中单个像素投射在场景上覆盖的区域。
既然已经知道了问题所在,我们就可以在深度对比阶段,来修正这个问题。
过F点做L的平行线p,如下图:

我们只要将CD中的点,往光照方向平移一定距离到GH上即可修正误差。这个移动的距离即称为Depth Bias。不妨先考察D点。 |DG|即是要修正的Depth Bias,于是我们有:
那么对于CD上的任意点X,我们可以使用相似三角形的原理,从DepthBias(D)乘以对应的比例就可以了。
伪代码如下:
shadowUV = shadowProj(X);
percent = (frac(shadowUV) - 0.5) / 0.5;
DepthBias_X = DepthBias_D * percent;
实际上在大多数引擎的实现中,并不会这么精确的去计算每个点的bias数值,而是对所有的点执行一个固定的Depth Bias。很明显,D点的误差是最大的,因此只要对所有的点都使用D点的bias数值,就可以修正自遮挡的问题。
但是固定的depth bias也会引起其他的问题。
考虑点C前面有个遮挡物。
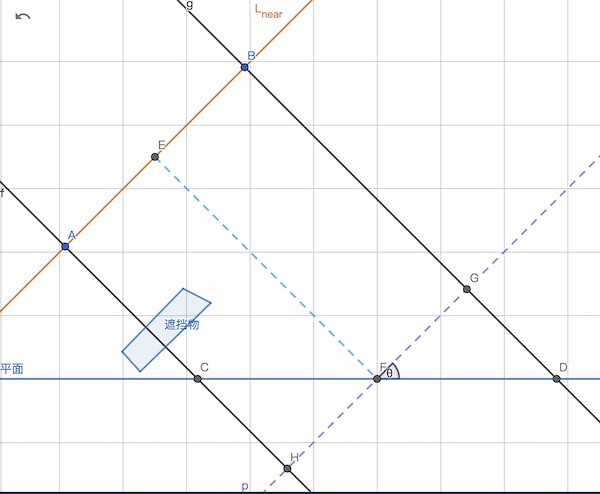
本来C点应该是处于阴影中的。但是我们通过depth bias将C点往光源方向进行了长度为|DG|的偏移,那么C点就变到了遮挡物前面去了。这就是固定depth bias引起的漏光现象。
当入射光线与平面夹角趋于0,即$\theta$趋于90度时,线段DG长度会趋于无穷大。从|DG|的公式也可以看出:
如下图:过大的depth bias引起漏光问题

为了解决Depth Bias的缺陷,于是人们提出了Normal Bias。顾名思义,既然往光源方向偏移有问题,那么我就往法线方向偏移呗。
如下图所示:

将CD平面按照法线方向,平移到C'D',平移距离为G到CD的距离即|GM|。从图中可以看出,经过法线方向平移后:
- C'G段的点,深度均小于|EF|,因此光亮
- D'G段的点,移动到了隔壁的像素区间,易知也是小于隔壁像素深度的,同样呈现光亮。
这样同样可以解决shadow acne。通过简单的几何知识,我们可以写出关于Normal Bias的公式,即对任意点X属于CD有:
$$ \begin{aligned} NormalBias(X) &= |GM| \ &= |GF| * \sin(\theta) \ &= \frac{frustumSize * \sin(\theta)}{shadowMapSize * 2} \end{aligned}
$$
于Depth Bias相比,其优点在于当$\theta$趋于90度时,bias趋于{frustumSize/(2 * shadowMapSize)},而不是无穷大。也即,normal bias的最大值只与shadowMap的分辨率有关。
Normal Bias同样会存在漏光问题,并且是两头漏光。考虑有个遮挡物如下:

该遮挡本应该在CD区域投下阴影。但由于normal bias的存在,我们在进行深度判定的时候将CD移到了C'D',因此CD平面左侧会有少部分位于遮挡物上方,从而漏光。而右侧的GD'部分,也因为进入了隔壁的像素地盘,形成了漏光。
但在实际应用中,由于Normal Bias的最大值相对可控(只要提升ShadowMap分辨率即可),因此漏光问题并不太严重。
根据前面推导的公式,我们已知影响最大Bias的两个因素如下:
- ShadowMap的分辨率
- 平行光的入射角
级联阴影的策略是将摄像机视锥按照不同的距离区间划分成多块,每块使用不同分辨率的ShadowMap,称为一级。因此,在使用级联阴影时,如要计算场景中某个点的Bias,必须考虑到它属于哪一级别(cascadeIndex),计算出该级别的ShadowMap分辨率,然后再根据分辨率求Bias。
看下图:

在开启4级CSM的情况下,由近及远,由于每级ShadowMap分辨率不一样,因此自遮挡引起的条纹也呈现出不同的分布密度。假如我们对整个场景都使用相同的bias而没有针对CSM每个级别单独计算,那么会出现以下情况:

近处的瑕疵消失了,但远处依旧会出现。如若我们为了照顾最远级别的CSM而将Bias调的很大,那么近处的漏光现象就会变得严重。
因此自适应的Bias算法需要考虑场景像素所在的CSM级别,并按照相应的CSM分辨率进行计算。
PCF会采样一个范围内的像素,因此我们必须考虑这个范围内距离光源最近的那个像素。
例如对于PCF1,它会采样ShadowMap上的4个像素,依次进行深度对比测试。
如下图:
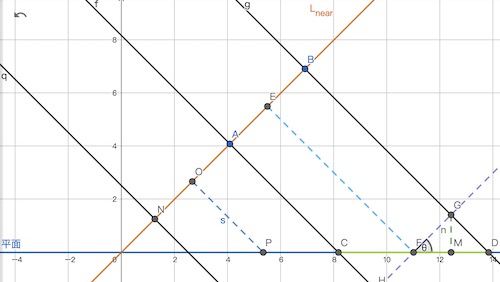
当我们计算CF区间内的像素阴影时,除了会采样AB对应的ShadowMap像素,同时还会采样到AN对应的ShadowMap像素。
此时,取|GD|作为Depth Bias已无法满足要求。根据相似三角形原理易知,只有将Depth Bias取为2 * |GD|,才能令CF内的所有点到L的距离小于|OP|,从而修正acne。
易知,该推导可以扩展到任意采样半径R。即:
- ceil为向上取整函数
同样的,对于Normal Bias我们也可以推出其满足这个比例系数,即:
以上我们提到的Bias,都是默认发生在Shadow Receive计算阶段,并且是Per Pixel的。这时候就有人提出,那我可不可以反过来,在Shadow Caster阶段,让遮蔽物进行反向偏移呢? 不得不说,这个逆向思维非常好。这就是Shadow Caster阶段基于顶点的Bias,我们不妨称之为SCVBB(ShadowCaster Vertex Based Bias) - 这也是URP中采用的实现方式。我们可以看下Unity文档中的说明:
Light.shadowBias(即depth bias)
Shadow caster surfaces are pushed by this world-space amount away from the light, to help prevent self-shadowing ("shadow acne") artifacts.
Shadow caster surfaces are pushed inwards along their normals by this amount, to help prevent self-shadowing ("shadow acne") artifacts. Units of normal-based bias are expressed in terms of shadowmap texel size; typically values between 0.3-0.7 work well.
下面我们来分析一下SCVBB的优缺点。
优点自然是计算廉价,因为是基于顶点的。而缺点有两个。
其一是偏移精度的问题。我们知道,Bias的值与光线和法线夹角相关。SCVBB只考虑顶点处的法线,因此在整体偏移上可能会存在一定误差,不过这个误差在大多数情况下都还好。
另一个缺点比较严重,即Caster阶段的反向Normal Bias不完全等价于Receive阶段的Normal Bias。
考虑如下一种情形:

因为ShadowMap精度问题,AH区域会呈现出阴影(被AB区域在Caster阶段写入的深度所遮挡)。
假如我们在Receive阶段进行Normal Bias,那么AH会往法线方向平移到A'H',从而消除阴影。
但是假如在Caster阶段进行反向Normal Bias,那么AB面需要向右移动超过H的位置,才能不对AH形成遮挡。当光线入射角度与AD接近于平行时,这个移动距离将趋于无穷大,因而导致瑕疵无法再被消除。这个情况在我们使用了PCF软阴影后,将会变得更加明显。
各位不妨在URP管线中试验一下,开启软阴影,然后让平行光以接近水平的方式照射一个Cube,将会呈现出如下效果:

以上测试效果图使用的参数是:
- Distance 10
- 关闭Cascades
- 开启Soft Shadows
- Directional Light Rotation = (2,30,0)
可以看到顶部出现了如我们预测的阴影瑕疵。这里尝试将Depth Bias和Normal Bias均调到了最大值,依旧无法消除瑕疵(瑕疵仅向内部进行了移位),并且底部出现了漏光。
我的疑问是,仅仅为了Fragment阶段省下这么一点Bias计算量,而采用Shadow Caster Bias,值得吗?
在实际的实现中,为了避免三角函数运算,通常可以使用 1 - dot(lightDir,normal)来近似代替tan和sin,然后暴露出两个系数$C_{depth}$ 和$C_{normal}$,给予使用者进行调整。
于是bias的公式就变成如下形式:
$$
\begin{aligned}
&A = (1 + ceil(R)) * \frac{frustumSize}{shadowMapSize * 2} \ &B = 1 - dot(lightDir,normal) \ &DepthBias = C_{depth} * A * B \ &NormalBias = C_{normal} * A * B
\end{aligned}
$$
其中A可以在CPU端完成计算,以上的实现在大多数情况下都可以取得不错的效果。