-
Notifications
You must be signed in to change notification settings - Fork 266
Symmetric Tree
- 🔗 Leetcode Link: Symmetric Tree
- 💡 Problem Difficulty: Easy
- ⏰ Time to complete: 15 mins
- 🛠️ Topics: Binary Trees, Depth First Search, Breadth First Search
- 🗒️ Similar Questions: Leaf-Similar Trees, Invert Binary Tree, Same Trees
Understand what the interviewer is asking for by using test cases and questions about the problem.
- Established a set (2-3) of test cases to verify their own solution later.
- Established a set (1-2) of edge cases to verify their solution handles complexities.
- Have fully understood the problem and have no clarifying questions.
- Have you verified any Time/Space Constraints for this problem?
- What is the type of tree we are working with?
- The input tree will be a binary tree
- Can I assume the tree will be complete?
- No. A node may have less than 2 children
- Can I expect to receive an empty tree as input?
- No, the input tree can have 1-1000 nodes.
HAPPY CASE
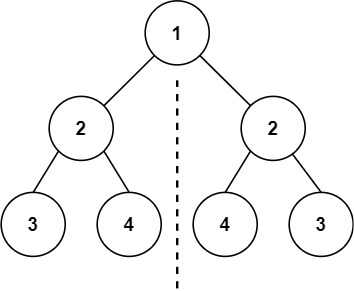
Input: root = [1,2,2,3,4,4,3]
Output: trueInput: root = [1,2,2,null,3,null,3]
Output: falseEDGE CASE
Input: root = []
Output: trueMatch what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.
If you are dealing with Binary Trees some common techniques you can employ to help you solve the problem:
- Think about appropriate Tree Traversal: Pre-Order, In-Order, Post-Order, Level-Order
- Since we need to compare nodes and node values in both trees top down, a Pre-Order traversal would be appropriate
- Store nodes within a HashMap to refer to later
- We don't need to access the nodes or their values after they have been processed, so this technique is not useful for this problem
- Using Binary Search to find an element
- We are not looking to find an element in this problem so this technique is not useful for this problem
- Applying a level-order traversal with a queue
- Since we need to compare nodes and node values in both trees top down, a level-order traversal using a queue would be appropriate
Plan the solution with appropriate visualizations and pseudocode.
General Idea: Recursively traverse both trees using Pre-Order traversal and check if each node is equal to the other.
1. Create isSameTree recursive function to traverse left and right child of root and check for symmetry.
a. Basecase: If both left and right child is None, then return True
b. If both left and right child are equal, then continue to check symmetry
c. Otherwise return False
2. If there is no root, then return True
3. Set left child as left tree and right child as right tree
4. Return isSameTree recursive function on the two trees. - Choosing the wrong traversal type
- Try to walk through the problem by hand and see the order in which you are processing the nodes. This will clue you into the type of traversal necessary
- Suppose you choose post order traversal, we would go left - right - check. Slower, no early exit
- Suppose you choose in order traversal, we would go left - check - right. Slower, no early exit
Implement the code to solve the algorithm.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
# Create isSameTree recursive function to traverse left and right child of root and check for symmetry
def isSameTree(p:Optional[TreeNode], q:Optional[TreeNode]) -> bool:
# Basecase: If both left and right child is None, then return True
if not p and not q:
return True
# If both left and right child are equal, then continue to check symmetry
if p and q and p.val == q.val:
return isSameTree(p.left, q.right) and isSameTree(p.right, q.left)
else:
# Otherwise return False
return False
# If there is no root, then return True
if not root:
return True
# Set left child as left tree and right child as right tree
p = root.left
q = root.right
# Return isSameTree recursive function on the two trees
return isSameTree(p,q)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
// If there is no root, then return True and
// Return isSameTree recursive function on the two trees
return root==null || isSymmetricHelp(root.left, root.right);
}
// Create isSameTree recursive function to traverse left and right child of root and check for symmetry
private boolean isSymmetricHelp(TreeNode left, TreeNode right){
// Basecase: If both left and right child is None, then return True
if(left==null && right==null)
return true;
// If both left and right child are equal, then continue to check symmetry
if(left!=null && right!=null && left.val==right.val)
return isSymmetricHelp(left.left, right.right) && isSymmetricHelp(left.right, right.left);
// Otherwise return False
return false;
}
}Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.
- Trace through your code with an input to check for the expected output
- Catch possible edge cases and off-by-one errors
Evaluate the performance of your algorithm and state any strong/weak or future potential work.
Assume N represents the number of nodes in binary tree
-
Time Complexity:
O(N)- We need to visit each node in the binary tree
-
Space Complexity:
O(N)because unbalanced tree (space is used for the recursion stack). In the general case O(logN) for balanced tree.