-
Notifications
You must be signed in to change notification settings - Fork 266
Transpose Matrix
- 🔗 Leetcode Link: Transpose Matrix
- 💡 Problem Difficulty: Easy
- ⏰ Time to complete: 15 mins
- 🛠️ Topics: Array, 2D-Array
- 🗒️ Similar Questions: Flipping an Image, Rotate Image
Understand what the interviewer is asking for by using test cases and questions about the problem.
- Established a set (2-3) of test cases to verify their own solution later.
- Established a set (1-2) of edge cases to verify their solution handles complexities.
- Have fully understood the problem and have no clarifying questions.
- Have you verified any Time/Space Constraints for this problem?
- Can the input grid be blank??
- Let’s assume the grid is not blank. We don’t need to consider empty inputs.
- Can the row size be different from the column size?
- Yes, the row size can be different from the column size.
- What are the time and space constraints?
- Time complexity should be
O(m*n), m being the rows of the matrix and n being the columns of matrix. Space complexity should beO(m*n)too.
- Time complexity should be
HAPPY CASE
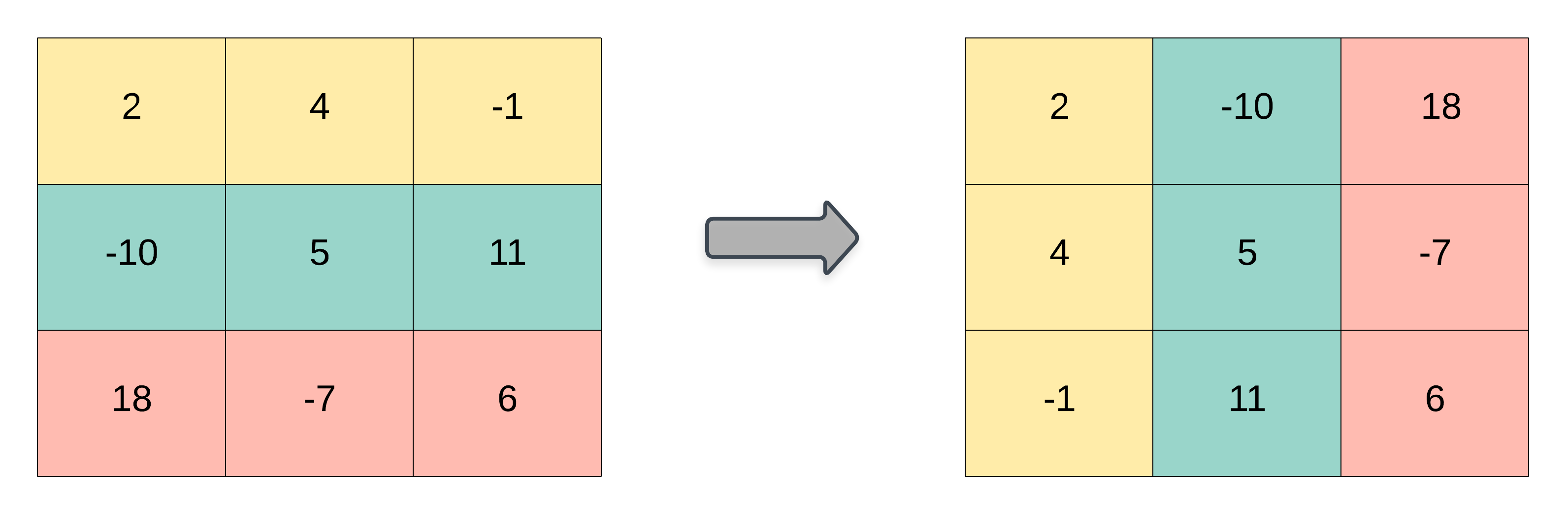
Input: matrix = [[2,4,-1],[-10,5,11],[18,-7,6]]
Output: [[2,-10,18],[4,5,-7],[-1,11,6]]Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[1,4,7],[2,5,8],[3,6,9]]
EDGE CASE
Input: matrix = [[1]]
Output: [[1]]Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.
For 2D-Array, common solution patterns include:
- Perform a BFS/DFS Search through the 2D Array
- A search through the 2D Array (either BFS or DFS) does not help us. We are transposing, not searching.
- Hash the 2D Array in some way to help with the Strings
- Hashing would not help us transpose this array
- Create/Utilize a Trie
- A Trie would not help us much in this problem since we are not trying to determine anything about a sequence of characters.
Plan the solution with appropriate visualizations and pseudocode.
Solution 1:
General Idea: Use a zip function to gather all the first elements together and form a group, and so forth. i.e. [1, 2, 3] and [10, 20, 30] and returns (1, 10), (2, 20), (3, 30)
Use zip function on the unpacked matrix array, to gather the first elements together and form a group and so forth. Solution 2:
General Idea: Use list comprehension to access the column, to gather elements in row by column
Use list comprehension to access the column, to gather elements in row by columnSolution 3:
General Idea: Create row from each column and fill each row with each column
1) Create empty array
2) Create row for each column
3) Get each element from same column and insert into row
4) Return result- Not every 2D-Array problem follows the common techniques.
Implement the code to solve the algorithm.
Solution 1:
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
# Use zip function on the unpacked matrix array, to gather the first elements together and form a group and so forth.
return zip(*matrix)Solution 2:
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
# Use list comprehesion to access the column, to gather elements in row by column
return [[matrix[i][j] for i in range(len(matrix))] for j in range(len(matrix[0]))]Solution 3:
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
# Create empty array
result = []
# Create row for each column
for j in range(len(matrix[0])):
result.append([])
# Get each element from same column and insert into row
for i in range(len(matrix)):
result[j].append(matrix[i][j])
# Return result
return resultclass Solution {
public int[][] transpose(int[][] A) {
//Create empty array
int M = A.length; int N = A[0].length;
int[][] B = new int[N][M];
// Create row for each column
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
// Get each element from same column and insert into row
B[j][i] = A[i][j];
}
}
// Return result
return B;
}
}Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.
- Trace through your code with an input to check for the expected output
- Catch possible edge cases and off-by-one errors
Evaluate the performance of your algorithm and state any strong/weak or future potential work.
Assume N represents the number of rows in 2D-array.
Assume M represents the number of columns in 2D-array.
All 3 solutions results in the same space and time complexity
- Time Complexity: O(N * M) we need to view each item in the 2D-Array
- Space Complexity: O(N * M), because we need space to hold the resulting matrix